Расчет индуктивности цепи выпрямленного тока

Принятое ранее допущение, что выпрямленный ток идеально сглажен, справедливо при индуктивности цепи нагрузки L_d, стремящейся к бесконечности. При реальных конечных значениях L_d выпрямленный ток пульсирует от значения I_{d min} до значения I_{d max} с такой же частотой, как и выпрямленное напряжение. Пульсации выпрямленного тока характеризуются коэффициентом пульсаций

,

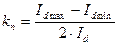где I_d – среднее значение тока.

Точное значение k_п можно определить, разлагая I_d в ряд Фурье и суммируя гармонические составляющие с учетом угла сдвига фаз между ними. Приемлемую погрешность дает расчет k_п с учетом только первой гармоники тока

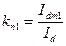, (26)

где I_dm1 – амплитудное значение первой гармонической составляющей выпрямленного тока.

Для обеспечения требуемого значения коэффициента пульсаций (в цепи тягового двигателя максимально допустимое значение k_п составляет 0,25-0,3) последовательно с двигателем включается дроссель, который называют сглаживающим реактором. Индуктивность дросселя L_др и индуктивность двигателя L_дв в сумме дают индуктивность цепи нагрузки

L_d = L_др + L_дв.

Связь между k_п и L_d устанавливается из эквивалентной схемы цепи нагрузки выпрямителя, приведенной на рис.8 а. Активное сопротивление цепи нагрузки на схеме не показано, так как оно принято равным нулю. Кроме этого, при расчетах принимается, что показанная на схеме ЭДС E, возникающая в якоре при его вращении, не имеет пульсаций и равна среднему значению выпрямленного напряжения U_d. Допущение это правомерно, так как пульсации тока в обмотке возбуждения ОВ значительно меньше, чем пульсации тока якоря. Для этого обмотка возбуждения зашунтирована резистором R_ш, сопротивление которого значительно меньше полного сопротивления обмотки возбуждения. В результате основная часть переменной составляющей i_d проходит через R_ш, минуя обмотку возбуждения.

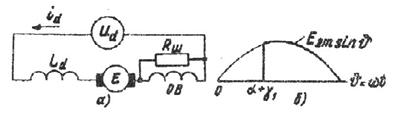
Рис.8

Условие U_d = E означает, что переменная составляющая выпрямленного напряжения равна напряжению на индуктивном сопротивлении X_d. При этом амплитудное значение первой гармонической составляющей тока равно

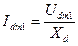, (27)

где U_dm1 – амплитудное значение первой гармонической составляющей выпрямленного напряжения.

Разложение u_d в ряд Фурье дает, что первая (низшая) гармоническая составляющая u_d имеет частоту, в два раза превышающую частоту сети f_с. Значение Xd на этой частоте

X_d = 4·π·f_c·L_d. (28)

Из выражений (26)-(28) получаем формулу для расчета индуктивности L_d, обеспечивающей заданное значение k_п1,

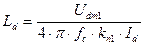. (29)

4.1) Амплитудное значение первой гармонической составляющей выпрямленного напряжения.

Расчет ведется для значения α + γ₁, равного заданному расчетному значению угла регулирования α_р = α+γ₁= 0,733 рад.

Для расчета U_dm1 определяются коэффициенты ряда Фурье a_n, b_n при n=1:

;

;

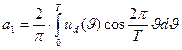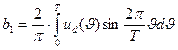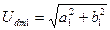. (30)

В соответствии с рис.8 б период Т функции u_d(υ) равен π. С учетом того, что в интервале от α+γ₁ до π u_d=E_2msinυ, получаем:

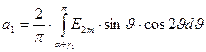; (31)

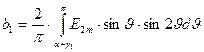. (32)

Получаем

;

.

;

.

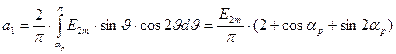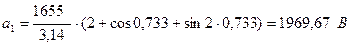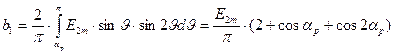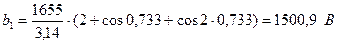Рассчитаем амплитудное значение первой гармонической составляющей выпрямленного напряжения.

.

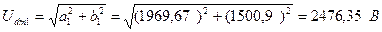4.2) Индуктивность цепи выпрямленного тока.

Расчет ведется для заданного значения k_п1 = 0,21 и I_d = I_dн = 1250 А.

Индуктивность цепи выпрямленного тока по (29) равна

.
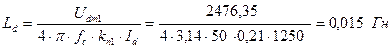