Электромагнитный переходный процесс

В ЭЛЕКТРИЧЕСКИХ МАШИНАХ

Аналитическое исследование электромагнитного переходного процесса в электрических машинах представляет достаточно сложную задачу. Для упрощения её решения вводится ряд допущений:

· учитывается только периодическая слагающая тока статора;

· скорость ротора считается неизменной и равной ;

· рассматривается синхронная машина, работающая отдельно от других источников питания;

· предполагается, что машина работает в линейном режиме (что позволяет при анализе переходных процессов использовать метод наложения).

Таким образом, в дальнейшем рассматривается в известной мере идеализированная машина. Это вносит погрешности в оценку отдельных величин. Однако, как показывают сопоставления полученных величин с экспериментальными данными, обычно погрешности находятся в допустимых для практических расчётов пределах.

Уравнения синхронной машины в фазных координатах

Принципиальная схема синхронной машины, ротор которой имеет явновыраженные полюсы, представлена на рис.6.1. Первоначально предположим, что синхронная машина не имеет демпферных обмоток.

Рис.6.1. Принципиальная схема явнополюсной синхронной машины

Дифференциальные уравнения для каждой из обмоток синхронной машины

, (6.1)

где - активные сопротивления контуров каждой фазы цепи возбуждения соответственно, - результирующие потокосцепления обмоток статора и обмотки возбуждения соответственно, - напряжения на зажимах соответствующих обмоток.

При принятых допущениях выражения для потокосцеплений представляют линейные зависимости. Так для потокосцепления фазы

,

где - индуктивность фазы 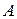; - взаимные индуктивности фазы 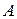с фазам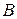и и 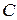и обмоткой возбуждения (индекс 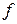) соответственно.

Аналогично

,

где - индуктивность обмотки возбуждения. Необходимо отметить, что по принципу взаимности , и т.д.

Параметры L и M зависят от положения ротора относительно обмоток статора и, следовательно, являются функциями времени. Только индуктивность обмотки возбуждения можно считать неизменной. Положение ротора будем характеризовать углом между магнитной осью фазы А и продольной осью (рис.6.2).

Рис.6.2. К определению пространственного положения ротора

Синусоидальность наводимых в статоре ЭДС указывает на гармонический закон изменения взаимных индуктивностей между обмоткой возбуждения и каждой из фазных обмоток. Так, например, для фазы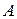

,

где - максимальное значение взаимоиндукции при совпадении магнитных осей обмоток статора и ротора.

Изменение индуктивностей фазных обмоток и взаимных индуктивностей между ними обусловлены вращением явнополюсного ротора, поскольку при этом меняется сопротивление магнитным потокам, которые определяют данные величины. Изменение магнитных потоков происходит гармонически с периодом , так как при повороте ротора на 180^о повторяется предыдущий цикл изменения магнитного сопротивления.

Так, например, индуктивность фазы 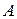определяется выражением,

,

взаимная индуктивность между обмотками фаз 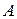и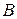

,

где , - постоянные составляющие соответствующих индуктивностей; , - амплитуды вторых гармоник соответствующих индуктивностей.

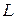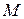Аналогично могут быть записаны выражения для и обмоток фаз В и С.

Коэффициенты в уравнениях системы (6.1) являются переменными, что значительно усложняет её решение. Дифференциальные уравнения с переменными коэффициентами называются параметрическими; аналитическое решение имеют только немногие из них. Решение системы (6.1) производится либо численными методами, либо аналитическими, предварительно преобразовав неподвижную систему координат (связанную со статором) во вращающуюся (связанную с ротором).

Чтобы учесть влияние демпферных обмоток необходимо в систему уравнений (6.1) дополнительно ввести два уравнения, соответствующие демпферных контурам в продольной и поперечной осях.

,

,

где - потокосцепление, активное сопротивление и ток демпферной обмотки по продольной оси, - потокосцепление, активное сопротивление и ток демпферной обмотки по поперечной оси.

В практических расчётах, как правило, определяется только начальное значение тока КЗ; нахождение тока КЗ в произвольный момент времени производится с помощью типовых кривых.