Определение токов при несимметричных коротких

Замыканиях

В дальнейшем будем считать, что повреждение происходит на отпайке, что позволяет исключить из рассмотрения токи нагрузки.

Фазу А будем считать особой фазой, т.е. процессы в ней будут отличаться от процессов в двух других фазах (В и С). Так однофазное КЗ будет рассматриваться в фазе А, а двухфазное КЗ и двухфазное КЗ на землю – в фазах В и С. Переходное сопротивление в месте КЗ, если это специально не оговаривается будем считать равным нулю, т.е. будем рассматривать металлическое КЗ. На основании законов Кирхгофа имеем 3 уравнения (2.4), в которых 6 неизвестных. Недостающие 3 уравнения будем брать исходя из граничных условий (соотношений для фазных токов и напряжений).

2.4.1. Двухфазное короткое замыкание. Рассмотрим двухфазное КЗ между фазами В и С (рис.2.7).

Граничные условия при двухфазном КЗ:

, , .

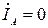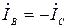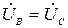Подставив граничные условия для токов в систему уравнений (2.3), получим

, ,

.

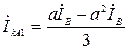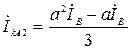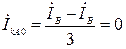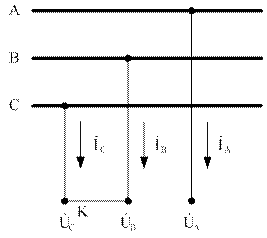
Рис.2.7. Двухфазное КЗ

Из первых двух соотношений 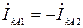. Из последнего выражения, следует, что и 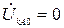, т.е. при 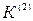нулевая последовательность отсутствует.

Подставив граничные условия для напряжений в систему уравнений (2.3), получим

,

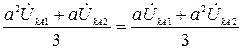следовательно, .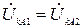

Таким образом, в месте двухфазного КЗ связь между симметричными составляющими устанавливается следующими соотношениями:

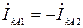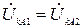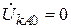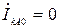, , , . (2.8)

Подставляя соотношения (2.8), в первое уравнение системы (2.4), получим

.

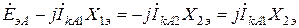Откуда ток прямой последовательности

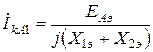. (2.9)

Ток КЗ повреждённой фазы, например, фазы В

.

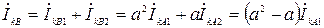Так как 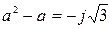, то .

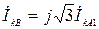Модуль тока

.

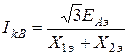Комплексная схема замещения при двухфазном КЗ, построенная в соответствие с соотношениями (2.8), изображена на рис.2.8, здесь "н"- начало, "к" – конец схемы, 1, 2, 0 – соответственно схемы замещения прямой, обратной и нулевой последовательностей. При двухфазном КЗ токи и напряжения нулевой последовательности отсутствуют, поэтому схема замещения нулевой последовательности в комплексную схему замещения не входит.

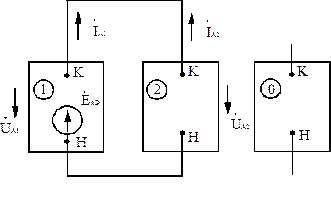
Рис.2.8. Комплексная схема замещения при двухфазном КЗ

Векторные диаграммы напряжений и токов в месте повреждения приведены на рис.2.9, а и б, соответственно. Диаграммы построены для индуктивной цепи, поэтому токи прямой последовательности отстают от соответствующих напряжений на 90 ^о

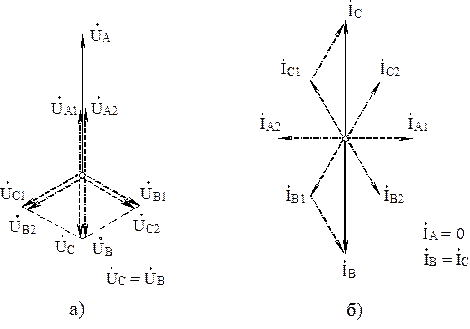
Рис.2.9. Векторные диаграммы напряжений и токов при двухфазном КЗ

Как видно из последнего рисунка здесь выполняются все граничные условия.

2.4.2. Однофазное короткое замыкание. Рассмотрим замыкание фазы А на землю (рис.2.10). Граничные условия при однофазном замыкании

, , .

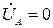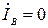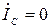Подставив граничные условия для токов в систему уравнений (2.3), получим

,

,

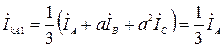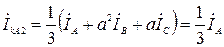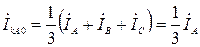
т.е.

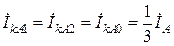. (2.10)

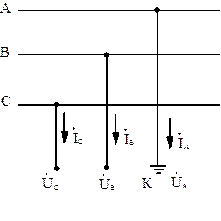
Рис.2.10. Однофазное КЗ

Из граничного условия для напряжения

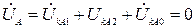. (2.11)

Подставляя в последнее выражение значения симметричных составляющих напряжений из системы (2.2), получим

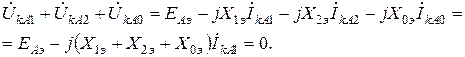
Откуда

.

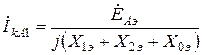Ток повреждённой фазы А .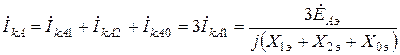

В соответствии с соотношениями (2.10) и (2.11) комплексная схема замещения при однофазном КЗ приведена на рис.2.11.

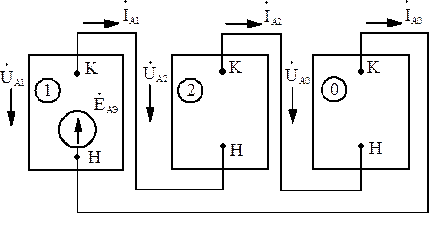
Рис.2.11. Комплексная схема замещения при однофазном КЗ

Найдём значения симметричных составляющих напряжения

; ; .

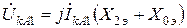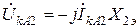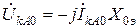Векторные диаграммы напряжений и токов в месте повреждения приведены на рис.2.12, а и б соответственно.

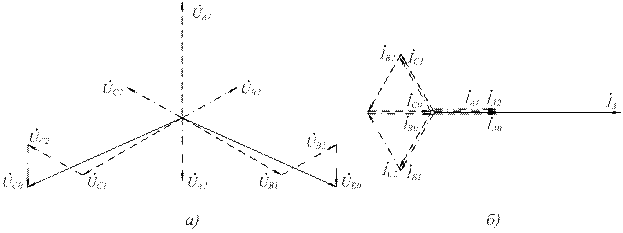
Рис.2.12. Векторные диаграммы напряжений и токов при однофазном КЗ

2.4.3. Двухфазное короткое замыкание на землю.

Рассмотрим двухфазное КЗ на землю между фазами В и С (рис.2.13).

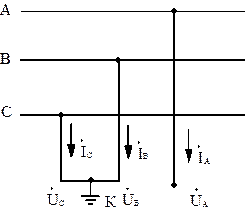
Рис.2.13. Двухфазное КЗ на землю

Граничные условия при этом:

, , .

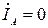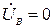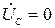Сопоставляя граничные условия при однофазном КЗ и двухфазном КЗ на землю можно установить, что граничные условия для напряжений и токов меняются местами, поэтому следует ожидать таким же образом изменятся соотношения между симметричными составляющими.

Подставив граничные условия для напряжений в систему уравнений (2.3), получим

,

,

,

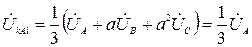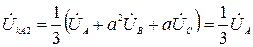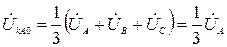т.е.

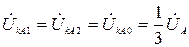(2.12)

Из граничного условия для тока

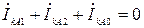. (2.13)

Подставляя в последнее выражение значения симметричных составляющих токов из системы (2.2), получим

,

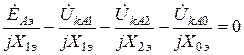или

.

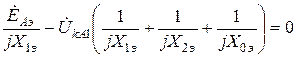Из последнего выражения

,

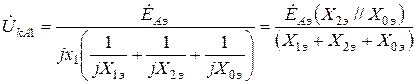откуда

,

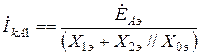где // - означает параллельное соединение (включение) элементов.

В соответствии с соотношениями (2.12) и (2.13) комплексная схема замещения при двухфазном КЗ на землю приведена на рис.2.14.

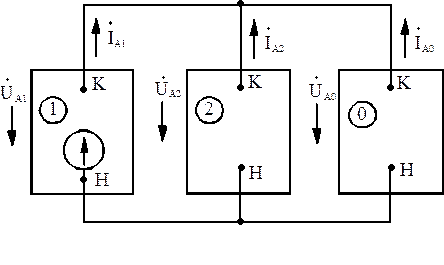
Рис. 2.14. Комплексная схема замещения при двухфазном КЗ на землю

Из комплексной схемы замещения

, ,

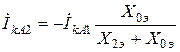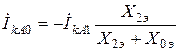Ток одной из повреждённых фаз, например, В

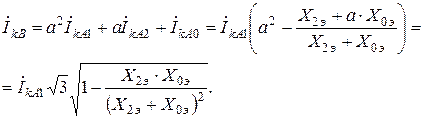
Найдём значения симметричных составляющих напряжения

;

; .

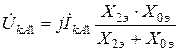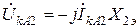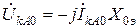Векторные диаграммы для напряжений и токов в месте повреждения приведены на рис.2.15, а и б соответственно.

Рис.2.15. Векторные диаграммы для напряжений и токов при двухфазном КЗ

На землю

ЛЕКЦИЯ 11

2.4.4. Правило эквивалентности прямой последовательности. Установленные п.п. 2.4.1-2.4.3 выражения для токов при несимметричных повреждениях показывают, что их величины пропорциональны току прямой последовательности, следовательно, абсолютную величину тока КЗ можно найти из общего выражения

,

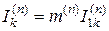где 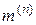- коэффициент пропорциональности, зависящий от вида КЗ, величина которого приведена в табл. 2.1, 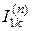- ток прямой последовательности для рассматриваемого вида КЗ.

Таблица 2.1

Вид КЗ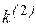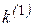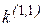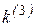

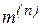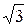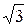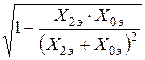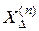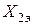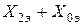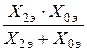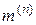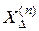Для расчёта трёхфазных КЗ метод симметричных составляющих не используется, однако значения и приведены для полноты понимания метода.

Структура полученных выражений для тока прямой последовательности в общем случае имеет вид:

,

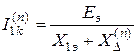где 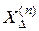дополнительное сопротивление, вводимое в схему замещения прямой последовательности, величина которого зависит от вида КЗ и не зависит от сопротивления прямой последовательности. Величина 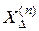определяется соотношениями, приведенными в табл.2.1.

На основании общего выражения для тока прямой последовательности было сформулировано следующее правило эквивалентности прямой последовательности: ток прямой последовательности при любом несимметричном КЗ может быть определён как ток трёхфазного КЗ в точке, удалённой от действительной точки КЗ за дополнительное сопротивление 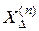, которое не зависит от параметров схемы замещения прямой последовательности (рис.2.16).

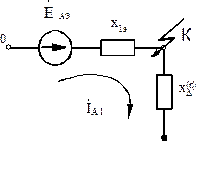
Рис.2.16. Схема для определения тока прямой последовательности при

Несимметричном КЗ

Такая трактовка тока прямой последовательности при несимметричных КЗ предполагает учёт только основной гармоники тока КЗ.

Таким образом, вычисление токов при несимметричных КЗ производится в следующей последовательности:

· составляются схемы замещения: при междуфазных замыканиях прямой и обратной последовательностей; при замыканиях на землю – прямой, обратной и нулевой последовательностей;

· схемы замещения сворачиваются и находятся эквивалентные сопротивления;

· из схемы замещения прямой последовательности также находится эквивалентная ЭДС;

· определяются 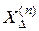и ток прямой последовательности;

· вычисляется ток КЗ.

Пример 2.2. Для схемы, приведенной на рис.2.4. произвести расчёт токов в относительных базисных единицах с приближённым приведением коэффициентов трансформации при всех видах несимметричных КЗ.

Параметры элементов схемы:

· Генератор СВ1160/180-72: 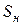=103,5 МВА; 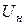=13,8 кВ; 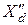=0,24;

· Трансформатор Т: ТДЦ-250000/330: 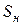=250 МВА; 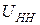=13,8 кВ; 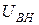=347 кВ; 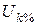=11%;

· Автотрансформатор АТДЦТН-240000/330/220 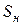= 240 МВА; 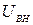=330 кВ; 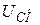= 220 кВ; 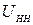= 11,0 кВ; 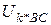= 9,5 %; 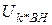=74%; 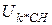= 60%;

· Линия Л1: длина l= 250 км, погонное сопротивление 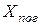= 0,32 Ом/км,

линия имеет стальные грозозащитные тросы, заземлённые на каждой опоре;

· Система: 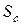= 1200 МВА.

Схемы замещения прямой, обратной и нулевой последовательностей приведены соответственно на рис.2.5, а, б и в. Выбираем базисные условия: базисную мощность 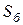= 1000 МВА и базисные напряжения ступеней, которые принимаем равными средним напряжениям: 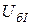=340 кВ, 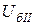=230 кВ, 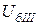=13,8 кВ, 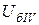=10,5 кВ. Сопротивления элементов схемы замещения прямой последовательности выражаем в относительных единицах и приводим к принятым базисным условиям:

,

,

,

,

.

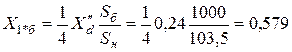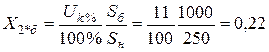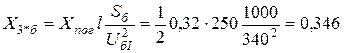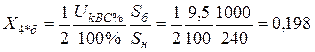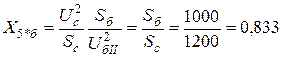Сворачивая схему замещения прямой последовательности, найдем эквивалентное сопротивление прямой последовательности

.

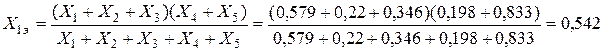При приближённом приведении ЭДС генератора и системы в относительных единицах равны 1, поэтому и эквивалентная ЭДС .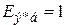

В схеме замещения обратной последовательности величина сопротивление генератора в общем случае отличается от сопротивления прямой последовательности (поэтому использован другой порядковый номер). Однако КЗ электрически удалено от генератора, поэтому будем считать сопротивление генератора обратной последовательности равным прямой. Так как все остальные элементы схем замещения прямой и обратной последовательностей одинаковы, то их эквивалентные сопротивления равны между собой .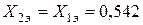

В схеме замещения нулевой последовательности сопротивления линии и системы отличаются от сопротивлений прямой (обратной) последовательностей. Для заданной линии 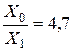, поэтому

.

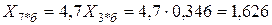В схеме замещения нулевой последовательности участвуют все обмотки автотрансформатора:

%,

%,

%,

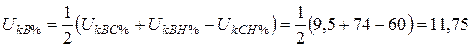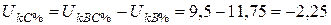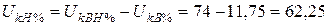соответствующие им сопротивления

,

.

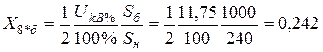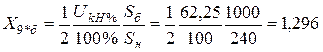Так как 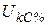представляет собой небольшую отрицательную величину, то сопротивление 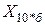принимается равным нулю.

Сворачивая схему замещения нулевой последовательности, находим эквивалентное сопротивление нулевой последовательности

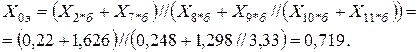
Используя приведенные выше формулы, вычисляем токи двухфазного, однофазного и двухфазного КЗ на землю в месте повреждения:

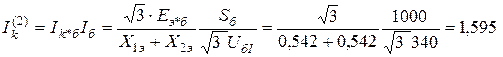кА,

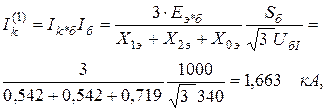
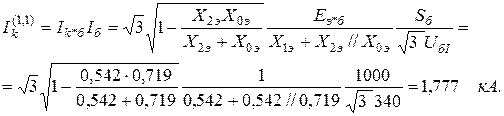
Ток трёхфазного КЗ

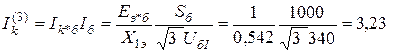кА.

2.4.5. Учёт активных сопротивлений в месте КЗ. Рассмотрим методы учёта переходных сопротивлений в месте повреждения на двух примерах.

Двухфазное КЗ при замыкании через переходное сопротивление (рис.2.17, а). Граничные условия: , , .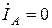

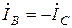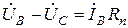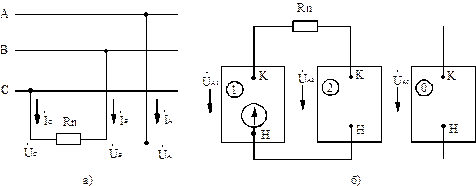
Рис.2.17. Двухфазное КЗ через переходное сопротивление (а) и комплексная схема замещения (б)

Найдем симметричные составляющие для особой фазы А, используя систему уравнений (2.3)

,

,

,

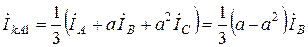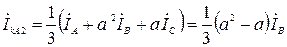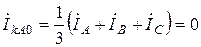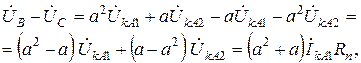
следовательно, 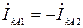и .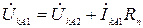

Комплексная схема замещения приведена на рис.2.17, б.

Выражение для вычисления тока КЗ при двухфазном повреждении

.

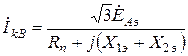Однофазное КЗ при замыкании через переходное сопротивление (рис.2.18, а).

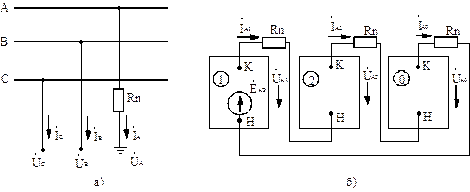
Рис.2.18. Однофазное КЗ через переходное сопротивление (а) и комплексная схема замещения (б)

Граничные условия:

, , .

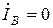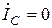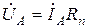Найдём симметричные составляющие для особой фазы А, используя систему уравнений (2.3)

,

,

,

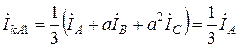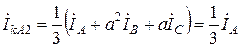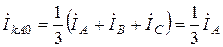т.е. ,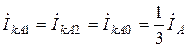

следовательно, .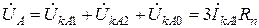

Комплексная схема замещения приведена на рис.2.18, б. Выражение для вычисления тока КЗ при однофазном повреждении

.

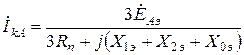ЛЕКЦИЯ 12