Подтверждение надежности систем при экспоненциальном законе наработки на отказ
В случае экспоненциального закона распределения надежность можно оценить по соотношению
h = e-λt,
где λ – интенсивность отказа; t – требуемое время работы.
Точечная оценка надежности может быть рассчитана по соотношению
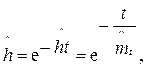
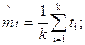 |
где
ti – продолжительность i-го испытания до отказа; k – число испытаний (полных реализаций).
Точечная оценка надежности является случайной величиной и не дает гарантированный результат. Поэтому при решении вопросов обеспечения надежности в качестве гарантированной оценки рассмотрим нижний предел доверительного интервала вероятности безотказной работы:
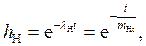
где mНt – нижняя граница доверительного интервала для математического ожидания времени безотказной работы.
Согласно определению величина mНt удовлетворяет соотношению
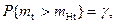 (3.13)
(3.13)
где mt – математическое ожидание времени безотказной работы,
Представим
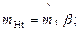
где β – корректировочный множитель, обеспечивающий выполнение соотношения (3.13); γ – принятый уровень доверительной вероятности.
После эквивалентных преобразований соотношение (3.13) можно представить в виде
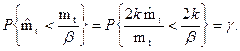
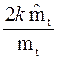 |
Как известно, случайная величина подчиняется χ2 – распределению с 2k степенями свободы, т. е.
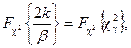
где χγ2 – квантиль χ2 – распределения по уровню γ [ 38 ].
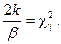 Следовательно,
Следовательно,
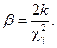 Отсюда
Отсюда
Таким образом, выражение для нижней границы mHt примет вид
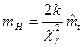 (3.14)
(3.14)
Аналогично можно получить выражение для верхней границы доверительного интервала
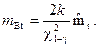
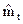 Приравнивая выражения для верхней и нижней границ заданному значению времени работы tзад и разрешая полученное соотношение относительно , получим выражения для нижней и верхней граничных кривых, определяющих области отработки элемента
Приравнивая выражения для верхней и нижней границ заданному значению времени работы tзад и разрешая полученное соотношение относительно , получим выражения для нижней и верхней граничных кривых, определяющих области отработки элемента
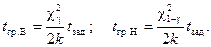 (3.15)
(3.15)
Величина tзад определяется из условия удовлетворения требований к надежности устройства
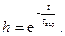
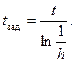 |
Отсюда
Характер изменения граничных кривых по числу испытаний для γ = 0,95 и задаваемые ими области отработ 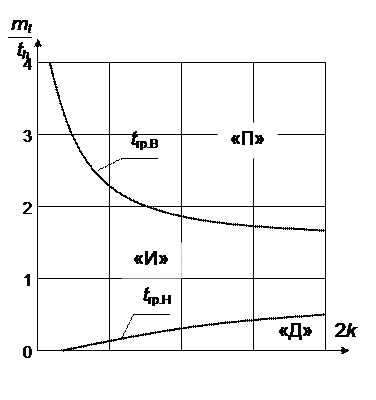 ки представлены на рис 3.2
ки представлены на рис 3.2
Рис. 3.2 Области отработки системы
Согласно графику рис. 3.2 попадание в верхнюю область “П” характеризует подтверждение надежности, так как для нее выполняется цепочка неравенств
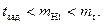
Соответственно, попадание в нижнюю область “Д” показывает невыполнение требований, предъявляемых к надежности изделия, то есть
tзад > mHt > mt.
При нахождении в средней области “И” никакого заключения сделать нельзя и испытания следует продолжить.
Рассмотренная выше модель может быть использована для прогнозирования изменения надежности в процессе проведения экспериментальной отработки. Действительно, условие подтверждения надежности можно представить в виде
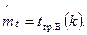
Тогда гарантией подтверждения надежности будет являться выполнение условия
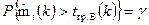
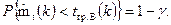 или
или
После преобразования получим
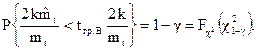
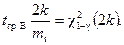 Отсюда
Отсюда
(3.16)
Подставляя (3.15) в выражение (3.16) и разрешая последнее относительно mt, получим
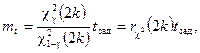
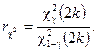
где
С учетом полученных результатов надежность устройства можно представить в виде
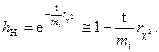 |
(3.17)
Очевидно,
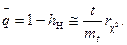
В выражении (3.17) отношение 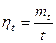 фактически характеризует коэффициент временного запаса (временной избыточности) устройства. Величина
фактически характеризует коэффициент временного запаса (временной избыточности) устройства. Величина 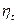 закладывается на этапе проектных разработок либо путем введения резервирования отдельных элементов, либо путем принятия соответствующих конструкторских решений.
закладывается на этапе проектных разработок либо путем введения резервирования отдельных элементов, либо путем принятия соответствующих конструкторских решений.
Зависимость подтверждаемого уровня надежности hН от числа испытаний для γ = 0,95 и различных уровней 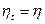 представлена на рис. 3.3.
представлена на рис. 3.3.
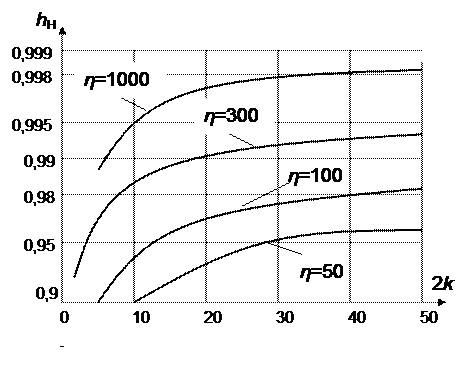 |
Рис. 3.3 Зависимость 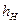 от числа испытаний k.
от числа испытаний k.
Как видно из графика, для получения приемлемых оценок надежности при ограниченных объемах испытаний, требуется обеспечить высокие уровни коэффициента временного запаса 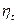 . Например, если при выполнении программы квалификационных испытаний суммарная наработка на каждый экземпляр изделия составила 35700 с то при времени работы 160 с, имеем
. Например, если при выполнении программы квалификационных испытаний суммарная наработка на каждый экземпляр изделия составила 35700 с то при времени работы 160 с, имеем
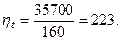
Тогда для подтверждения надежности 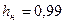 потребуется примерно 15 изделий(см. оценку
потребуется примерно 15 изделий(см. оценку 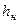 на рис. 3.3 для 2k=30).
на рис. 3.3 для 2k=30).
Лекция № 10
Планирование автономной отработки элементов систем.
При использовании оригинальных, то-есть вновь разрабатываемых элементов систем, поставленная задача сводится к обоснованию уровней параметрической избыточности, закладываемых на этапе проектной разработки отдельных элементов, а так же объемов их экспериментальной отработки. В дальнейшем рассмотрим решение этой задачи для случая нормального закона распределения параметров работоспособности устройства .
При решении поставленной задачи будем предполагать, что РН может быть представлена в виде системы с последовательно соединенными элементами. В этом случае надежность системы H равна
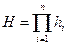 , где hi – надежность i-го элемента.
, где hi – надежность i-го элемента.
Для высоконадежных систем имеем
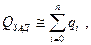 где qi =1- hi.- вероятность отказа i- го элемента.
где qi =1- hi.- вероятность отказа i- го элемента.
Соответственно точечная оценка вероятности отказа будет равна
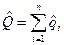 , где
, где 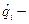 точечная оценка вероятности отказа i-го элемента.
точечная оценка вероятности отказа i-го элемента.
Для расчета верхней границы вероятности отказа системы 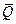 можно воспользоваться интервальной оценкой
можно воспользоваться интервальной оценкой
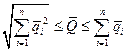 , (3.18)
, (3.18)
где  ;
; 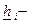 нижняя граница надежности i-го элемента системы.
нижняя граница надежности i-го элемента системы.
Нижняя граница надежности элемента 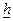 , прогнозируемая после проведении k испытаний , в случае нормального распределения параметров работоспособности, может быть оценена по соотношению
, прогнозируемая после проведении k испытаний , в случае нормального распределения параметров работоспособности, может быть оценена по соотношению
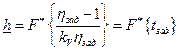 ,
,
где 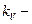 коэффициент вариации коэффициента параметрического запаса
коэффициент вариации коэффициента параметрического запаса 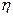 ;
;
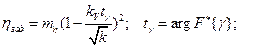
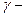 уровень доверительной вероятности;
уровень доверительной вероятности;
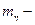 математическое ожидание коэффициента запаса; k- число испытаний;
математическое ожидание коэффициента запаса; k- число испытаний;
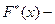 функция нормированного нормального распределения .
функция нормированного нормального распределения .
Таким образом потребный уровень математического ожидания коэффициента запаса удовлетворяет соотношению
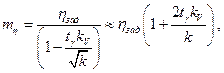
После преобразований будем иметь
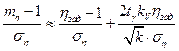 ,
,
Введя обозначения 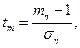
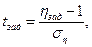
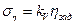 ,
,
получим 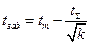 .
.
Таким образом 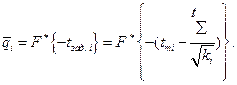 , где
, где 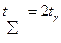 .
.
Следовательно, требуемый уровень надежности может быть подтвержден при различных комбинациях параметров tmi и 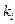 . Среди многообразия этих значений целесообразно выбрать те, которые обеспечивают заданный уровень вероятности отказа при минимальных затратах средств.
. Среди многообразия этих значений целесообразно выбрать те, которые обеспечивают заданный уровень вероятности отказа при минимальных затратах средств.
Очевидно, уровень избыточности элементов системы tmi будет определять производственные и эксплуатационные расходы на выполнение программы:
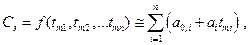
где 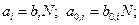 N – объем выпускаемой продукции;
N – объем выпускаемой продукции;
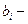 коэффициент чувствительности, характеризующий удельные затраты
коэффициент чувствительности, характеризующий удельные затраты
на обеспечение единицы надежности, выраженной в гауссах.
Параметр 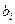 определяется уровнем избыточности элемента. В частности, при использовании «горячего» резерва вероятность отказа резервной группы
определяется уровнем избыточности элемента. В частности, при использовании «горячего» резерва вероятность отказа резервной группы 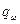 оценивается по соотношению
оценивается по соотношению
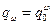 ,
,
где 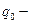 вероятность отказа нерезервированного элемента;
вероятность отказа нерезервированного элемента; 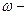 условная кратность резерва.
условная кратность резерва.
Отсюда 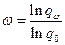 .
.
Очевидно стоимость резервированного элемента будет равна
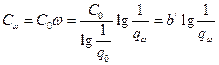 ,
,
где 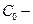 стоимость нерезервированного элемента;
стоимость нерезервированного элемента;
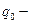 вероятность отказа нерезервированного элемента;
вероятность отказа нерезервированного элемента;
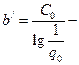 затраты на единицу надежности, выраженной в беллах.
затраты на единицу надежности, выраженной в беллах.
Переходя к оценке надежности в гауссах, получим
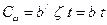 , где
, где 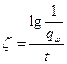 ;
; 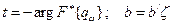 .
.
Очевидно параметр b характеризует удельные затраты на единицу надежности, выраженной в гауссах.
Зависимость стоимости от кратности резерва можно представить в виде
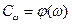
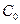 .
.
Вид функции 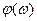 зависит от типа резервирования .Очевидно, в случае «горячего» резерва , имеем
зависит от типа резервирования .Очевидно, в случае «горячего» резерва , имеем 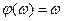 .
.
. Для «холодного» резерва стоимость резервной группы представим в виде
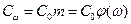 ,
,
где m – общее число элементов в резервной группе.
Отсюда 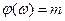 .
.
Для нахождения m воспользуемся приближенной оценкой 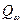
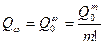 .
.
.
После логарифмирования, получим
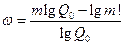 .
.
При решении задачи дискретную функцию 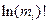 аппроксимируем непрерывной зависимостью. В дальнейшем проанализируем характер изменения
аппроксимируем непрерывной зависимостью. В дальнейшем проанализируем характер изменения  по
по 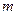 для
для 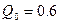 . .Расчеты проводились по программе Mathcad. При написании программы были приняты следующие обозначения:
. .Расчеты проводились по программе Mathcad. При написании программы были приняты следующие обозначения: 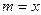 ,
, 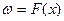 . Функция F(x) рассчитывалась по соотношению
. Функция F(x) рассчитывалась по соотношению

При проведении практических расчетов зависимость F(x), в окрестности оптимального решения, можно аппроксимировать прямой
. 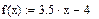
Таким образом, для рассматриваемого случая, можно принять
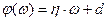 , где
, где  .
.
Функции F(x) и f(x) представлены на рис. 3.4.
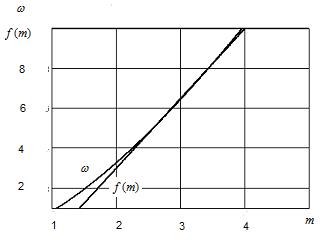
Рис. 3.4. Зависимость кратности резерва  и аппроксимирующей прямой
и аппроксимирующей прямой 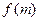
от общего числа элементов в резервной группе 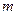 .
.
В дальнейшем найдем аналогичные соотношения для элементов с параметрической избыточностью. При решении поставленной задачи, вероятность отказа элементов с параметрической избыточностью условно представим в виде
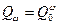
где 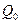 - вероятность отказа элемента, соответствующая коэффициенту запаса
- вероятность отказа элемента, соответствующая коэффициенту запаса 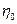 ;
; 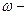 условная кратность резерва.
условная кратность резерва.
Согласно результатам, полученным в работе [ 7 ], надежность элемента 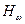 ,прогнозируемая после проведении k испытаний , может быть оценена по соотношению
,прогнозируемая после проведении k испытаний , может быть оценена по соотношению
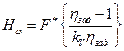 ,
,
где 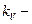 коэффициент вариации коэффициента запаса;
коэффициент вариации коэффициента запаса;
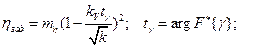
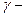 уровень доверительной вероятности;
уровень доверительной вероятности;
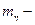 математическое ожидание коэффициента запаса.
математическое ожидание коэффициента запаса.
Знание 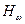 , позволяет оценить условную кратность резерва
, позволяет оценить условную кратность резерва
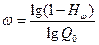 ,
,
В дальнейшем будем считать, что стоимость резервированного элемента пропорциональна коэффициенту запаса 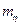 . Тогда функцию
. Тогда функцию 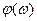 можно оценить по соотношению
можно оценить по соотношению 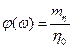 .
.
Характер изменения функции 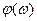 представлен на рис. 3.5
представлен на рис. 3.5
.
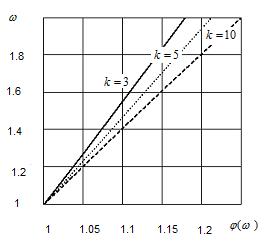
Рис.3.5 Характер зависимости кратности резерва  для различных
для различных 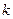 от функции
от функции
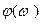 для элементов с параметрической избыточностью.
для элементов с параметрической избыточностью.
При построении графика были приняты следующие исходные данные:
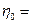 1.3 ;
1.3 ; 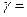 0,95 ;
0,95 ; 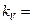 0,1 ;
0,1 ; 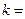 3, 5, 10.
3, 5, 10.
Как видно из графика функция 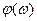 слабо зависит от объема испытаний k . Приближенно для функции
слабо зависит от объема испытаний k . Приближенно для функции 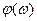 =
= 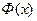 может быть принята линейная аппроксимационная зависимость
может быть принята линейная аппроксимационная зависимость
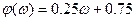 (
( 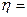 0.25).
0.25).
.
С учетом полученных результатов, выражение для стоимости примет вид
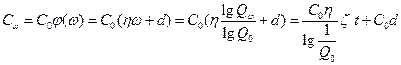 ,
,
где 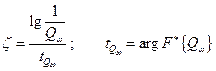
Отсюда
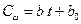 , где
, где 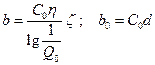 .
.
Для рассмотренного в примере случая : 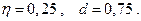
Соответственно затраты на экспериментальную отработку будут определяться объёмами испытаний элементов
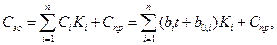
где Ci - затраты на проведение одного испытания i-го элемента,
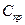 – затраты, не зависящие от варьирующихся параметров.
– затраты, не зависящие от варьирующихся параметров.
Таким образом, решение задачи сводится к минимизации функции суммарных затрат
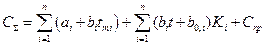 (3.19)
(3.19)
В качестве дисциплинирующего условия рассмотрим правую границу неравенства (3.18)
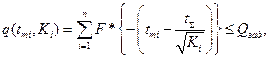
В дальнейшем для нахождения оптимального решения задачи рассмотрим функцию Лагранжа
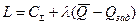
Оптимальные параметры будут удовлетворять системе алгебраических уравнений:
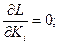
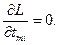
При нахождении производной 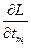 , предполагая, что число испытаний
, предполагая, что число испытаний 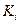 существенно меньше объема транспортной программы N, вторым слагаемым в выражении (2.36) можно пренебречь. Поэтому в дальнейшем удельные затраты на проведение одного испытания
существенно меньше объема транспортной программы N, вторым слагаемым в выражении (2.36) можно пренебречь. Поэтому в дальнейшем удельные затраты на проведение одного испытания 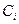 будем считать постоянными для каждого i-го элемента системы.
будем считать постоянными для каждого i-го элемента системы.
Производя дифференцирование, получим:
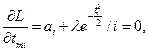
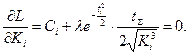 (3.20)
(3.20)
Разрешая систему уравнений относительно Ki, найдем
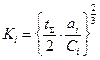 (3.21)
(3.21)
Соотношение (3.21) позволяет оценить оптимальный объем испытаний с точностью до целых. Таким образом оптимальные объемы испытаний отдельных элементов не зависят от требований, предъявляемых к надежности систем и определяются соотношением удельных затрат на обеспечение единицы надежности, закладываемой на этапе проектирования, 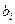 и затрат на проведение одного испытания
и затрат на проведение одного испытания 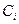 .
.
Соответственно, из первого уравнения системы (3.20) получим:
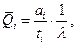
где 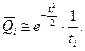
Подставляя 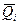 в граничное условие , приходим к соотношению:
в граничное условие , приходим к соотношению: 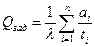 . Отсюда
. Отсюда 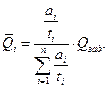 (3.22)
(3.22)
Таким образом, оптимальные уровни вероятности отказа пропорциональны удельным затратам 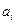 и заданным требованиям к вероятности отказа системы
и заданным требованиям к вероятности отказа системы 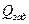 .
.
Заметим, что предположение о постоянстве 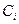 , принятое выше, может не выполняться при создании единичных КА, затраты на разработку и экспериментальную отработку которых, существенно превышают затраты на изготовление и применение этих комплексов. Они могут составлять до 70% от общих затрат на всю программу. В этом случае решение должно быть уточнено.
, принятое выше, может не выполняться при создании единичных КА, затраты на разработку и экспериментальную отработку которых, существенно превышают затраты на изготовление и применение этих комплексов. Они могут составлять до 70% от общих затрат на всю программу. В этом случае решение должно быть уточнено.
Лекция №11
В случае экспоненциального распределения наработки на отказ нижняя граница надежности элемента равна
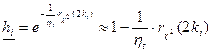 ,
,
где 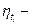 коэффициент временного запаса.
коэффициент временного запаса.
Характер изменения функции 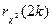 представлен на рис. 3.6 При построении графика были приняты следующие обозначения:
представлен на рис. 3.6 При построении графика были приняты следующие обозначения: 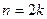 ,
, 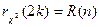 ,
, 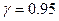 .
.
Расчеты проводились по соотношению [8]:
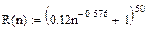 (3.23)
(3.23)
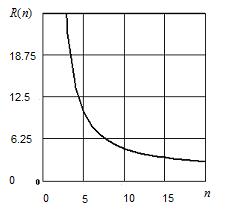
Рис. 3.6 Зависимость функции 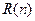 от параметра
от параметра 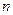 .
.
Очевидно, что 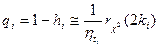
В общем случае надежность технической системы будет определяться уровнями надежности отдельных элементов, входящих в ее состав и типом их соединения. При последовательно соединении элементов вероятность отказа технической системы приближенно можно оценить по соотношению
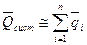 где
где 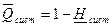 .
.
Отсюда получим
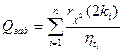 (3.24)
(3.24)
где 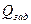 - заданная вероятность отказа системы.
- заданная вероятность отказа системы.
Следовательно, требуемый уровень надежности системы может подтвержден при различных комбинациях параметров 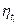 и
и 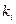 . Среди многообразия значений
. Среди многообразия значений 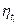 и
и 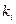 целесообразно выбрать те, которые обеспечивают заданный уровень надежности при минимальных затратах.
целесообразно выбрать те, которые обеспечивают заданный уровень надежности при минимальных затратах.
Очевидно, уровни избыточности элементов системы mti будут определять эксплуатационные расходы на выполнение программы
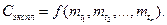 (3.25)
(3.25)
