Расчет надежности систем с последовательным соединением элементов.

Классификация систем

Рассмотренные выше теории надежности позволяют решать задачи оценки надежности различных технических устройств. В общем случае любое изделие состоит из целого ряда отдельных систем, отличающихся по функциональному признаку, то есть по тем задачам, которые они решают. В частности, в составе ЛА можно рассматривать cледующие системы: полезная нагрузка, конструкция, система управления (СУ), двигательная установка (ДУ), система разделения и сброса, энергосистема, бортовая кабельная сеть (БКС) и т.д. следовательно, оценка надежности всего изделия требует проведения расчетов надежности для отдельных систем, входящих в его состав. Анализ работоспособности различных систем показывает, что несмотря на широкое разнообразие различных типов систем, все они с точки зрения оценки их надежности могут быть подразделены на два основных класса:

1) системы с последовательным соединением элементов;

2) системы с параллельным соединением элементов;

3) системы произвольной структуры.

Система относится к классу систем с последовательным соединением элементов, если отказ системы происходит при отказе хотя бы одного из элементов, входящих в его состав. Графически такие системы изображают в виде последовательной цепочки элементов (рис. 2.1). Отказ какого-либо из элементов приводит как бы к обрыву цепочки и, следовательно, отказу всей системы.

Рис. 2.1 Схема системы с последовательным соединением элементов

Согласно приведенному определению летательный аппарат в целом можно представить как систему, из последовательно соединенных подистем, входящих в его состав (ДУ; СУ; конструкция и т.д.), так как отказ любой из под систем приводит к отказу всего ЛА.

В качестве систем с последовательным соединением можно также рассмотреть конструкцию топливных баков ЛА. Упрощенно можно выделить в составе одного из баков три элемента: верхнее днище, обечайка, нижнее днище. Очевидно отказ любого из элементов (то есть их разрушение) приведет к нарушению герметичности отсека и, следовательно, к его отказу.

Система относится к классу систем с параллельным соединением элементов, если отказ системы происходит только при отказе всех элементов, входящих в ее состав.

Условно такие системы изображаются в виде параллельной цепочки элементов (рис.2. 2). Следовательно, при отказе одного элемента его задачу выполняют оставшиеся, и система откажет только при отказе всех элементов в составе системы. Очевидно, к рассмотренному классу относятся резервные системы.

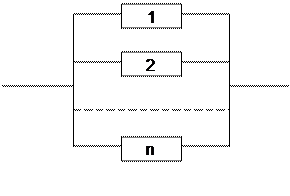
Рис..2.2 Схема параллельного соединения элементов.

В качестве примера резервных систем можно рассмотреть систему ЛА, предназначенную для поражения цели, систему КЛА, предназначенною для решения одной и той же задачи (например, запуск двух аппаратов «Венера»), резервирование отдельных блоков системы управления ЛА и т.д.

Системы с последовательным соединением элементов

Согласно определению, надежность системы с последовательным соединением элементов характеризуется вероятностью выполнения условий работоспособности для всех элементов системы, то есть

Н = P{ρ₁(t) > 0,… ρ_n(t) > 0; 0 < t < T} (2.1)

где ρ_i(t) – функция работоспособности i-го элемента;

Т – время функционирования системы.

В дальнейшем будем предполагать, что функции работоспособности является случайными величинами. Тогда надежность системы может быть выражена через дифференциальный закон распределения системы n случайных величин

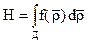(2.2)

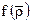где - многомерный дифференциальный закон распределения систем случайных величин ρ₁, ρ₂,…, ρ_n,

Д – область интегрирования, определяется системой неравенств ρ_i > 0, i = 1,2,…,n.

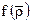Проведение расчетов по соотношению (2.2) требует знания многомерного закона распределения и вычисление многомерного интеграла, которой обычно требует использования численных методов с привлечением ЭВМ. Поэтому для практических расчетов оказывается полезным значение приближенных оценок надежности. Рас­смотрим вывод этих оценок на примере простейшей системы из двух элементов. Согласно (1) надежность такой системы равна

H = P{ρ₁ > 0; ρ₂ > 0} (2.3)

Тогда по теореме умножения вероятности, получим

H = P{ρ₁ > 0}P{ρ₂ > 0 / ρ₁ > 0} (2.4)

Для случая независимых элементов выражение (2.4) упростится

H = P{ρ₁ > 0}P{ρ₂ > 0} = h₁ h_{2 (2.5)}

где h_i = P{ρ_i > 0} – надежность i-го элемента системы.

Если элементы зависимы для оценки надежности системы необходимо вычислить условную вероятность

P{ρ₂ > 0 / ρ₁ > 0}

Рассмотрим определение этой вероятности для случая линейно зависимых элементов (см. рис.2.3)

ρ₂ = 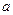ρ₁ + b ; , .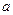

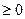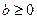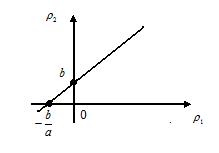
Рис.2.3 Линейная зависимость параметров

Как видно из графика, при ρ₁ > 0 значения ρ₂ будут всегда положительны. Таким образом, условная вероятность P{ρ₂ > 0 / ρ₁ > 0} будет равна единице, как вероятность достоверного события. Отсюда

H = P{ρ₁ > 0} = h₁ (2.6)

Для зависимости, представленной на рис.2.3, в случае отказа пер­вого элемента (ρ₁ < 0) второй элемент на участке изменения α < ρ₁ < 0 еще не утрачивает свою работоспособность, то есть ρ₂ > 0. Следовательно, второй элемент имеет более высокую надежность. По­этому соотношение (2.4) можно представить так

H = min {h₁,h₂}

Знание уровней надежности система для двух рассмотренных случаев позволяет записать следующую оценку

h₁,h₂ ≤ H ≤ min {h₁,h₂}

Аналогичные соотношения можно получить для системы с произ­вольным числом элементов n

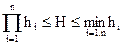(2.7)

где h_i – надежность i-го элемента системы.Равенство справа выполняется в случае линейной зависимости элементов (r = 1), Нижняя оценка является точной для системы с независимыми элементами (r = 0).

При промежуточных значениях коэффициента корреляции r надежность лежит внутри диапазона (2.7). Проследим характер измене­ния Н в зависимости от коэффициента корреляции на простейшем при­мере.

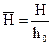Рассмотрим систему, состоящую из двух равнонадежных элемен­тов h₁ = h₂ = h₀, функции, работоспособности которых подчине­ны нормальному закону распределения. График изменения относительной надежности такой системы в зависимости от r для различных значений h₀ представлен на рис.2.4.

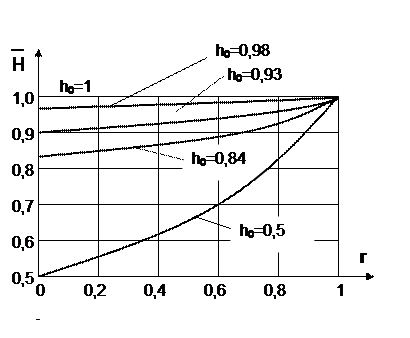
Рис.2.4 График изменения относительной надежности

системы зависимости от r для различных значений h₀

Как видно из графика с увеличением r надежность системы растет и при r = 1 достигает максимального значения, равного надежности одного элемента.

Для независимых элементов (r = 0) с увеличением числа элементов надежность будет падать. Характер зависимости надежности системы от числа элементов N Поэтому при проработке проектно-конструкторских решений (ПКР) стремятся либо к наиболее простым решениям, обеспечивающих минимальное число элементов, либо к решениям, обеспечивающим условия линейной зависимости элементов.

В частности для обеспечения высокой надежности раскрытия стыка Н_ст = hⁿ_РБ, где h – надежность срабатывания одного пироболта; n – число пироболтов используют ограниченное число пироболтов, хотя это и приводит к улучшению нагружения отсека и его массовых характеристик. Этот подход используется для обеспечения надежности поперечных стыков РН. Для продольных стыков, характерных для конструкции сбрасываемых обтекателей, переходят на механические замки, конструкция которых обеспечивает линейную зависимость элементов в смысле надежности.

Для иллюстрации проанализируем систему сброса головного обтекателя, предоставленного на рис. 2.5а; 2.5б. Эта схема отделения (см. рис. 2.5а) характеризуется наличием поперечного и продольного стыков. Разрыв силовых связей продольного и поперечного стыков осуществляется в заданный момент по команде от системы управления. Обтекатель, разделенный на две створки, начинает вращаться вокруг оси разворота под действием средств увода. После достижения заданного угла поворота створок происходит разрыв силовой связи в узлах разворота, и створки уводятся от корпуса РН с помощью толкателей.

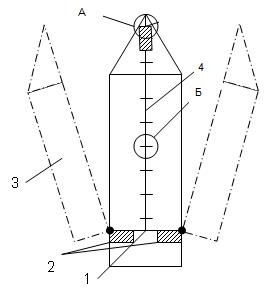
Рис. 2.5 а. Схема двухстворчатого обтекателя с пружинными толкателями:

1 – стыковочный шпангоут; 2 – толкатели сброса створок; 3 – створки обтекателя;

4 – продольный стык

II

I

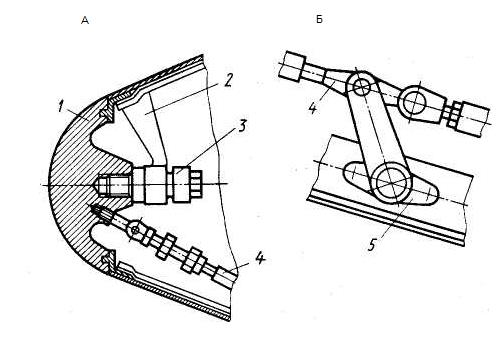
Рис.2.5 б. Элементы системы раскрытия продольного стыка

На одной из створок обтекателя с помощью кронштейна 2 (см.рис. 2.5 б ) устанавливается привод 3 (пневматический, пружинный, пороховой). В результате срабатывания привода происходит перемещение вперед (относительно створок) наконечника 1 и поворот относительно своих осей кронштейнов замков 5. Замки соединены между собой и с наконечником тягами 4. Очевидно, для успешного раскрытия замков необходимо, чтобы усилие привода превысило силы сопротивления фиксатора и усилия срабатывания элементов продольного стыка. Раскрытие продольного стыка происходит при освобождении защелок всех механических замков стыка, когда ход толкателя продольного стыка l_т = l₁. Таким образом, вероятность раскрытия

h_p = P(l_т ≥ l₁) или h_p = P(N_д > N_п),

где N_д – минимальное усилие пружины толкателя; N_п – сила сопротивления движению.

Предполагая, что законы распределения N_д и N_п нормальные, а сами нагрузки независимые, получим

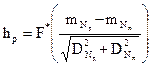Полученная оценка характеризует как раскрытие одного замка продольного стыка так и раскрытия стыка в целом.

Лекция №4