Расчет надежности элемента системы.
Надежность элемента по формальной теории оценивается по соотношению (1.7).
Если известны интенсивности отказа λ нахождение основных показателей надежности не представляет особого труда. Интенсивности отказов λ определяются статистически.
Значения интенсивности отказов некоторых комплектующих элементов при номинальных условиях их функционирования представлены в табл. 2.1 [15].
Значения интенсивностей отказа Таблица 2.1
| Изделия | Число отказов за 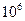 часов часов |
| Гидроцилиндры | 0,03 |
| Шариковые подшипники | 0,011 |
| Осевые вентиляторы | 0,125 |
| Дизельные двигатели | 0,898 |
| Механические фильтры | 0,035 |
| Гидравлическая арматура | 2,77 |
| Уплотнения | 0,011 |
| Электронагревательные устройства | 0,355 |
| Гибкие шланги | 1,74 |
| Механические силовые редукторы | 0,146 |
| Муфты | 0,441 |
| Электродвигатели постоянного тока | 0,22 |
| Электродвигатели переменного тока | 0,499 |
| Генераторы переменного тока | 0,796 |
| Топливные насосы | 0,114 |
| Гидравлические насосы | 0,043 |
| Электромагнитные клапаны | 0,194 |
| Топливные клапаны | 0,127 |
| Гидравлические клапаны | 0,99 |
| Пневматические клапаны | 0,214 |
| Силовые трансформаторы | 0,0012 |
| Аккумуляторные свнцово-кислотные батареи | 0,006 |
| Конденсаторы переменные | 0,025 |
| Конденсаторы плёночные постоянной ёмкости | 0,45 |
| Магнитные сердечники ЭВМ | 0,00002 |
| Диск памяти | 0,148 |
| Выпрямители кремниевые регулируемые | 0,017 |
| Реле общего назначения | 0,032 |
| Тепловые реле | 2,00 |
| Сопротивления переменные общего назначения | 0,02 |
| Проволочные переменные сопротивления | 0,163 |
| Электромагниты | 0,3 |
| Переключатели общего назначения | 0,021 |
Отличия условий функционирования и уровня нагружения от номинальных учитываются в расчетах надежности зависимостями интенсивности отказа от рабочей температуры и характера нагружения анализируемых комплектующих элементов. В частности
зависимость интенсивности отказа конденсаторов от внешних условий и режимов работы можно представить в виде [3]
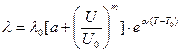 ,
,
где 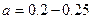 ;
; 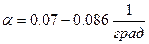 ; m=3.5-5 для бумажных конденсаторов,
; m=3.5-5 для бумажных конденсаторов,
4.0-5.0-для слюдяных и 3.0-для керамических; 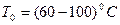 .
.
При проведении расчетов надежности элементов по общей теории условие работоспособности по каждому из параметров представим в виде неравенства
η > 1 ,
где η = хдоп / хд – коэффициент запаса по рассматриваемому параметру;
хд , хдоп – соответственно действующее и допустимое значение параметра.
Тогда вероятность отказа по данному параметру можно представить в виде
Q = Р{η < 1}
В предположении нормального закона распределения коэффициента запаса η , получим
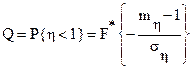
где mη – математическое ожидание коэффициента запаса;
ση – среднеквадратическое отклонение коэффициента запаса.
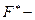 функция нормированного нормального распределения ( см. табл. 2.2 )
функция нормированного нормального распределения ( см. табл. 2.2 )
Функция нормированного нормального распределения 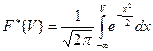
Таблица 2.2
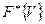 | V | 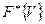 | V | 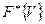 | V |
| 0,5 | 0,68 | 0,468 | 0,86 | 1,08 | |
| 0,51 | 0,025 | 0,69 | 0,496 | 0,87 | 1,126 |
| 0,52 | 0,051 | 0,7 | 0,524 | 0,88 | 1,175 |
| 0,53 | 0,075 | 0,71 | 0,553 | 0,89 | 1,227 |
| 0,54 | 0,1 | 0,72 | 0,583 | 0,9 | 1,281 |
| 0,55 | 0,125 | 0,73 | 0,613 | 0,91 | 1,341 |
| 0,56 | 0,150 | 0,74 | 0,643 | 0,92 | 1,405 |
| 0,57 | 0,176 | 0,75 | 0,674 | 0,93 | 1,476 |
| 0,58 | 0,202 | 0,76 | 0,706 | 0,94 | 1,555 |
| 0,59 | 0,228 | 0,77 | 0,739 | 0,95 | 1,645 |
| 0,6 | 0,254 | 0,78 | 0,772 | 0,96 | 1,751 |
| 0,61 | 0,279 | 0,79 | 0,806 | 0,97 | 1,881 |
| 0,62 | 0,306 | 0,8 | 0,842 | 0,98 | 2,054 |
| 0,63 | 0,332 | 0,81 | 0,878 | 0,99 | 2,326 |
| 0,64 | 0,358 | 0,82 | 0,915 | 0,999 | 3,09 |
| 0,65 | 0,385 | 0,83 | 0,954 | 0,9999 | 3,72 |
| 0,66 | 0,412 | 0,84 | 0,995 | 0,99999 | 4,265 |
| 0,67 | 0,440 | 0,85 | 1,036 |
Для оценки mη и ση воспользуемся методом линеаризации. Разлагая функцию η в ряд Тейлора в окрестности математического ожидания аргументов и ограничиваясь линейными членами, получим
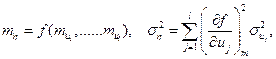
где 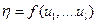 ;
; 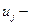 независимые случайные величины, определяющие случайный характер функции работоспособности.
независимые случайные величины, определяющие случайный характер функции работоспособности.
В общем случае выражение для дисперсии примет вид
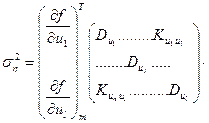
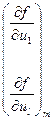 ,
,
где 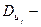
 дисперсия j-ого аргумента;
дисперсия j-ого аргумента; 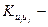 корреляционный момент i-го и j-го аргументов.
корреляционный момент i-го и j-го аргументов.
Для отношения двух независимых случайных величин получим
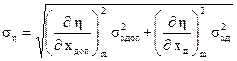
mη = mхдог / mхд,
где mхд , mхдог – соответственно математические ожидания действующих и допустимых значений параметров;
σхд, σхдоп – соответственно средние квадратические отклонения действующих и допустимых значений параметров.
Индекс «m» в выражении для ση означает, что частные производные берутся в точке математического ожидания аргументов.
После преобразований выражение для ση представим в виде
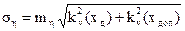
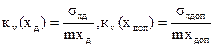
где - соответственно коэффициенты вариации
действующих и допустимых значений параметров.
Подставляя выражение для ση в соотношение для Q, получим
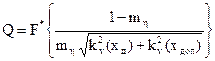
Таким образом, для оценки вероятности отказа по каждому параметру необходимо знание коэффициентов вариации действующих и допустимых значений параметров и коэффициента запаса η При проведении анализа будем считать известными значения коэффициентов вариации по каждому из рассматриваемых параметров. Введение этого допущения не снижает практической ценности исследования. Действительно, коэффициенты вариации обладают свойством стабильности и поэтому их значения могут быть рассчитаны по статистическим данным, полученным ранее для аналогичных изделий.
В дальнейшем рассмотрим задачу оценки 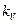 для функций различного вида. Сначала рассмотрим аддитивную функцию двух переменных. Пусть
для функций различного вида. Сначала рассмотрим аддитивную функцию двух переменных. Пусть
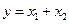 ,
,
где 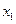 и
и 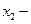 независимые, положительно определенные случайные величины.
независимые, положительно определенные случайные величины.
Для данного случая имеем
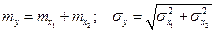
Выражения удобней представить в виде
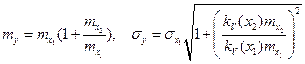 .
.
Далее предполагая, что отношение 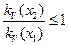 , можно получить следующую оценку
, можно получить следующую оценку
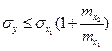
Отсюда 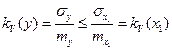
Аналогично в предположении, что 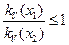 , получим
, получим 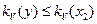 .
.
Таким образом в общем случае можно записать 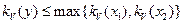 .
.
Эта оценка может быть уточнена, если известен вклад каждого из слагаемых в суммарную функцию 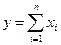 . Предполагая независимость
. Предполагая независимость 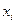 , получим
, получим
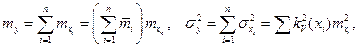
где 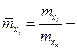 относительный вклад i-го слагаемого;
относительный вклад i-го слагаемого;
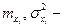 математическое ожидание и дисперсия i-го параметра ;
математическое ожидание и дисперсия i-го параметра ;
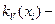 коэффициент вариации i-го параметра.
коэффициент вариации i-го параметра.
Тогда
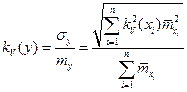 .
.
В дальнейшем рассмотрим функцию равную произведению двух переменных : 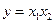 .
.
.Производя линеаризацию функции y в окрестности математических ожиданий случайных величин 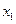 и
и 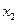 получим
получим
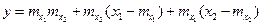 .
.
Тогда выражения для 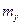 и
и 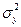 примут вид
примут вид
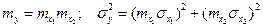 .
.
Отсюда найдем 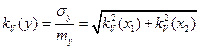 .
.
Аналогично можно показать, что оценка остается справедливой и для случая, когда y является отношением двух независимых случайных величин 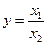 .
.
Нетрудно заметить, что полученные выше формулы путем последовательной группировки слагаемых ( или сомножителей ) легко обобщить на случай трех и более переменных. Так для функции 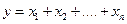 формула для
формула для 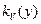 примет вид
примет вид
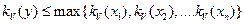
Аналогично для функции 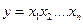 имеем
имеем
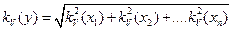
Более того методом последовательной группировки можно находить искомые оценки коэффициента вариации для различных комбинаций исходных параметров. Так для функции вида 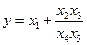 получим
получим
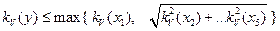
В заключение найдем оценку коэффициента вариации для функции одной переменной
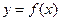 . Используя метод линеаризации и производя выкладки, аналогичные предыдущим, получим
. Используя метод линеаризации и производя выкладки, аналогичные предыдущим, получим
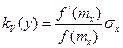
В частности для функции 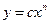 получим
получим 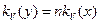 .
.
Для иллюстрации полученных результатов в дальнейшем оценим надежность элемента конструкции.
При расчете гладких цилиндрических оболочек обычно рассматриваются следующие действующие напряжения:
1. Меридиональные 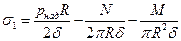 ,
,
2. Кольцевые 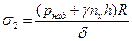 ,
,
где 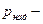 внутреннее избыточное давление; R—радиус оболочки;
внутреннее избыточное давление; R—радиус оболочки; 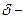 толщина оболочки;
толщина оболочки;
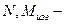 осевая сжимающая сила и изгибающий момент;
осевая сжимающая сила и изгибающий момент; 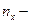 осевая перегрузка;
осевая перегрузка;
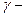 плотность компонента топлива;
плотность компонента топлива; 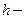 высота столба жидкости в баке.
высота столба жидкости в баке.
В дальнейшем, для примера, рассмотрим надежность конструкции оболочки бака, работающего на внутреннее избыточное давление. В этом случае коэффициент запаса будет равен 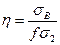 , где
, где 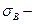 предел прочности материала бака на растяжение;
предел прочности материала бака на растяжение;
При проведении расчета примем следующие исходные данные:
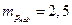 атм.;
атм.;  1,5;
1,5; 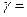 1,14 т/м; R=2 м; h=3м ;
1,14 т/м; R=2 м; h=3м ; 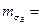 320 МПа ;
320 МПа ; 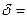 3мм;
3мм;
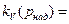 5% ;
5% ; 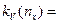 5% ;
5% ; 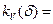 2% ;
2% ; 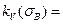 3%.
3%.
Результаты расчета 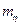 представлены ниже:
представлены ниже:
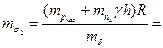
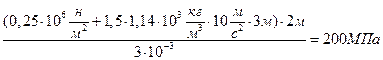 ;
;
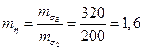 ;
;
Соответственно для коэффициентов вариации получим
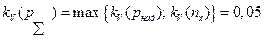 ;
;
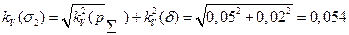 ;
;
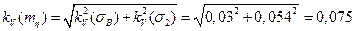 .
.
Таким образом вероятность неразрушения оболочки будет равна
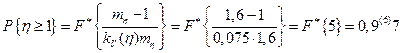 .
.
При расчете на устойчивость критические нагрузки оцениваются по соотношению
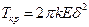 .
.
Действующие усилия удобней представить в виде
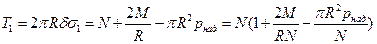 .
.
Соответственно математическое ожидание 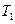 будет равно
будет равно
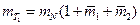 , где
, где 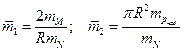 .
.
Лекция №3
