Формальная теория надежности

Для прогнозирования уровня проектной надежности изделий в зависимости от их вида и условий функционирования могут быть использованы два принципиально различных подхода, обоснование которых дается соответственно формальной теорией надежности и общей теорией.

В формальной теории принято, что изменение надежности во времени подчинено некоторым статистическим зависимостям, которые определяются лишь из эксперимента. Физическая сущность причины отказа в этом случае не выясняется.

Формальная теория надежности обычно используется при расчете надежности радиоэлектронной аппаратуры, электромеханических агрегатов и механизмов, работоспособность которых определяется по снашиваемости. В этом направлении работали такие видные ученые как Борг, Гнеденко, Сотсков и другие.

Основные количественные характеристики надежности в этом случае связаны со временем работы изделия и определения из большого числа экспериментов. К ним относятся:

1. Среднее время функционирования изделия - Т;

2. Интенсивность отказа –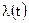

3. Вероятность безотказного функционирования изделия в течение заданного промежутка времени – Р(t)

Поясним более подробно смысл второй характеристики – 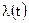. Согласно определению, под интенсивностью отказа понимается вероятность того, что изделие, проработавшее до момента времени t , откажет в следующую единицу времени.

Применение тех или иных показателей зависит от конкретной постановки задачи. Так при оценки эффективности поражения цели нас интересует вероятность выполнения задачи, а следовательно, в качестве показателя надежности надо рассматривать вероятность безотказного функционирования изделия.

В то же время при оценке эффективности функционирования орбитального комплекса нас может интересовать среднее время его безотказного функционирования - Т, то есть первая характеристика. Между тремя рассмотренными характеристиками существует взаимнооднозначное соответствие, то есть они могут быть выражены друг через друга. Для нахождения этого соответствия проанализируем возможное состояние изделия в процессе функционирования. Очевидно, их всего два: 1 – работоспособное , 2 – состояние отказа. Причем, в процессе функционирования возможны переходы из первого состояния во второе с интенсивностью. Граф состояний для рассматриваемого случая представлен на рис. 1.2. В дальнейшем оценим вероятность события А, состоящего в том, что изделие находиться в работоспособном состоянии в момент времени t + t. Очевидно для этого необходимо выполнения двух событий, а именно : события В, состоящего в том, что изделие находиться в первом состоянии в момент t , событие С, состоящего в том, что в течение отрезка t не произойдет отказа. Тогда используя теорему умножения, получим

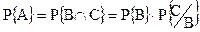(1.1)

Учитывая принятые обозначения соотношение (1.1) можно записать так

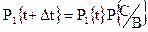(1.2)

С другой стороны, согласно определению λ, вероятность отказа изделия на отрезке Δt при условии его безотказного функционирования до момента t равна λΔt. Отсюда, условная вероятность P{C/B} его безотказного функционирования на отрезке Δt , как вероятность противоположного события будет равна (1 – λΔt).

Таким образом, соотношение (1.2) примет вид

P₁{t + Δt} = P₁{t}(1 – λΔt) (1.3)

После преобразований получим

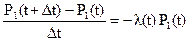(1.4)

Переход к пределу при Δt → 0, приходим к дифференциальному уравнению

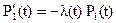(1..5)

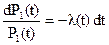или

Интегрируя, получим

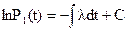(1..6)

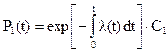Отсюда

(1..7)

где С₁ = Р₁(0) – вероятность исправности изделия в начальный момент времени.

Соотношение (1..7) позволяет оценить надежность изделия при любых заданных λ(t). В частном случае постоянство интенсивности отказа (λ(t) = λ = соnst) выражение (1..7) упростится

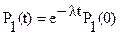(1.8)

Этот случай соответствует так называемому экспоненциальному закону надежности и находит широкое рассмотрение на практике. Действительно для многих технических условий кривая изменений λ(t) имеет «ваннообразный вид» (см. рис. 1.3). Таким образом, весь период функционирования может быть разбит на три участка: период приработки, штатного функционирования и период старения. Как правило, крайние участки не рассматривается при оценке надежности, так как приработочные отказы устраняются при контрольных проверках, а участок старения исключается соответствующим назначением ресурса.

Третья характеристика, среднее время безотказной работы, находиться как математическое ожидание времени отказа

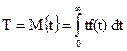(1..9)

где f(t) – плотность распределение времени отказа.

Для экспоненциального закона соотношение (2.9) примет вид

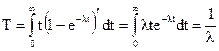(1.10)

Лекция №2

Общая теория надежности.

Общая теория надежности позволяет прогнозировать надежность различных изделий уже на этапе их проектирования, то есть до изготовления готовых образцов. Она основывается на анализе функционирования изделия и выявление условий его отказа. Согласно этой теории в рассмотрение водится функция работоспособности изделия ρ(t) с помощью которой записывается условие работоспособности, выполнение которого гарантирует безотказность изделия.

Например, при оценке вероятности не разрушения элемента конструкции в качестве функции работоспособности можно рассмотреть разность между действующими (σ_д) и допустимыми (σ_доп) напряжениями

ρ(t) = σ_д(t) - σ_доп(t) (1.11)

При этом условие работоспособности примет вид

ρ(t) < 0 ; 0 < t < T (1.12)

где Т – время функционирования изделия.

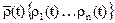Условие работоспособности должно выполняться для каждого момента времени t. В данном случае предполагается, что ρ(t) является случайной функцией времени. В некоторых случаях ρ может не зависеть от времени, то есть является случайной величиной. Однако в наиболее общих ситуациях функция работоспособности надо предполагать векторной функцией . При этом под условием работоспособности понимаются принадлежность этой функции некоторой области допустимых значений Д .

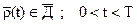(1.13)

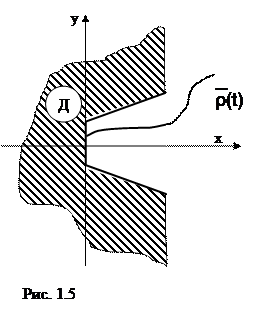
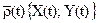В частности, такие ситуации возникают при оценке вероятности безударного движения разделяемых объектов.Для определенности рассмотрим разделение 2х блоков, представленных на рис 1.4. Из анализа процесса разделения было выяснено, что элемент конструкции блока Б не должны достигать опасной зоны блока В, заштрихованной на рисунке. Допустим наибольшую опасность с точки зрения соударения представляют элементы конструкции блока Б, соответствующие т. А и А ́ (см. рис. 1.4). В дальнейшем будем рассматривать относительное движение точки А в системе координат ХУ с началом в т.О, совпадающей в начальный момент с т.А (рис. 1.5). При этом траектория движения т.А не должна пересекать границу области Д , представленных на рисунке. При построении области Д было учтено, что при движении т. А появляется опасность соударения с ней т. А . Таким образом, траектория движения точки А ограничена не только с верху, но и снизу. В данном случае областью допустимых траекторий т.А является область Д (незаштрихованная на рис. 1.5). Поэтому условия работоспособности, с точки зрения безударности разделения, можно представить в виде

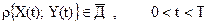(1.14)

Здесь функция работоспособности есть вектор. После определения условия работоспособности надежность изделия оценивается по соотношению

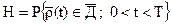
(1.15)

Как показывают результаты исследований произвести оценку вероятности наиболее просто удается только в тех случаях, когда функция работоспособности является случайной величиной. Для случайных функций (даже одномерных) расчет можно произвести только для узких классов случайных процессов. В частности, даже для стационарных, нормальных процессов определить эту вероятность не удается. Поэтому для практических приложений используется приближенное соотношение, дающая достаточно хорошую точность для высоконадежных систем

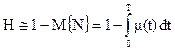(1.16)

где M{N} – среднее число пересечений допустимой области;

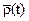μ(t) – среднее число пересечений допустимой области в единицу времени.

Величина μ(t) может быть найдена, если известны характеристики случайного процесса В заключении заметим, что для высоконадежных систем величина μ(t) может быть использована для оценки λ(t). Действительно, согласно формальной теории надежности

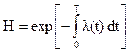(1.17)

Разлагая экспоненту в ряд Тейлора и ограничиваясь линейным членом, получим

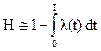(1..18)

Сравнение соотношений (1.17; 1.18) показывает, что можно приближено принять

λ(t) ≈ μ(t) (1.19)

При этом надо помнить, что физический смысл этих параметров совершено различный.

Сложность аналитического представления для μ(t) ограничивает возможность использования этого подхода.

Существенное упрощение расчетов, как в одномерном, так и в многомерном случае дает переход от случайных процессов к случайным величинам. Это оказывается возможным, когда будут найдены моменты времени, соответствующие наиболее тяжелым условиям работы изделия. При этом функция работоспособности анализируется не для всего периода функционирования изделия, а в определенные известные моменты времени. Таким образом, условия работоспособности пишутся в виде

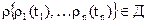(1.20)

где ρ_i(t_i) – некоторые случайные величины.

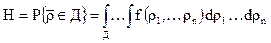Тогда надежность изделия, оцениваемая вероятность выполнения условия (2.20) будет равна

(1.21)

где f(ρ₁… ρ_n) – совместная плотность распределения случайных величин ρ₁, ρ₂,…ρ_n. Для одномерного случая соотношение упроститься:

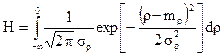(1.22)