Глава 1. множества. числовые множества.

ГЛАВА 1. МНОЖЕСТВА. ЧИСЛОВЫЕ МНОЖЕСТВА.

Комплексные числа

Обозначим через С – множество всех упорядоченных пар действительных чисел 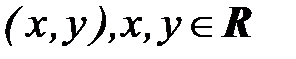. Будем обозначать их 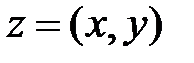. Определим на этом множестве операции сложения и умножения.

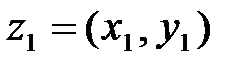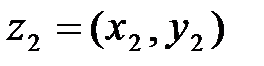Суммой двух упорядоченных пар и назовем упорядоченную пару .

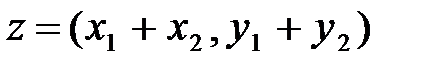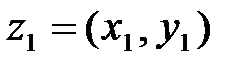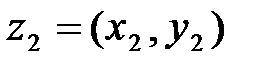Произведением двух упорядоченных пар и назовем упорядоченную пару .

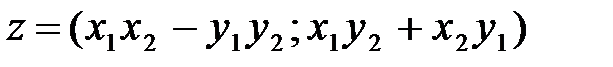Две упорядоченные пары называются равными, если х₁= х₂, y₁= y₂.

Определение 23. Множество С упорядоченных пар z=(х, y), с введенными на нем операциями сложения или умножения, называется множеством комплексных чисел.

Рассмотрим частный случай, возьмем комплексные числа (х₁, 0) и (х₂, 0).

;

;

.

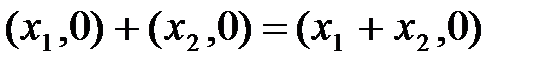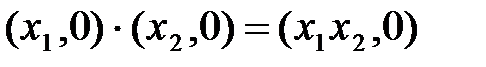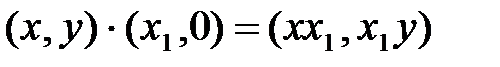Таким образом, в результате сложения и умножения комплексных чисел (х, 0) получили комплексное число такого же вида , а при умножении на (х, y) получили пару, в которой каждый элемент умножается на х₁. Поэтому комплексное число (х, 0) можно отождествить с вещественным числом х. Следовательно, множество R оказывается вложенным в множество комплексных чисел С.

Введем обозначение 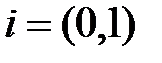. Тогда получим, что

.

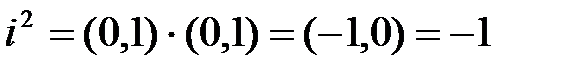Число (1,0)=1 будем называть действительной единицей, а число (0,1)=i -мнимой единицей.

Тогда любое комплексное число можно записать в алгебраическом виде:

, .

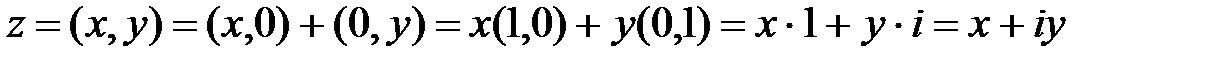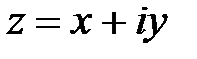Число х называется действительной частью комплексного числа 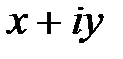, а y – мнимой частью комплексного числа 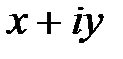. Обозначается .

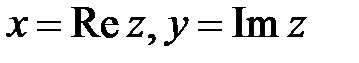Сложение и умножение комплексных чисел обладают свойствами аналогичными свойствам действительных чисел. В частности:

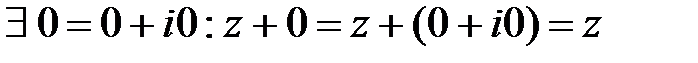- существует нулевой элемент;

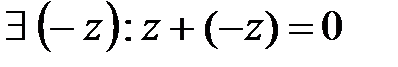- существует противоположный элемент;

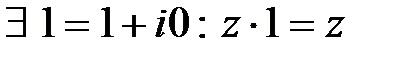- существует единичный элемент;

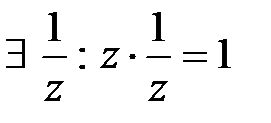- существует обратный элемент, где .

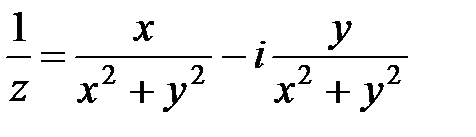Поскольку, существуют нулевой и единичный элемент, то можно ввести операции вычитания и деления комплексных чисел.

Разностью комплексных чисел z₁ и z₂ называется комплексное число z такое, что 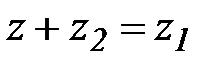. Обозначение:

_.

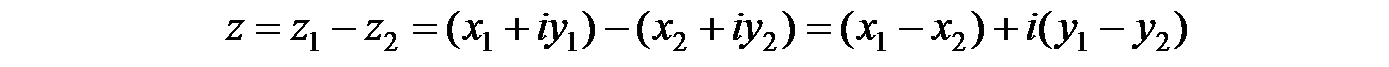Частным от деления 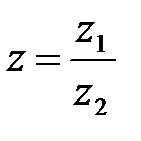называется комплексное число z такое, что :

.

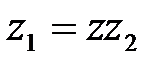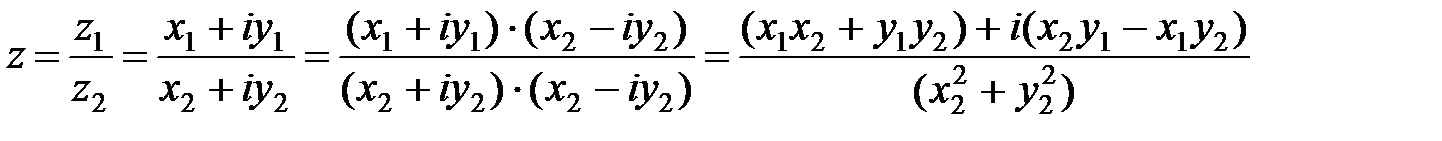Замечание. Из определения комплексного числа в алгебраической форме и правил арифметических действий следует, что при действиях над комплексными числами можно пользоваться правилами действия с алгебраическими двучленами, учитывая, что i²=-1, 1/i=-i.

Комплексное число 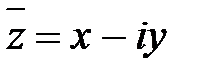называется комплексным сопряженным с комплексным числом 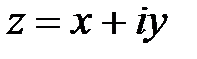. Свойства сопряженных комплексных чисел:

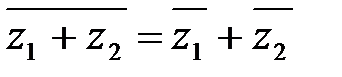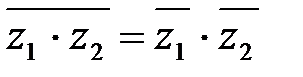1) , 2) , 3) .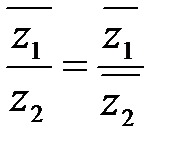

На множестве комплексных чисел можно решать квадратные уравнения с отрицательным дискриминантом. Например,

.

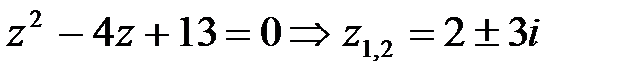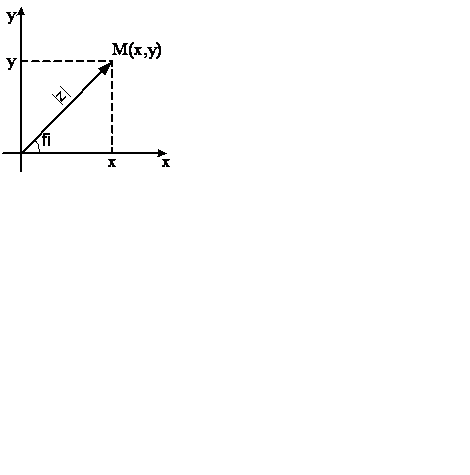
Геометрическая интерпретация комплексных чисел. Каждому комплексному числу z=х+iy на плоскости Oxy соответствует точка М(х,y) и каждой точке на плоскости будет соответствовать одно единственно число.

Число 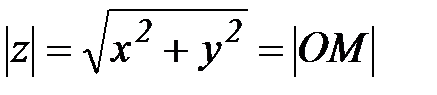называется модулем комплексного числа z. Полярный угол φ между положительным направлением оси Ох и радиусом вектором ОМ называется аргументом комплексного числа z ( ).

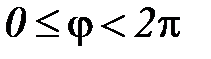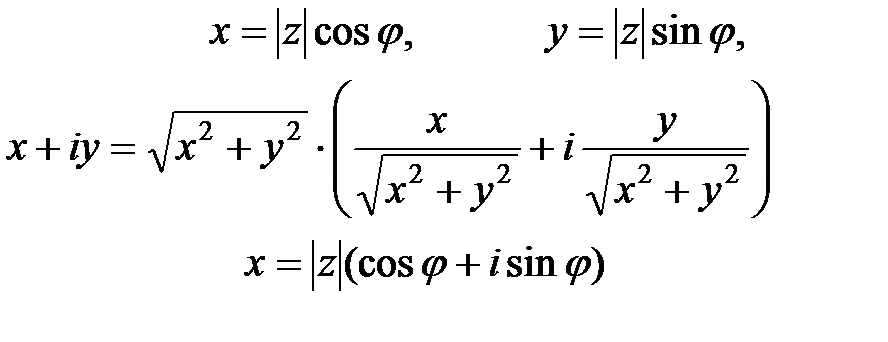
– эта формула называется тригонометрической формой комплексного числа.

Пусть 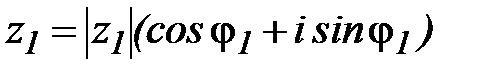, 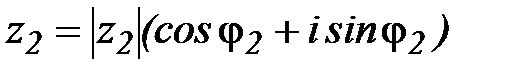– два комплексных числа. Тогда, с помощью соответствующих тригонометрических формул и метода математической индукции легко показать, что справедливы следующие операции над комплексными числами в тригонометрической

,

,

.

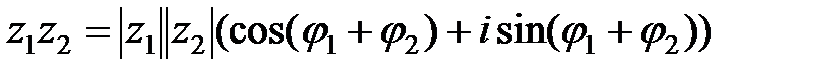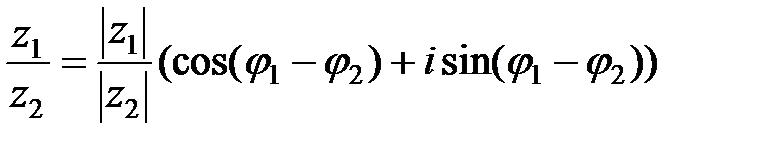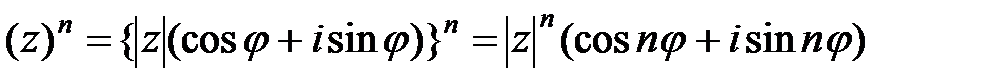1.5. Контрольные вопросы

1.Приведите примеры различных множеств. Приведите пример совпадающих множеств.

2.Сколько можно образовать подмножеств из множества ?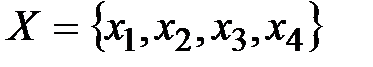

3.Что называется декартовым произведением? Дайте определение отображения множества на множество.

4.Какие числа образуют множество вещественных чисел?

5.Перечислите основные свойства (аксиомы) вещественных чисел.

6.Каким основным свойством отличается множество всех вещественных чисел от множества только рациональных чисел?

7.Какие числовые множества называются промежутками?

8.Из отрезка 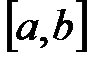удален интервал 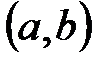. Что осталось?

9.Из отрезка 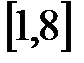удален интервал 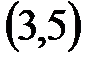. Что осталось? Запишите множество оставшихся чисел с помощью промежутков.

10.Дайте определение ограниченного сверху (снизу) множества X; приведите примеры.

11.Дайте определение точной верхней (нижней) грани ограниченного (снизу) множества 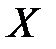; приведите примеры.

12. Применяя правило построения отрицаний, сформулируйте определение неограниченного множества.

13. Привести пример множества, имеющего: а) ровно одну предельную точку; б) ровно шесть предельных точек.

14. Может ли множество, состоящее только из изолированных точек, иметь предельные точки?

15. Является ли замкнутым множеством множество рациональных точек отрезка [0,1]?

16. Привести пример множества, не являющимся ни замкнутым, ни открытым. Привести пример множества, являющегося одновременно открытым и замкнутым.

17.Что означает символическая запись: а) 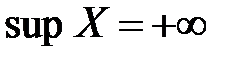; б) ?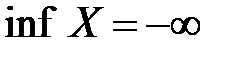

18.Докажите равносильность неравенства 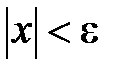и .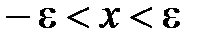

19. Что больше: 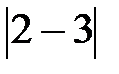или + ?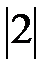

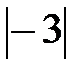20.Найдите 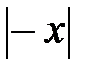, если 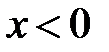. Верно ли, что , если ?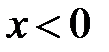

21.Запишите без знака модуля выражение 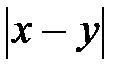, если .

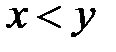22.В чем состоит метод математической индукции?

23.Методом математической индукции докажите, что для любого натурального 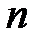справедлива формула .

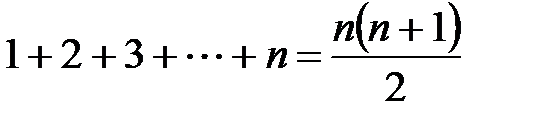24.Что означает запись 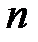! Найдите число 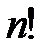для ; .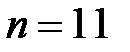

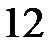25. Может ли 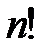кончаться ровно пятью нулями?

26.Запишите формулу бинома Ньютона.

ГЛАВА 1. МНОЖЕСТВА. ЧИСЛОВЫЕ МНОЖЕСТВА.