Получим: ооо, оор, оро, орр.

2.Первый бросок- выпала решка:

Р

О

Р

О

Р

О

Р

Получим: РОО, РОР, РРО, РРР.

Всего случаев :8 благоприятных исходов:4 (ОРР, РОР,РРО,РРР)

Р=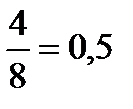

Ответ:0,5

7.Игральный кубик бросают 2 раза. С какой вероятностью выпавшие числа будут отличаться на 3? Ответ округлите до сотых.

Решение:

Закрасим ячейки, где числа отличаются на 3, их шесть. Р= 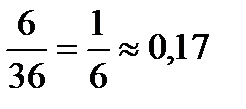Ответ. 0,17

8.В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.

Решение:

Закрасим ячейки, где сумма равна 7, их шесть. Р= .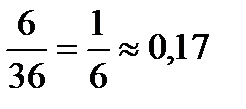

Ответ. 0,17

9.Какова вероятность того, что случайно выбранное число будет делиться нацело на 195? Ответ округлить до тысячных.

Решение.

Количество трёхзначных чисел: 999-99=900. Количество чисел, делящихся на 195: 5 (195, 195∙2, 195∙3, 195∙4. 195∙5=985). Р=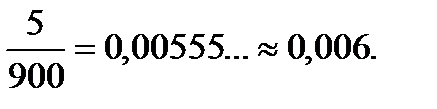

Ответ.0,006.

II

ЗАДАЧИ, В КОТОРЫХ ИСПОЛЬЗУЮТСЯ СВОЙСТВА ВЕРОЯТНОСТЕЙ.

Сумма противоположных событий равна 1.

Р(А)+Р(В)=1

1. Почти одновременно 5 человек, в том числе Петя, заказали по телефону пиццы, все разных видов. Оператор перепутал 3 и 4 заказы. С какой вероятностью Пете привезут его пиццу?

Решение: Найдём вероятность противоположного события, т.е., что Пете привезут не его пиццу: Р= 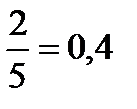Вероятность противоположного события:

1-0,4=0,6.

Ответ. 0,6.

ПРАВИЛО СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ

Р(А+В)= Р(А)+Р(В)

Вероятность одного из интересующих нас результатов эксперимента равна сумме вероятностей каждого из этих результатов, если эти результаты несовместимымежду собой.

Несовместимыми называются такие события, которые в рассматриваемом эксперименте не могут произойти одновременно.

Если случайные события совместимы, т.е. могут произойти одновременно, то правило сложения применять нельзя.

1. Ученик решил сделать прогноз своей успеваемости по математике, изучив свои отметки за 7 класс. Результаты его исследования помещены в таблице.

Отметка	Количество отметок	Примерная вероятность получения отметок
5(отлично)		0,21
4(хорошо)		0,41
3(удовлетворительно)		0,34
2(неудовлетворительно)		0,04

Какова вероятность того, что очередной ответ ученика будет оценён на «4» или «5»?

Решение.

Если не учитывать особые обстоятельства ( сложность темы, состояние здоровья и т.д.) , то вероятность можно оценить так :всего ученик получил 188 отметок, из них ответов на «4» и «5» было 39+78. И т.к. получение оценок одним и тем же учеником за один и тот же ответ – несовместимые события, то вероятность получить «хорошо» или «отлично»

Р= .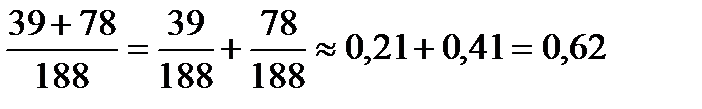

Ответ.0,62.

2. В лотерее выпущено 100000 билетов и установлены: 1 выигрыш в 100000р., 10 выигрышей по 10000р., 100 выигрышей по 1000р., 1000 выигрышей по 100р., и 5000 выигрышей по 50р. Человек купил один лотерейный билет . Какова вероятность того, что он выиграет.

Решение.

Так как куплен один билет, то каждый выигрыш− несовместимые события. Найдём вероятность события: Р=

Ответ. 0,06111.

3).Если события А и В независимы, то вероятность наступления обеих событий вычисляется по формуле: Р(АВ)= Р(А)∙Р(В).

1.Двое военнослужащих на учениях независимо друг от друга проходят полосу препятствий. Для первого вероятность пройти ее равна 0,8, а для второго 0,5. Найдите вероятность того, что они оба не пройдут это испытание.

Решение:

Вероятность того, что первый не пройдёт препятствие: 1-0,8=0,2, а второго :1-0,5= 0,5. Так как эти события независимы друг от друга, то Р= 0,2∙0,5=0,1.

Ответ: 0,1

2.Стрелок стреляет в мишень три раза. Вероятность попадания при каждом выстреле равна 0,9.Найдите вероятность того, что стрелок промахнётся все три раза.

Решение.Вероятность того, что стрелок промахнётся: 1-0,9 =0,1.Так как три выстрела─ независимые друг от друга события, то Р = 0,1∙0,1∙0,1= 0,001.

Ответ. 0,001.

3.Вероятность того, что Андрей сдаст экзамен по математике равна 0,99, а вероятность того, что он сдаст экзамен по русскому языку . равна 0,98. Найдите вероятность того, что он сдаст оба эти экзамена.

Решение. Так как эти события независимы друг от друга, то Р=0,99∙0,98=0,9702.

Ответ.0,9702.

4.Биатлонист 5 раз стреляет по мишеням. Вероятность попадания при одном выстреле равна 0,8.Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два раза промахнулся. Результат округлите до сотых.

Решение. события: попал при первом выстреле, при втором выстреле и т.д. независимы. Вероятность каждого попадания равна 0,8. Значит вероятность каждого промаха равна1-0,8= 0,2.Воспользуемся формулой умножения вероятностей независимых событий. Получаем, что событие: А= {попал;попал; попал; промахнулся; промахнулся} имеет вероятность Р=0,8∙0,8∙0,8∙0,2∙0,2=0,02048=0,02.

Ответ.0,02

5. Вероятность того, что телевизор прослужит больше 5 лет равна 0,92.

Вероятность того, что телевизор прослужит больше 10 лет равна 0,39.Найдите вероятность того, что он прослужит больше 5, но меньше 10 лет.

Решение.

0,92- 0,39=0,53.

Ответ.0,53