Задачи, в которых можно выписать все элементарные события эксперимента.
ЗАДАЧИ, В КОТОРЫХ МОЖНО ВЫПИСАТЬ ВСЕ ЭЛЕМЕНТАРНЫЕ СОБЫТИЯ ЭКСПЕРИМЕНТА.
| Р = |
| Число благоприятствующих событий |
| Общее число событий |
1.Проводится жеребьёвка Лиги Чемпионов. На первом этапе жеребьёвки восемь команд, среди которых команда «Барселона», распределились случайным образом по восьми игровым группам — по одной команде в группу. Затем по этим же группам случайным образом распределяются еще восемь команд, среди которых команда «Зенит».
Найдите вероятность того, что команды «Барселона» и «Зенит» окажутся в одной игровой группе.
Решение:
После первого этапа жеребьевки команда "Барселона" попадет в некоторую группу, фиксируем ее номер. Теперь задача сводится к тому, чтобы определить вероятность того, что команда "Зенит" попадет в эту же группу.
Всего групп 8. Попадание "Зенита" только в одну из них является благоприятным исходом. Следовательно, вероятность равна 1:8=0,125.
Ответ. 0,125
2.Жюри конкурса народной песни собирается прослушать в первые два дня по 15 человек, а в третий день — оставшихся 20. С какой вероятностью артист Петров выступит во второй день, если порядок выступлений участников определяется жребием?
Решение.Во второй день выступало 15 человек, а всего – 50 человек.
Р=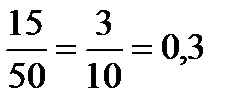 
Ответ 0,3
2. Учительница разбила класс на 8 групп по 4 человека, выдав каждой группе тему доклада для следующего урока и назначив старшего в группе. Антон - старший в некоторой группе - накануне весь вечер играл в футбол, поэтому его группа доклад не подготовила. Учительница может вызывать для презентации доклада любого учащегося, кроме старших по группам. Какова вероятность, что вызовут школьника из группы Антона?
Решение:Количество учеников, которое может вызвать учительница:8∙3=24. Трое из группы Антона. Р=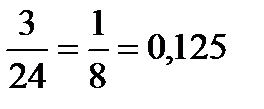 
Ответ: 0,125.
3. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 спортсменов, среди которых 10 участников из России, в том числе Григорий Поддубный.
Найдите вероятность того, что в первом туре Григорий Поддубный будет играть с каким-либо спортсменом из России?
Решение: пусть Поддубный попал в одну из групп, тогда для остальных 9 Россиян осталось 75 мест. Р=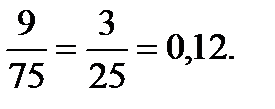 
Ответ: 0,12
4. В группе иностранных туристов51 человек, среди них два француза. Для посещения маленького музея группу случайным образом делят на три подгруппы, одинаковые по численности. Найдите вероятность того, что французы окажутся в одной подгруппе.
Решение. В каждой подгруппе 17 человек. Будем считать, что один француз уже занял место в какой-то подгруппе. Надо найти вероятность того, что второй француз окажется в той же подгруппе. Для второго француза осталось 50 мест , а в подгруппе -16 мест. Размещения туристов случайны, значит события равновозможны. Поэтому вероятность того, что второй француз попадёт в ту же подгруппу : Р=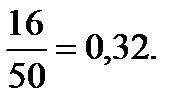 
Ответ: 0,32.
5.Петя подкинул три монеты. С какой вероятностью они выпали одной стороной?
Решение:
Орёл-О, решка-Р. Все возможные случаи:
ООО, ООР, ОРО, ОРР, РРР, РОР, РРО, РОО. Их восемь. Благоприятных исходов два. Р=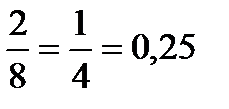 
Ответ: 0, 25
6. Симметричную монету бросают три раза. Найдите вероятность того, что орлов выпадет больше, чем решек.
Решение:
Нарисуем «дерево»:1. Первый бросок- выпал орёл:
| О |
| О |
| Р |
| О |
| Р |
| О |
| Р |
Ответ:0,5
7.Игральный кубик бросают 2 раза. С какой вероятностью выпавшие числа будут отличаться на 3? Ответ округлите до сотых.
Решение:
Закрасим ячейки, где числа отличаются на 3, их шесть. Р=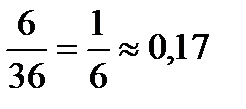 
Ответ. 0,17
8.В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.
Решение:
Закрасим ячейки, где сумма равна 7, их шесть. Р= .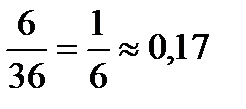
Ответ. 0,17
9.Какова вероятность того, что случайно выбранное число будет делиться нацело на 195? Ответ округлить до тысячных.
Решение.
Количество трёхзначных чисел: 999-99=900. Количество чисел, делящихся на 195: 5 (195, 195∙2, 195∙3, 195∙4. 195∙5=985). Р=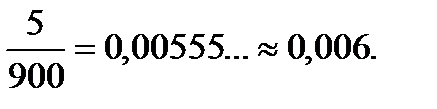 
Ответ.0,006.
II
Ответ. 0,6.
Ответ.0,62.
2. В лотерее выпущено 100000 билетов и установлены: 1 выигрыш в 100000р., 10 выигрышей по 10000р., 100 выигрышей по 1000р., 1000 выигрышей по 100р., и 5000 выигрышей по 50р. Человек купил один лотерейный билет . Какова вероятность того, что он выиграет.
Решение.
Так как куплен один билет, то каждый выигрыш− несовместимые события. Найдём вероятность события: Р= 
Ответ. 0,06111.
3).Если события А и В независимы, то вероятность наступления обеих событий вычисляется по формуле: Р(АВ)= Р(А)∙Р(В).
1.Двое военнослужащих на учениях независимо друг от друга проходят полосу препятствий. Для первого вероятность пройти ее равна 0,8, а для второго 0,5. Найдите вероятность того, что они оба не пройдут это испытание.
Решение:
Вероятность того, что первый не пройдёт препятствие: 1-0,8=0,2, а второго :1-0,5= 0,5. Так как эти события независимы друг от друга, то Р= 0,2∙0,5=0,1.
Ответ: 0,1
2.Стрелок стреляет в мишень три раза. Вероятность попадания при каждом выстреле равна 0,9.Найдите вероятность того, что стрелок промахнётся все три раза.
Решение.Вероятность того, что стрелок промахнётся: 1-0,9 =0,1.Так как три выстрела─ независимые друг от друга события, то Р = 0,1∙0,1∙0,1= 0,001.
Ответ. 0,001.
3.Вероятность того, что Андрей сдаст экзамен по математике равна 0,99, а вероятность того, что он сдаст экзамен по русскому языку . равна 0,98. Найдите вероятность того, что он сдаст оба эти экзамена.
Решение. Так как эти события независимы друг от друга, то Р=0,99∙0,98=0,9702.
Ответ.0,9702.
4.Биатлонист 5 раз стреляет по мишеням. Вероятность попадания при одном выстреле равна 0,8.Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два раза промахнулся. Результат округлите до сотых.
Решение. события: попал при первом выстреле, при втором выстреле и т.д. независимы. Вероятность каждого попадания равна 0,8. Значит вероятность каждого промаха равна1-0,8= 0,2.Воспользуемся формулой умножения вероятностей независимых событий. Получаем, что событие: А= {попал;попал; попал; промахнулся; промахнулся} имеет вероятность Р=0,8∙0,8∙0,8∙0,2∙0,2=0,02048=0,02.
Ответ.0,02
5. Вероятность того, что телевизор прослужит больше 5 лет равна 0,92.
Вероятность того, что телевизор прослужит больше 10 лет равна 0,39.Найдите вероятность того, что он прослужит больше 5, но меньше 10 лет.
Решение.
0,92- 0,39=0,53.
Ответ.0,53
ЗАДАЧИ, В КОТОРЫХ МОЖНО ВЫПИСАТЬ ВСЕ ЭЛЕМЕНТАРНЫЕ СОБЫТИЯ ЭКСПЕРИМЕНТА.
| Р = |
| Число благоприятствующих событий |
| Общее число событий |
1.Проводится жеребьёвка Лиги Чемпионов. На первом этапе жеребьёвки восемь команд, среди которых команда «Барселона», распределились случайным образом по восьми игровым группам — по одной команде в группу. Затем по этим же группам случайным образом распределяются еще восемь команд, среди которых команда «Зенит».
Найдите вероятность того, что команды «Барселона» и «Зенит» окажутся в одной игровой группе.
Решение:
После первого этапа жеребьевки команда "Барселона" попадет в некоторую группу, фиксируем ее номер. Теперь задача сводится к тому, чтобы определить вероятность того, что команда "Зенит" попадет в эту же группу.
Всего групп 8. Попадание "Зенита" только в одну из них является благоприятным исходом. Следовательно, вероятность равна 1:8=0,125.
Ответ. 0,125
2.Жюри конкурса народной песни собирается прослушать в первые два дня по 15 человек, а в третий день — оставшихся 20. С какой вероятностью артист Петров выступит во второй день, если порядок выступлений участников определяется жребием?
Решение.Во второй день выступало 15 человек, а всего – 50 человек.
Р=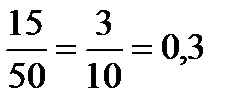
Ответ 0,3
2. Учительница разбила класс на 8 групп по 4 человека, выдав каждой группе тему доклада для следующего урока и назначив старшего в группе. Антон - старший в некоторой группе - накануне весь вечер играл в футбол, поэтому его группа доклад не подготовила. Учительница может вызывать для презентации доклада любого учащегося, кроме старших по группам. Какова вероятность, что вызовут школьника из группы Антона?
Решение:Количество учеников, которое может вызвать учительница:8∙3=24. Трое из группы Антона. Р=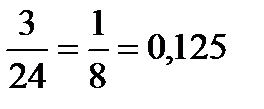
Ответ: 0,125.
3. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 спортсменов, среди которых 10 участников из России, в том числе Григорий Поддубный.
Найдите вероятность того, что в первом туре Григорий Поддубный будет играть с каким-либо спортсменом из России?
Решение: пусть Поддубный попал в одну из групп, тогда для остальных 9 Россиян осталось 75 мест. Р=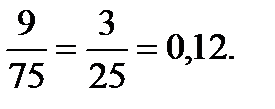
Ответ: 0,12
4. В группе иностранных туристов51 человек, среди них два француза. Для посещения маленького музея группу случайным образом делят на три подгруппы, одинаковые по численности. Найдите вероятность того, что французы окажутся в одной подгруппе.
Решение. В каждой подгруппе 17 человек. Будем считать, что один француз уже занял место в какой-то подгруппе. Надо найти вероятность того, что второй француз окажется в той же подгруппе. Для второго француза осталось 50 мест , а в подгруппе -16 мест. Размещения туристов случайны, значит события равновозможны. Поэтому вероятность того, что второй француз попадёт в ту же подгруппу : Р=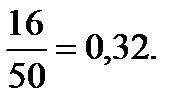
Ответ: 0,32.
5.Петя подкинул три монеты. С какой вероятностью они выпали одной стороной?
Решение:
Орёл-О, решка-Р. Все возможные случаи:
ООО, ООР, ОРО, ОРР, РРР, РОР, РРО, РОО. Их восемь. Благоприятных исходов два. Р=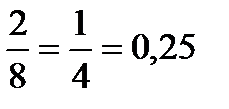
Ответ: 0, 25
6. Симметричную монету бросают три раза. Найдите вероятность того, что орлов выпадет больше, чем решек.
Решение:
Нарисуем «дерево»:1. Первый бросок- выпал орёл:
| О |
| О |
| Р |
| О |
| Р |
| О |
| Р |