Прохождение случайного сигнала через линейную систему
Для примера возьмем систему автоматического регулирования частоты (САРЧ) вращения вала дизеля без управления по возмущению (см. рис.6.26) и в качестве возмущающего воздействия используем нормально распределенный сигнал (блок Random Number) с параметрами: математическое ожидание Mean = 0,5; дисперсия Variance = 0,01; стартовое значение Initial seed = 0 и время дискретизации Sample time = 0 (непрерывный сигнал). Кроме того, необходимо добавить регистрирующие блоки, передающие информацию в рабочую область (блок To Workspace). Структурная схема показана на рис. 7.3.
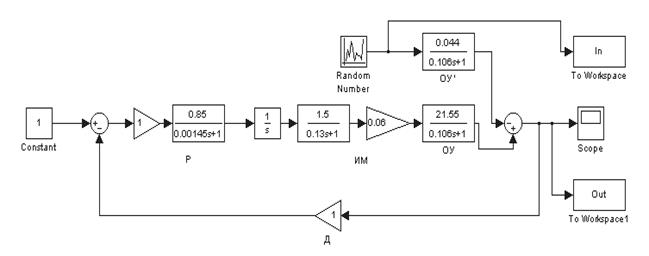
Рис.7.3. Структурная схема системы стабилизации угловой скорости турбогенератора со случайным возмущающим воздействием
Блок To Workspace служит для регистрации случайного сигнала, подаваемого на вход системы, а блок To Workspace1 – для регистрации выходного сигнала. Блок To Workspace имеет следующие параметры (рис.7.4):
1) Variable name – имя переменной, в которой будут сохраняться результаты;
2) Limit data points to last – предел количества точек запоминаемой величины (inf – бесконечное число точек);
3) Decimation – разрядность хранимой величины;
4) Sample time – шаг времени, через который происходит сохранение значений;
5) Save format – формат, в котором происходит сохранение, может быть: Structure with time – структура с временем; Structure – структура, Array – массив.
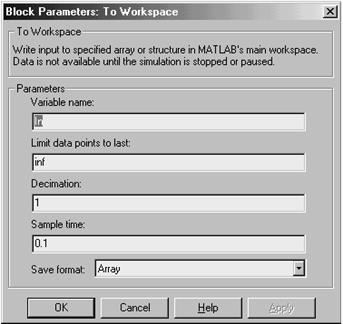
Рис.7.4. Настройка блока To Workspace
В параметрах обоих блоков устанавливаем: Sample time = 0,1 и Save format – Array, параметры Limit data points to last и Decimation оставляем без изменений. Имена переменных: для входного блока – In, а для выходного – Out, при этом имена переменных появляются на изображении блока на схеме (см. рис.7.3).
Время моделирования устанавливаем (в меню окна модели Simulation > Simulation Parameters… > Stop time), равным 50 с, этого достаточно, чтобы определить характеристики случайного сигнала.
Далее необходимо запустить процесс моделирования (в меню окна модели Simulation > Start) и выполнить следующие действия:
1. В основном окне MATLAB выполнить следующие команды:
t=0:0.1:50; – задаем вектор времени (от 0 до 50 с, с шагом 0,1);
plot(t,In) – построить график случайного процесса, подаваемого в качестве возмущающего воздействия.
Оператор “;” стоящий после команды, позволяет отключить вывод результатов этой команды на экран.
2. После выполнения этих команд появится окно Figure No.1 (рис.7.5), в котором и отображается график случайного сигнала. Для того чтобы получить характеристики этого сигнала, необходимо из меню окна Figure No.1 выполнить: Tools > Data Statistics, после чего появится новое окно - Data Statistics-1, в котором отображаются интересующие нас статистические параметры отдельно по осям графика (X – ось времени, Y – ось ординат случайного сигнала):
· min – минимальное значение;
· max – максимальное значение;
· mean – математическое ожидание;
· std – среднеквадратическое отклонение (квадратный корень из дисперсии, значение которой задано в параметрах блока Random Number).
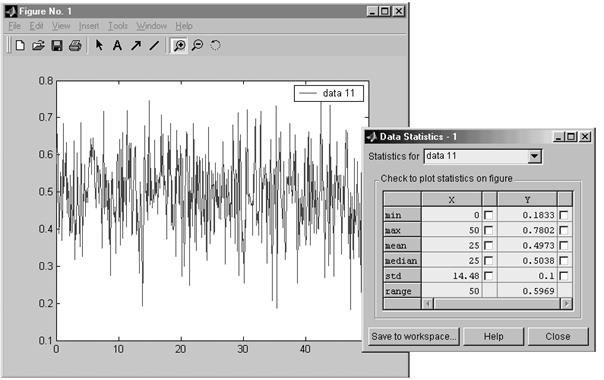
Рис.7.5. График случайного процесса и его параметры на входе в САРЧ
При нажатии на квадратик напротив любой из величин появляются ли-
нии на графике, отображающие эту величину.
Нас интересуют параметры случайного сигнала, поданного на вход системы, то есть ось Y. Можно убедиться, что математическое ожидание близко к 0,5 и составляет 0,4973 (при увеличении количества точек оно стремится к заданному, равному 0,5) и среднеквадратическое отклонение, равное квадратному корню из дисперсии, составляет 0,1 ( 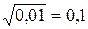 ).
).
Из-за особенностей пакета Data Statistics необходимо проверять значение среднеквадратического отклонения, для этого в основном окне MATLAB выполняем команду std(In,1), при этом выдается значение 0,9999, что очень близко к заданной его величине.
3. Для анализа выходного сигнала необходимо выполнить следующие команды:
t1=3:0.1:50; – задаем вектор времени (от 3 до 50 с, с шагом 0,1), так как переходный процесс по возмущению составляет 1,37 с, то анализируем выход без влияния переходного процесса по управлению и берем не менее чем двукратный запас по времени;
Out1=Out(30:500); – вычленяем из выходного массива выходной сигнал, без влияния переходного процесса по управлению, то есть отбрасываем 30 первых точек (первый операнд в скобках − это начальная точка, равная начальному времени из предыдущей команды, деленному на шаг времени, второй операнд – конечная точка, равная времени моделирования, деленному на шаг времени);
plot(t1,Out1) – построить график случайного процесса на выходе из САРЧ;
std(Out1,1) – уточняем значение среднеквадратического значения.
4. В окне Figure No.1 появляется график случайного процесса на выходе из САРЧ, а в окне Data Statistics – характеристики этого процесса, без влияния переходного процесса по управлению (рис.7.6).
Получены следующие характеристики:
· минимальное значение равно 0,9978;
· максимальное значение равно 1,002;
· математическое ожидание равно 1;
· среднеквадратическое отклонение равно 6,7556×10-4 (уточненное значение);
· дисперсия равна (6,7556×10-4)2 = 4,5638×10-7.
Таким образом, в качестве возмущающего сигнала использовался случайный сигнал с параметрами: математическое ожидание, равное 0,5, то есть момент нагрузки на валу двигателя в среднем равен половине от максимально возможного; минимальный момент нагрузки равен 0,1833 от максимально возможного и максимальный момент нагрузки равен 0,7802 от максимально возможного.
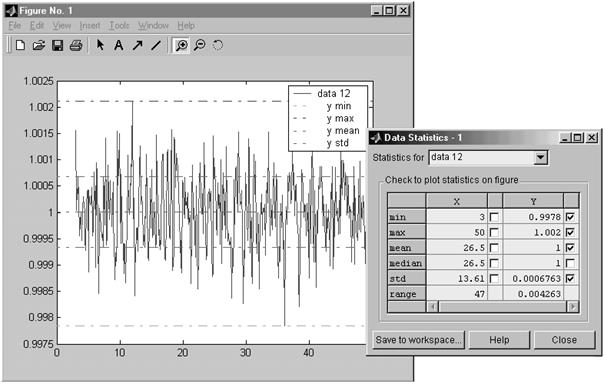
Рис.7.6. График случайного процесса и его параметры на входе в САРЧ
При прохождении возмущающего сигнала через систему он изменяется и частота вращения от возмущающего воздействия в среднем не изменяется, так как математическое ожидание случайного процесса на выходе равно единице. Но в целом частота вращения изменяется от минимального значения, равного 0,9978, до максимального значения, равного 1,002, от номинальной частоты вращения.
Дисперсия случайного сигнала уменьшилась с 0,1 до 4,5638×10-7, то есть в 219115 раз. Таким образом, САРЧ служит своеобразным фильтром для случайного сигнала, проходящего через нее.
Для получения плотности вероятности распределения случайного сигнала служит команда histfit(Variable name, N), где операнд Variable name указывает на имя переменной, а операнд N устанавливает количество интервалов гистограммы.
Для нашего примера значения этих операндов:
1) для входного сигнала – имя переменной In, количество интервалов гистограммы, равное времени моделирования, деленному на шаг (500). Команда выглядит следующим образом: histfit(In,500) (рис.7.7);
2) для выходного сигнала – имя переменной Out1 (без переходного процесса по управлению), количество интервалов гистограммы, равное времени моделирования, деленному на шаг, за вычетом отбрасываемых точек (470). Команда выглядит следующим образом: histfit(Out1,470) (рис. 7.8).
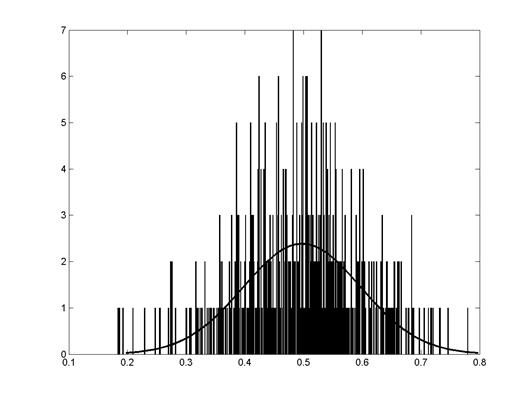
Рис.7.7. Плотность вероятности распределения случайного
Сигнала на входе в САРЧ
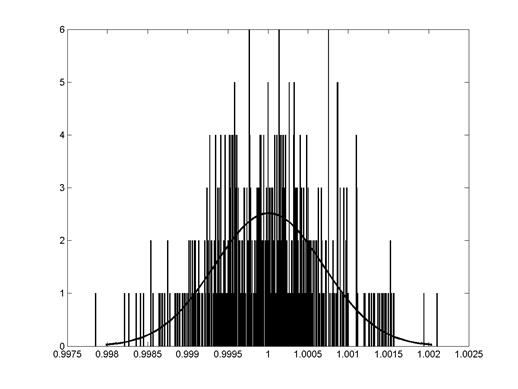
Рис.7.8. Плотность вероятности распределения случайного
Сигнала на выходе из САРЧ
