Общая методика анализа линейных систем

Автоматического управления

Для проведения анализа произвольной системы автоматического управления необходимо выполнить следующие действия (в качестве примера далее приводится анализ системы стабилизации угловой скорости турбогенератора).

1. Построить принципиальную или кинематическую схему САУ (рис.5.15) и выделить на ней отдельные функциональные элементы.

В схему входят следующие элементы: Т – турбина (объект управления); МП – механическая передача; ЦБМ – центробежный маятник (выполняет функции датчика, определяющего действительную угловую скорость, задатчика угловой скорости и сумматора, вычисляющего ошибку регулирования); ГУ – гидроусилитель; ГСП – гидравлический сервопривод; ПВК – паровпускной клапан с регулируемым расходом; Г – генератор, приводимый во вращение турбиной.

Некоторой установившейся нагрузке генератора соответствует определенная угловая скорость турбины, положение грузов ЦБМ и поршня ГСП, а также величина открытия ПВК. Если нагрузка уменьшится, угловая скорость турбины возрастет, грузы ЦМБ, а вместе с ними и муфта переместятся вверх (z). Переместится и золотник ГУ (s₁), поршень ГСП пока остается неподвижным (s₂ = 0), так как закрыты окна ГУ. Он приоткроет дос-

Рис.5.15. Принципиальная схема системы стабилизации угловой

Скорости турбогенератора

туп рабочего тела (жидкости) в верхнюю полость ГСП, поршень которого начнет перемещаться вниз и прикроет ПВК, который, в свою очередь, уменьшит подачу пара в турбину, вследствие чего угловая скорость турбины уменьшится. Одновременно, из-за наличия жесткой обратной связи между ГСП и ГУ (рычаг, связывающий ГСП, ГУ и ЦБМ), золотник ГУ переместится вниз и прикроет окна ГУ и движение поршня ГСП прекратится. Система вновь будет в некотором установившемся режиме.

Таким образом, система стабилизации угловой скорости турбогенератора является замкнутой следящей системой (регулирование по отклонению). Главная обратная связь системы представлена механической передачей (МП). Также в системе имеется местная жесткая отрицательная обратная связь, охватывающая ГСП.

2. На основе принципиальной или кинематической схемы составить функциональную схему системы (рис.5.16).

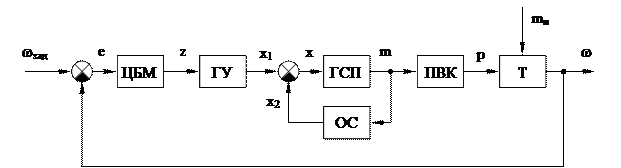
Рис.5.16. Функциональная схема системы стабилизации угловой

Скорости турбогенератора

На функциональной схеме показаны следующие сигналы: e – ошибка регулирования (отклонение); z – перемещение муфты ЦБМ; х₁ – перемещение золотника ГУ от ЦБМ; х₂ – перемещение золотника ГУ от ГСП; х – суммарное перемещение золотника ГУ; m – перемещение ПВК, пропорциональное перемещению поршня ГСП; p – давление пара на входе в турбину; w – угловая скорость вращения вала турбины; w_зад – заданная угловая скорость вращения вала турбины; m_н – момент нагрузки на валу турбины.

В любой момент времени с помощью сумматора выполняется сравнение заданного и фактического значений угловой скорости вращения вала турбины (вычисляется ошибка регулирования):

e = w_зад − w. (5.5)

Если ошибка регулирования не равна нулю, то происходят следующие перемещения: муфты ЦБМ (z), золотника ГУ (s), поршня ГСП (m), штока ПВК, вследствие чего изменяется давление на входе в турбину (p). Знаки перемещений зависят от знака ошибки регулирования.

В результате чего изменяется фактическая угловая скорость вращения вала турбины и ошибка регулирования стремится к нулю.

Таким образом, в данной схеме:

● ЦБМ исполняет функции: датчика угловой скорости, задатчика и сумматора (сравнивающего элемента);

● ГУ и ГСП являются ПИ-регулятором;

● ПВК является исполнительным устройством, изменяющим подачу пара в турбину;

● турбина Т является объектом управления.

3. Произвести математическое описание элементов функциональной схемы в виде передаточных функций.

Уравнения отдельных элементов в отклонениях имеют следующий вид:

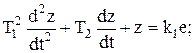
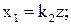
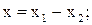
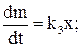(5.6)

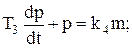
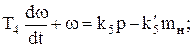
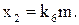
Далее преобразуем уравнения в передаточные функции:

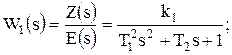
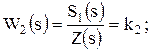
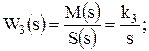
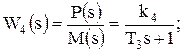(5.7)

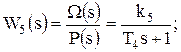
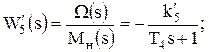
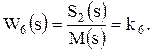
Числовые значения параметров: k₁ = 10; k₂ = 0,6; k₃ = 2; k₄ = 0,8; k₅ = 1; k`₅ = 0,2; k₆ = 0,4; Т₁² = 0,001 с²; Т₂ = 0,2 с; Т₃ = 5 с; Т₄ = 0,3 с.

4. На основании функциональной схемы строим структурную схему системы (рис.5.17).

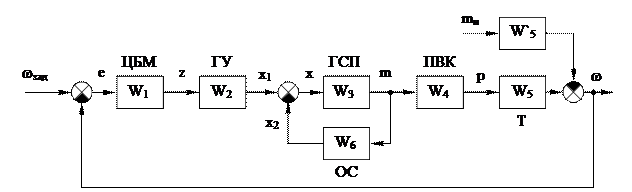
Рис.5.17. Структурная схема системы стабилизации угловой

Скорости турбогенератора

Теперь, имея структурную схему системы и зная передаточные функции и числовые значения входящих в них коэффициентов, можно переходить непосредственно к анализу системы с помощью пакета Simulink.

5. Собрать структурную схему в пакете Simulink, используя типовые блоки (процесс сборки схемы и типовые блоки подробно описаны в третьей главе данного учебного пособия).

Поскольку в системе стабилизации угловой скорости турбогенератора кроме управляющего воздействия существует еще и возмущающее воздействие в виде нагрузки на валу турбины, следует провести анализ не только по управляющему, но и по возмущающему воздействию.

Для анализа системы по управляющему воздействию точки входа и выхода (Input and Output point) должны быть расположены так как, показано на рис.5.3 и 5.4, то есть точка входа располагается в месте приложения управляющего воздействия, а выхода – в месте расположения выходного сигнала.

Анализ системы по различным воздействиям производится раздельно. Сначала надо убедиться в устойчивости системы, получить показатели устойчивости и качества по управляющему воздействию, а затем оценить влияние возмущения на переходный процесс системы. Анализ устойчивости по возмущающему воздействию не производится, так как возмущающее воздействие не входит в передаточную функцию системы по управляющему воздействию и, следовательно, не влияет на устойчивость системы в целом.

6. Используя разомкнутую структурную схему системы, без возмущающего воздействия (рис.5.4) с помощью частотного критерия Найквиста (см. рис.5.5 и 5.6) сделать вывод об устойчивости системы по управляющему воздействию и получить значения запасов устойчивости (см. рис.5.8 и 5.9).

Для анализируемой системы можно сделать вывод об ее устойчивости, так как АФЧХ разомкнутой системы не охватывает точку (−1, j0) и частота среза (w_с = 1,2 рад/с) меньше частоты фазового сдвига (w_p = 1,39 рад/с).

Запасы устойчивости:

- по амплитуде DL = 2,37 дБ;

- по фазе Dj = 9,75 °.

7. Используя замкнутую структурную схему системы без возмущающего воздействия (см. рис.5.3), получить показатели качества.

Для анализируемой системы показатели качества:

- установившееся значение выходной величины y_уст = 0,923;

- ошибка регулирования e_ст = 0,923 − 1 = − 0,077 (так как на входе единичное ступенчатое воздействие, то y_зад = 1);

- перерегулирование s = 76,3 %;

- время регулирования t_р = 36,9 с.

8. Провести анализ влияния возмущающего воздействия на переходный процесс. Для этого необходимо добавить в структурную схему звено с передаточной функцией W`<sub>5</sub> (отрицательный знак в передаточной функции W`₅ учитывается с помощью сумматора), источник единичного ступенчатого воздействия и разместить еще одну точку входа (Input Point1) (рис.5.18).

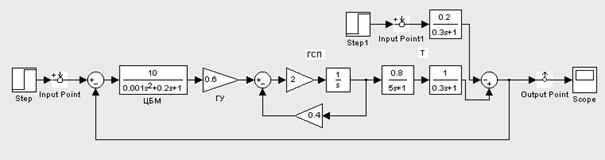
Рис.5.18. Структурная схема системы стабилизации угловой скорости

турбогенератора с возмущающим воздействием

При этом система анализируется также с использованием LTI Viewer, но в его окне теперь содержится два графика переходных процессов (рис.5.19) – от управляющего (левый) и от возмущающего (правый).

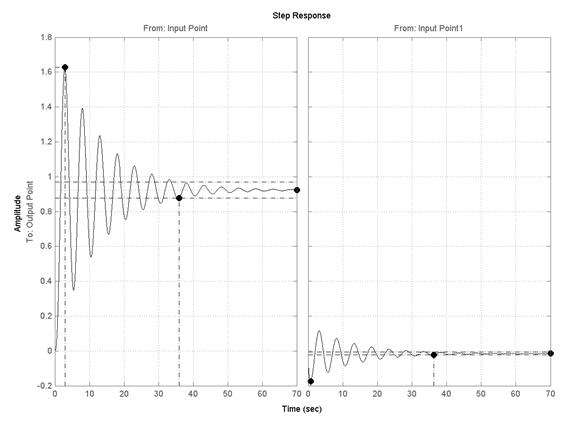
Рис.5.19. Анализ влияния возмущающего воздействия на

переходный процесс

Для численной оценки используются такие же критерии качества (кроме перерегулирования), как и для управляющего воздействия. Для анализируемой системы (снимается с соответствующих точек на правом графике рис. 5.19) показатели качества имеют следующие значения:

- максимальное значение y_max = − 0,174;

- длительность переходного процесса t_пп = 36,3 с;

- установившееся значение y_уст = − 0,0154;

- статическая ошибка e_ст = y_уст - y_зад = − 0,0154 - 0 = − 0,0154.

При отработке системой автоматического управления возмущающего воздействия эта система должна стремиться к тому, чтобы возмущающее воздействие не влияло на статический режим, то есть e_ст должна быть как можно меньше или, в идеале, равна нулю (поэтому для возмущающего воздействия y_зад = 0). Для этого используют различные способы коррекции (управление по отклонению и т.д.).

В рассматриваемом примере в результате приложения к системе одновременно управляющего и возмущающего воздействий установившееся значение выходного сигнала будет равно сумме значений y_уст для этих воздействий: y_устS = 0,923 – 0,0154 = 0,9076. Таким же образом можно подсчитать и суммарную статическую ошибку e_стS = − 0,077 − 0,0154 = − 0,0924.

Таким образом, в результате вышеприведенных действий получен вывод об устойчивости системы, определены запасы устойчивости и показатели качества, которые позволяют сделать общий вывод о правильности настройки системы. Для этого полученные показатели необходимо сравнить с некими требуемыми показателями устойчивости и качества.

Приведенная в примере система стабилизации угловой скорости турбогенератора является системой судовой автоматики, к которой предъявляются следующие требования:

- запас устойчивости по амплитуде: не менее 20 дБ;

- запас устойчивости по фазе: от 20 до 80°;

- перерегулирование: не более 10%;

- статическая ошибка: не более ±5% (±0,05).

Сравниваем полученные значения с требуемыми:

- запас устойчивости по амплитуде: менее 20 дБ и 2,37 дБ;

- запас устойчивости по фазе: от 20 до 80° и 9,75°;

- перерегулирование: 10% и 76,3%;

- статическая ошибка: 0,05 и −0,077 – не учитывая возмущающее воздействие и −0,0924, учитывая возмущающее воздействие.

Таким образом, анализируемая в примере система с указанными настройками регулятора работоспособна, но нуждается в дополнительной настройке, которая является задачей синтеза. Причем может оказаться, что с данным регулятором невозможно добиться указанных требований и придется изменить структуру регулятора.