Характеристического уравнения
Решение уравнения (5.1) представляет собой сумму слагаемых, вид которых определяется значениями корней характеристического уравнения. Если система представлена в виде передаточной функции, то для анализа устойчивости используется ее собственный оператор (знаменатель передаточной фикции).
Полученные корни характеристического уравнения могут быть представлены в виде точек на комплексной плоскости.
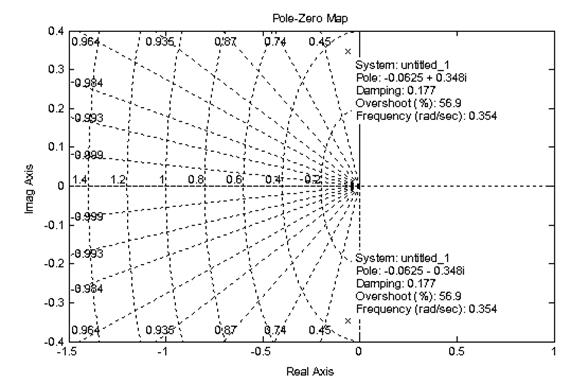
Рис.5.2. Определение устойчивости САУ по корням
характеристического уравнения
Для устойчивых систем необходимо и достаточно, чтобы все корни характеристического уравнения лежали слева от мнимой оси комплексной плоскости, то есть, как было сказано выше, были отрицательными. Если хотя бы один вещественный корень или пара комплексных сопряженных корней находится справа от мнимой оси, то система является неустойчивой. Если имеется нулевой корень или пара чисто мнимых корней, то система считается нейтральной (находящейся на границе устойчивости и неустойчивости). Таким образом, мнимая ось комплексной плоскости является границей устойчивости.
В пакете Simulink устойчивость системы по корням характеристического уравнения определяется с использованием пакета расширения LTI Viewer путем нажатия правой кнопки на поле графика и выбора пункта контекстного меню Plot Type > Pole/Zero (рис.5.2).
Для примера, изображенного на рис.5.2, система является устойчивой, так как имеет единственную пару сопряженных корней с отрицательной вещественной составляющей (лежат левее мнимой оси).
5.1.2. Частотный критерий устойчивости Найквиста
Частотный критерий устойчивости Найквиста позволяет оценить устойчивость замкнутой системы автоматического управления по амплитудно-фазовой или логарифмическим частотным характеристикам разомкнутой системы автоматического управления, если известно, что разомкнутая система является устойчивой.
При этом определение устойчивости системы автоматического управления по амплитудно-фазовой частотной характеристике существенно отличается от определения устойчивости по логарифмическим частотным характеристикам. Поэтому существуют два отдельных определения частотного критерия устойчивости Найквиста: для амплитудно-фазовой и логарифмической частотной характеристик.
Для амплитудно-фазовой частотной характеристики это определение звучит следующим образом: для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы, при изменении частоты от 0 до ¥, не охватывала точку с координатами (−1, j0).
Если АФЧХ разомкнутой системы проходитчерез точку с координатами (−1, j0), то система находится на границе устойчивости.
Для логарифмических частотных характеристик это определение имеет другой вид: для устойчивости замкнутой системы необходимо и достаточно, чтобы ЛАХ разомкнутой системы пересекла ось абсцисс раньше, чем ЛФХ, спадая окончательно, перешла за значение −p (−180°).
Точка, в которой ЛАХ пересекает ось абсцисс, называется частотой среза и обозначается wс.
Точка, в которой ЛФХ пересекает значение −p (−180°) спадая окончательно, называется частотой фазового сдвига и обозначается wp.
Для вышепринятых обозначений условия устойчивости по критерию Найквиста для ЛЧХ выглядят следующим образом:
1) если wс < wp, то система является устойчивой;
2) если wс > wp, то система является неустойчивой;
3) если wс = wp, то система находится на границе устойчивости.
В пакете Simulink для определения устойчивости системы с наличием обратной связи (замкнутой системы) по критерию Найквиста необходимо разомкнуть цепь обратной связи, то есть превратить систему в разомкнутую. Для этого нужно удалить одну из соединительных линий в цепи обратной связи и переставить точку выхода (для пакета LTI Viewer). На рис.5.3 в качестве примера приведена структурная схема замкнутой системы стабилизации угловой скорости турбогенератора, а на рис.5.4 – структурная схема этой же системы, но в разомкнутом виде.
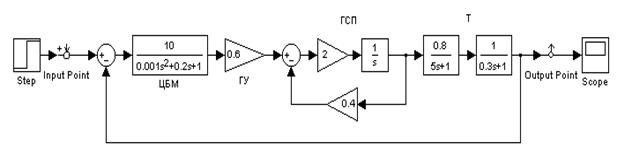
Рис.5.3. Пример замкнутой системы
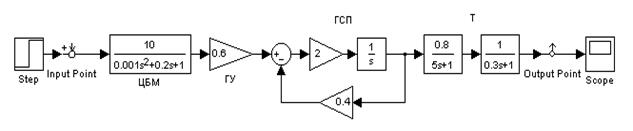
Рис.5.4. Пример разомкнутой системы
В пакете Simulink устойчивость системы по критерию Найквиста определяется с использованием пакета расширения LTI Viewer с помощью нажатия правой кнопки на поле графика и выбора из контекстного меню:
1) для АФЧХ: Plot Type > Nyquist (рис.5.5);
2) для ЛЧХ: Plot Type > Bode (рис.5.6).
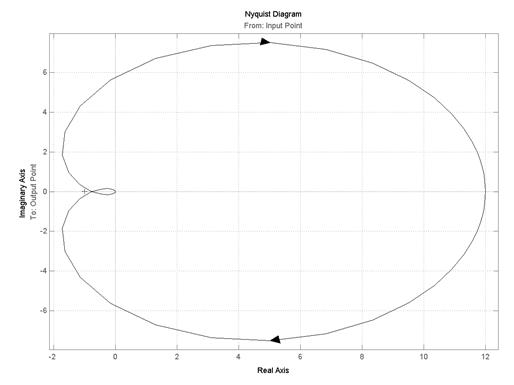
Рис.5.5. Определение устойчивости САУ по АФЧХ
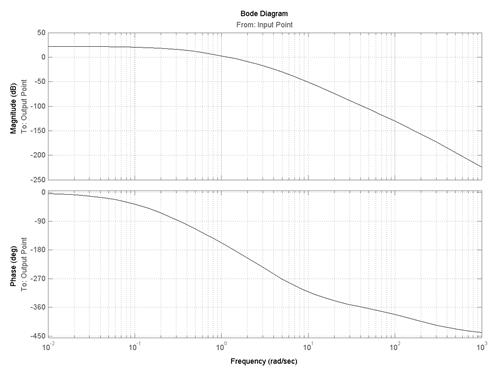
Рис.5.6. Определение устойчивости САУ по ЛЧХ
Из рис.5.5 видно, что АФЧХ разомкнутой системы не охватывает точку с координатами (−1, j0) (обозначена на графике красным крестиком), следовательно, замкнутая система стабилизации угловой скорости турбогенератора, структурная схема которой приведена на рис.5.3 и 5.4, является устойчивой. Такой же вывод можно сделать из анализа ЛЧХ (см. рис.5.6), так как ЛАХ пересекает ось абсцисс раньше, чем ЛФХ, окончательно спадая, переходит за значение −p (−180°). Для данной системы wc = 1,2 рад/с, а wp = 1,39 рад/с, то есть wc < wp и, следовательно, система устойчива.
5.2. Определение запасов устойчивости систем
автоматического управления
Вывод об устойчивости системы автоматического управления не является достаточным для определения устойчивости, поскольку существует вопрос: «Насколько устойчива система?». Для ответа на данный вопрос необходимо определить так называемые показатели запасов устойчивости.
В случае применения частотных критериев устойчивости Найквиста таких показателей два (рис.5.7):
1) запас устойчивости по амплитуде DL, измеряемый в децибелах (дБ) и показывающий, на сколько следует сдвинуть ЛАХ, чтобы система оказалась на границе устойчивости (см. рис.5.7, пунктирная линия);
2) запас устойчивости по фазе Dj, измеряемый в градусах и показывающий, на сколько следует сдвинуть ЛФХ, чтобы система оказалась на границе устойчивости (см. рис.5.7, пунктирная линия).
Запасы устойчивости получаются следующим образом (рис.5.7):
1) из точки пересечения ЛФХ, при окончательном ее спаде, c линией, проведенной на уровне −180° (частота фазового сдвига), поднимается перпендикуляр до пересечения с ЛАХ. Расстояние от этой точки до оси абсцисс даст искомое значение запаса устойчивости по амплитуде (DL, дБ);
2) из точки пересечения ЛАХ оси абсцисс (частота среза) опускается перпендикуляр до пересечения с ЛФХ, расстояние от этой точки до уровня −180° даст искомое значение запаса устойчивости по фазе (Dj, °).
В пакете Simulink численные значения запасов устойчивости системы автоматического управления можно определить по ЛЧХ или АФЧХ. Для получения ЛЧХ нужно в пакете LTI Viewer нажать правой кнопкой мыши на график и выбрать пункт меню Plot Type > Bode (см. рис.5.6).
Для определения запасов устойчивости необходимо щелкнуть правой кнопкой мыши на поле графика, и выбрать пункт контекстного меню Characteristics > Stability Margins (Min).
Для получения численных значений запасов устойчивости необходимо подвести курсор мыши к выделенным на графике точкам (рис.5.8 и 5.9) для системы, представленной на рис.5.4.
При этом в появляющихся окошках указаны численные значения запасов и частота в соответствующих точках логарифмических частотных характеристик:
 |
Рис.5.7. Определение запасов устойчивости
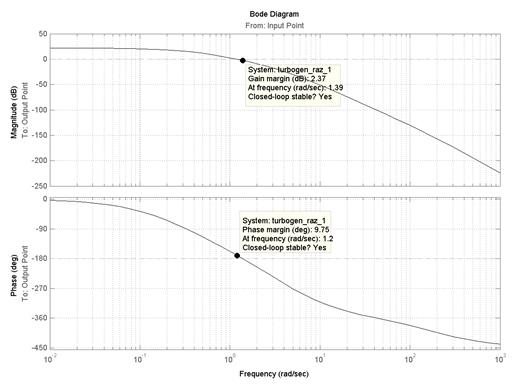
Рис.5.8. Определение запасов устойчивости по ЛЧХ
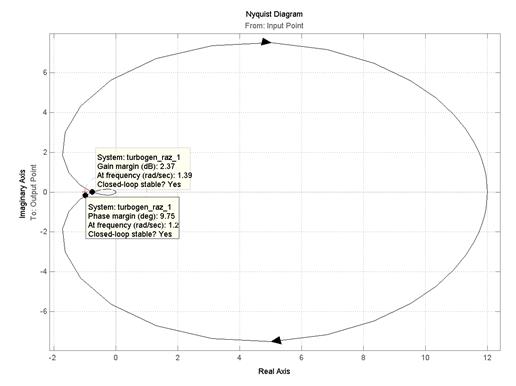
Рис.5.9. Определение запасов устойчивости по АФЧХ
· Gain margin (dB) – запас устойчивости по амплитуде, дБ;
· Phase margin (deg) – запас устойчивости по фазе, градусы;
· At frequency (rad/sec) – “на частоте”, рад/с.
Кроме того, делается вывод об устойчивости замкнутой системы Closed-loop stable? (Замкнутая система устойчива?), который может принимать два значения: Yes (Да) и No (Нет).
