Звено с постоянным запаздыванием

Для любого устройства, служащего для передачи информации, справедливо то, что выходная величина проявляется с некоторым запаздыванием на время t относительно момента поступления информации на вход устройства. В ряде случаев это время настолько мало, что им пренебрегают и считают, что практически информация на входе и выходе возникает в один и тот же момент.

Звено определяется как запаздывающее, если оно описывается уравнением

y(t) = x(t – t), (3.21)

где t - время запаздывания.

Передаточная функция звена запаздывания:

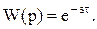(3.22)

Модель для исследования динамических свойств звена составляется из следующих блоков: Step, Transport Delay, Scope (рис. 3.25).

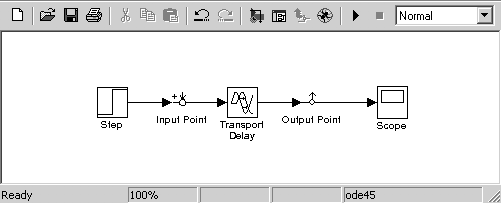
Рис.3.25. Модель звена с постоянным запаздыванием (t =1)

Для изменения параметров звена необходимо сделать двойной щелчок левой кнопкой мыши по элементу Transport Delay в окне модели. В открывшемся окне в поле Time delay (время запаздывания) вводим нужное значение.

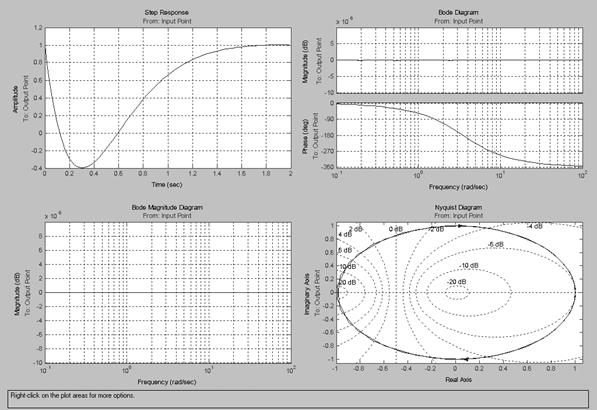
Рис.3.26. Переходные и частотные характеристики звена с постоянным

запаздыванием (t = 1, Pade Order = 2)

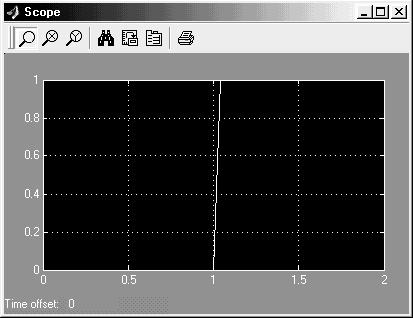
Рис.3.27. Переходный процесс звена с постоянным

запаздыванием, полученный с помощью блока Scope

Переходные и частотные характеристики звена с постоянным запаздыванием представлены на рис.3.26.

Из представленных характеристик видно, что данное звено не совсем точно отрабатывается в LTI Viewer – переходный процесс далек от идеального, но при просмотре переходного процесса при помощи блока Scope он выглядит близко к идеальному (рис.3.27). В версии MATLAB 6.5 для устранения этого недостатка в библиотеке Simulink Extras имеется дополнительная группа блоков Linearisation (рис. 3.28), один из которых – Switch transport delay for linearisation предназначен для использования в моделях с LTI Viewer.

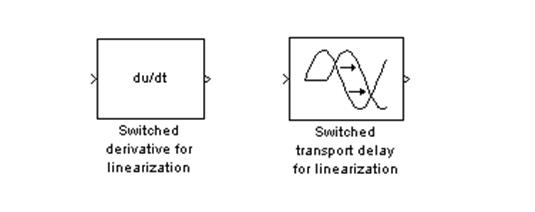
Рис. 3.28. Блоки Linearisation

Для увеличения точности данного звена необходимо изменять его настройку Pade Order (порядок функции-аппроксимации Паде), чем больше это число, тем ближе переходный процесс к идеалу и тем дольше ведется расчет. Наиболее оптимальным числом является Pade Order = 10.

Логарифмическая фазовая частотная характеристика не уходит в бесконечность и достоверна на протяжении 1,5 декады (до точки перегиба).

4. СПОСОБЫ СОЕДИНЕНИЯ ЗВЕНЬЕВ

В СТРУКТУРНУЮ СХЕМУ

Последовательное соединение звеньев

При последовательном соединении звеньев выходная величина предыдущего звена является входной величиной последующего. Результирующая передаточная функция последовательно соединенных звеньев равна произведению передаточных функций отдельных звеньев:

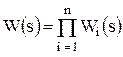. (4.1)

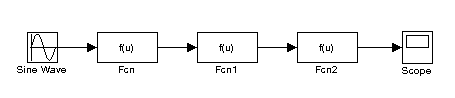
Рис.4.1. Последовательное соединение звеньев в пакете

Simulink

В пакете Simulink последовательное соединение получается простым соединением звеньев (рис.4.1).