Знакомство с программным продуктом matlab

ЗНАКОМСТВО С ПРОГРАММНЫМ ПРОДУКТОМ MATLAB

Основные сведения о системе MATLAB

Использование персональных компьютеров в учебном процессе позволяет облегчить труд преподавателя и дать практические навыки в решении тех или иных задач, возникающих в процессе обучения. Для этих целей используется целый набор интегрированных программных систем и пакетов программ, охватывающих практически весь спектр решаемых задач. В частности, средства для автоматизации математических расчетов: Reduce, Derive, TK Solver, Mathcad, Mathematica, Maple V, MATLAB и многие другие.

Система автоматизации математических расчетов MATLAB является одной из старейших и мощнейших в этой области. Название системы произошло от сокращения – МАТричная ЛАБоратория (MATrix LABoratory), но эта ориентация программы практически не ощущается теми пользователями, которые не интересуются непосредственно матричными вычислениями, вследствие проработанности и продуманности синтаксиса языка программирования системы.

Система MATLAB была разработана фирмой Math Works, Inc. как язык программирования высокого уровня для математических, инженерных, научных и технических вычислений. В процессе развития система “обрастала” различными дополнениями в виде пакетов расширения, с увеличением количества которых росли и возможности системы. Но также несколько увеличилась сложность ее освоения на первых этапах, что несколько компенсируется развитой системой помощи (на английском языке).

Как и всякая компьютерная программа, система MATLAB обладает как достоинствами, так и недостатками. Достоинства системы очевидны и частично описаны выше, лишь необходимо отметить легкость написания программ в данной системе и открытость ее архитектуры, что позволяет легко изменять систему “под себя” и создавать новые пакеты расширений. К недостаткам системы можно отнести: линейную запись выражений и формул, что по сравнению, например, с системой Mathcad выглядит несколько неудобочитаемым; некоторую громоздкость системы, что создает сложности в ее изучении на первых этапах.

В данный момент существует довольно большое количество литературы, посвященной системе MATLAB и ее приложениям, но даже вся эта литература не может охватить все возможности и способности этого программного продукта. В частности, недостаточно освещен вопрос о применении системы MATLAB (а точнее, пакета расширения Simulink) для решения задач анализа и синтеза систем автоматического управления (САУ). Поскольку данное учебное пособие посвящено исключительно этому вопросу, в нем будет использоваться только пакет расширения Simulink и работа непосредственно с системой MATLAB описываться не будет. Но так как пакет расширения Simulink не может функционировать без системы MATLAB, в следующем подразделе даны краткие рекомендации по пользованию системой MATLAB.

Также необходимо отметить, что данное учебное пособие ориентировано на использование версии MATLAB 6.0 Release 12 и версии Simulink 4.0 (далее в тексте - без номера версии).

Вопросы установки системы MATLAB также опускаются.

Предполагается, что MATLAB используется в операционной системе Windows 95 OSR2, Windows 98 или Windows 98 OSR2. Запуск системы MATLAB 6.0 производится из главного меню операционной системы либо двойным щелчком левой кнопки мыши на иконке MATLAB на рабочем столе.

После запуска появляется основное окно системы MATLAB. Это обычное окно приложений Windows, его можно перемещать, изменять его размер, открывать на весь экран и т. д.

Рабочего пространства

Панель запуска (рис.1.5) предназначена для быстрого доступа к компонентам системы MATLAB (в том числе и к Simulink) и к их описаниям, а также к ссылкам Internet.

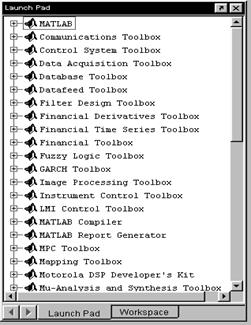
Рис.1.5. Панель запуска компонентов

системы MATLAB

Браузер рабочего пространства (рис.1.6) предназначен для удобного просмотра хранящихся в оперативной памяти переменных, используемых системой при своей работе (пакет расширения Simulink также создает переменные в рабочей области).

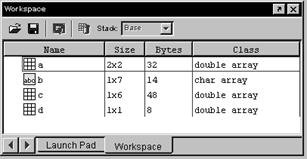
Рис.1.6. Браузер рабочего пространства

системы MATLAB

1.2.4. Окно истории сессии и браузер текущей директории

В окне истории сессии (рис.1.7) отображаются все команды, выполненные при предыдущих запусках системы, которые хранятся до перезагрузки компьютера. При необходимости сессию можно сохранить.

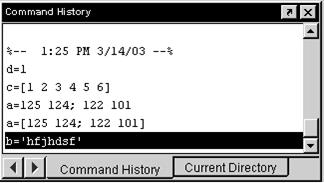
Рис.1.7. Окно истории сессии системы MATLAB

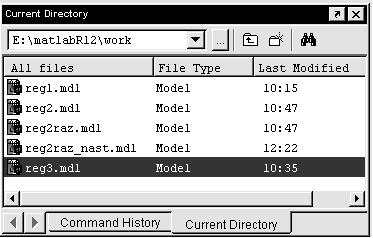
Рис.1.8. Браузер текущей директории системы MATLAB

Браузер текущей директории (рис.1.8) отображает содержимое текущей директории (рабочего каталога) системы (см. рис.1.4, поз.10), а также указывает тип файла и время его последнего изменения.

2. ПАКЕТ МОДЕЛИРОВАНИЯ ДИНАМИЧЕСКИХ

СИСТЕМ SIMULINK

Блоки библиотеки Simulink

2.2.1. Continuous – раздел непрерывных блоков

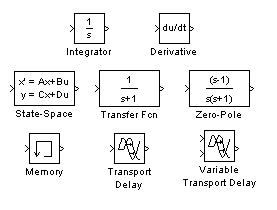
Рис. 2.3. Раздел Continuous

В состав раздела непрерывных блоков входят (рис 2.3):

· Derivative – дифференцирующий блок;

· Integrator – интегрирующий блок;

· Transport Delay – блок постоянного запаздывания;

· Transfer Fcn – блок, реализующий передаточную функцию, заданную в виде отношения полиномов (апериодическое и колебательное звенья);

· State-Space – линейная аналоговая система, заданная в виде уравнений состояния, т. е. в виде системы уравнений, представленной в форме Коши;

· Zero-Pole – линейная аналоговая система, заданная своими нулями и полюсами;

· Memore – блок памяти, выполняющий задержку на один шаг модельного времени;

· Variable Transport Delay – блок памяти с переменной задержкой.

2.2.2. Discrete – раздел дискретных блоков

· Discrete Transfer Fcn - блок, реализующий передаточную функцию, заданную в виде отношения полиномов (апериодическое и колебательное звенья), для дискретных САУ;

· Discrete Time Integrator – интегрирующий блок для дискретных САУ. Выполняет численное интегрирование входного сигнала;

· Zero-Order-Hold –экстраполятор нулевого порядка;

· Unit Delay – блок задержки сигнала. Обеспечивает задержку входного сигнала на заданное число шагов модельного времени;

· Discrete State-Spase – блок задания дискретного звена матрицами его состояния;

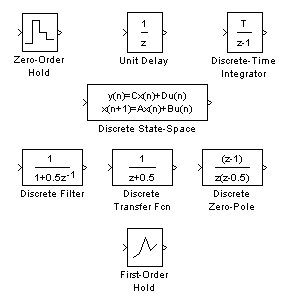
Рис. 2.4. Раздел Discrete

· Discrete Filter – блок задания дискретного звена через дискретную передаточную дробно-рациональную функцию относительно 1/Z;

· Discrete Zero-Pole – блок задания дискретного звена через указание значений нулей и полюсов дискретной передаточной функции относительно 1/Z;

· First-Order Hold – экстраполятор первого порядка.

2.2.3. Function & Tables – раздел блоков функций и таблиц

· Fcn – блок, реализующий в пакете Simulink любую функцию системы MATLAB, где в качестве параметра настройки можно ввести любое вычисляемое выражение, аргументом которого выступает входной сигнал;

· MATLAB Fcn – подобен предыдущему блоку, но также позволяет реализовывать m-функции (программы, написанные на языке программирования MATLAB);

· Look-Up Table, (2-D) и (n-D) – блоки данных, заданных в виде таблиц (позволяют задать нелинейные блоки любого вида), отличаются друг от друга размерностью задающих таблиц. Все эти блоки выполняют различного вида интерполяции.

2.2.4. Math – раздел математических блоков

· Gain – усилительный блок;

· Sum – сумматор сигналов с различными знаками и любым количеством входов;

· Product – вычислитель, формирующий на выходе результат умножения или деления двух и более входных сигналов. В качестве параметров настройки указывается число входов и вид выполняемой операции;

· Dot Product – звено, осуществляющее перемножение двух входных величин, если они являются скалярами. Это звено вычисляет также сумму поэлементных произведений двух входных векторов одинаковой длины;

· Slider Gain – аналоговый усилитель с интерактивной настройкой;

· Matrix Gain – усилитель, на вход которого подается вектор;

· Mat Function – блок, позволяющий выбрать одну из математических функций в поле настройки и включить ее в модель;

· Trigonometric Function – звено формирования тригонометрических функций от входного сигнала. Выбор функции обеспечивается в поле настройки;

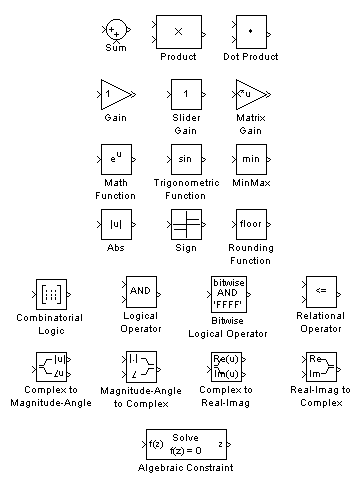
Рис. 2.5. Раздел Math

· MinMax – блок выбирает минимальное или максимальное значение вектора в соответствии с заданием поля настройки. Входной сигнал на блок задается числовым вектором. В окне настройки определяется также количество входов;

· Abs – блок, формирующий на выходе абсолютное значение входного сигнала;

· Sign – блок-реле, реагирующий на знак входного сигнала;

· Rounding Function – округление входного сигнала;

· Combinatorial Logic – блок обеспечивает преобразование входного сигнала в соответствии с формированной в окне настройки таблицей истинности;

· Logical Operation и Relaition Operator – блоки производят известные логические операции «и» и «или», количество входов задается в поле настройки;

· Bitwise Logical Operator – универсальный блок, реализующий любую логическую функцию;

· Complex to Magnitude-Angle – блок, позволяющий выделить модуль и фазу входной комплексной величины;

· Magnitude-Angle to Complex – блок, преобразующий входную величину, заданную модулем и фазой в комплексную выходную величину;

· Complex to Real-Image, Real-Image to Complex – блоки, преобразующие комплексные величины из показательной формы в алгебраическую и обратно;

· Algebraic Constrain – блок, позволяющий в структурную модель включать систему алгебраических уравнений.

2.2.5. Nonlinear – раздел нелинейных блоков

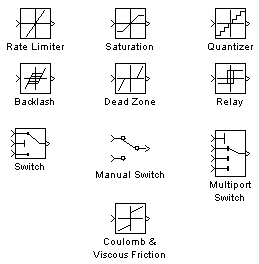
Рис. 2.6. Раздел Nonlinear

· Saturation – блок ограничения;

· Dead Zone – блок с зоной нечувствительности;

· Relay – релейный блок;

· Rate Limiter – блок с ограничением скорости;

· Coulomb and Viscous Friction – блок фрикционных эффектов;

· Backlash – блок люфта;

· Switch и Multiport Switch – переключатели одно- и многовходовые;

· Quantizer – блок, обеспечивающий квантование входного сигнала по уровню. В системах управления такие блоки являются частью аналого-цифрового преобразователя;

· Manual Switch – блок, который переключается вручную. В процессе моделирования при помощи этого ключа удобно менять параметры и структуру модели;

· Coulumb & Viscous Friction – блок, реализующий характеристику трения в механических системах.

2.2.6. Signal & Systems – раздел блоков сигналов и систем

· Sub System – блок-подсистема (полезен в случае громоздких систем, части которых можно с помощью данного блока заменить на один или несколько блоков-подсистем);

· In, Out – блоки входа/выхода, предназначенные для создания блоков-подсистем;

· Mux – микшер сигналов, собирающий несколько сигналов в одну шину;

· Demux – блок, выполняющий действие, обратное действию предыдущего блока;

· Enable, Trigger – блоки, предназначенные для логического управления работой модели;

· Bus Selector – блок выделяет из присоединенной к его порту шины требуемые сигналы. В окне настройки блока имеется два списка – входной и выходной;

· Selector – блок выбирает из входного вектора элементы, которые указаны в параметрах настройки;

· Merge – блок, осуществляющий объединение входных сигналов;

· Matrix Concatenation – блок, позволяющий векторный сигнал, представленный развернутой строкой или столбцом, преобразовать к «свернутому» векторному сигналу;

· From, Goto Tag Visibility, Goto – блоки ( «Принять», «Признак видимости», «Передать» ) используются совместно и предназначены для обмена между различными данными модели с учетом их доступности;

· Data Store Memory, Data Store Read, Data Store Write – «Память», «Чтение» и «Запись» данных, также используются совместно и обеспечивают хранение и передачу данных;

· Ground, Terminator – блоки используются в качестве «заглушек» для неиспользованных входных и выходных портов соответственно;

Рис. 2.7. Раздел Signal & Systems

· Reshape – блок, позволяющий изменить размерность входного сигнала;

· Data Type Conversion – блок, обеспечивающий приведение типа данных входного сигнала к требуемому;

· Function-Call Generator – блок, обеспечивающий запуск подключенных к нему подсистем с заданной периодичностью;

· Configurable Subsystem – блок, реализующий функцию любой подсистемы, которая может быть библиотечной или созданной пользователем;

· Model info – блок, позволяющий получить информацию о модели;

· IC – блок, позволяющий установить начальное значение входного сигнала, значение которого задается в окне настройки;

· Width – блок, вычисляющий размерность сигнала на входе;

· Probe – блок, позволяющий получить на выходе необходимую информацию о входном сигнале. Блок имеет один вход, число выходов зависит от числа исследуемых параметров входного сигнала;

· Signal Specification – блок, управляющий процессом моделирования в зависимости от параметров входного сигнала.

2.2.7. Sinks – раздел блоков получателей сигналов

· Display – блок, отображающий цифровую информацию (уровень сигнала в данный момент времени);

· Scope – виртуальный осциллограф, предназначенный для получения временных зависимостей (переходных процессов);

· XY Graph – виртуальный графопостроитель (построение фазовых портретов и различных двухмерных графиков);

Рис. 2.8. Раздел Sinks

· To File и To Workspace – блоки, передающие информацию в файл или в рабочую область MATLAB;

· Stop Simulink – остановка симуляции.

2.2.8. Sources – раздел блоков источников сигналов

· Band-Limited White Noice – генератор белого шума;

· Chrip Signal – генератор сигнала с нарастающей частотой;

· Constant - источник постоянного воздействия, задающий константу (t < 0, y = 0; t ³ 0, y = сonst);

· Discrete Pulse Generator – источник дискретных импульсов;

· From File и From Workspace - источником сигнала для этих блоков служит файл или рабочая область MATLAB;

· Ramp – источник нарастающего воздействия;

Рис. 2.9. Раздел Sources

· Random Number – источник случайного сигнала с нормальным распределением;

· Repeating Sequence – источник пилообразного сигнала;

· Sine Wave – источник синусоидального воздействия;

· Step – источник перепада сигнала (t < Step time, y = Initial value; t > Step time, y = Final value);

· Signal Generator – универсальный сигнал-генератор;

· Clock – источник времени моделирования;

· Digital Clock – цифровой источник времени.

2.2.9. Библиотека Simulink Extras

Библиотека Simulink Extras является дополнительной библиотекой пакета Simulink. Эта библиотека содержит наборы блоков с более широкими функциями, чем рассмотренные ранее разделы основной библиотеки. Тем не менее это вовсе не означает, что применение этой библиотеки всегда предпочтительнее. Связано это с тем, что усложнение функций блоков, полезное при решении ряда специфических задач, оборачивается усложнением моделирования при решении большинства обычных задач.

Библиотека Simulink Extras представлена на рис. 2.10. Работа с этой библиотекой ничем не отличается от работы с основной библиотекой.

Рис.2.10. Библиотека Simulink Extras

2.2.9.1.Additional Discrete – дополнительные дискретные блоки

Рис. 2.11. Дополнительные

дискретные блоки

Дополнительные блоки Additional Discrete представлены всего четырьмя блоками – по два варианта известных нам блоков Discrete Transfer Fcn и Discrete Zero-Pole (рис 2.11). Их единственным отличием от описанных ранее блоков является возможность инициализации входов и состояний.

2.2.9.2.Additional Linear – дополнительные линейные блоки

Состав дополнительных линейных блоков раздела Additional Linear показан на рис. 2.12. Блоки этого раздела можно разделить на две категории: PID-контроллеры и блоки типа State-Shfct, Transfer Fnc и Zero-Pole, дополненные возможностями выходных сигналов и состояний.

Для анализа и синтеза систем управления наибольший интерес представляют PID-контроллеры. Первый из них PID-controller – это довольно универсальный блок, выходной сигнал которого задается операторным выражением:

OUT = P + I / s + Ds,

где Р – входной сигнал; I – его интеграл; D – его производная.

Рис. 2.12. Дополнительные линейные

блоки

Параметр Р (по умолчанию 1) фактически задает коэффициент усиления безынерционного усилительного звена. Параметр I задает пропорциональность интегралу входного сигнала и, наконец, параметр D задает пропорциональность производной входного сигнала. Параметры P, I и D задаются в таблице настройки PID-контроллера, поэтому задавая различные значения указанных параметров, можно получить П -, ПИ -, ПД - и ПИД - регуляторы .

Второй PID-controller (with Approximate Derivative) c улучшенной операцией дифференцирования вычисляет выходной сигнал как:

OUT = Р + I / s + Ds/(1/Ns + 1).

За счет применения дополнительного параметра N улучшается вычисление производной.

2.2.9.3.Дополнительные блоки Additional Sinks

Раздел дополнительных блоков Additional Sinks содержит ряд новых виртуальных регистраторов ( рис. 2.13):

· Auto Correlator – автокоррелятор (используется с пакетом Signal Processing Toolbox);

· Averaging Power Spectral Density – анализатор спектральной плотности мощности с усреднением;

Рис. 2.13. Дополнительные блоки

Additional Sinks

· Averaging Spectrum Analyzer – спектральный анализатор с усреднением;

· Cross-Correlator – кросс-коррелятор;

· Floating Point Bar – утилита построения гистограммы;

· Power Spectral Density – анализатор спектральной плотности мощности;

· Spectrum Analyser – анализатор спектра.

Данные блоки относятся к двум важным разделам моделирования – статистическому анализу и анализу спектров сигналов ( по уровню и по мощности ).

2.2.9.4.Блоки триггеров Flip Flops

Рис. 2.14. Раздел библиотеки Flip Flops

Раздел библиотеки Simulink Extras Flip Flops содержит следующие основные блоки (рис. 2.14):

· Clock – генератор тактовых импульсов;

· D Flip Flops, D Latch, J-K Flip Flops, R-S Flip Flops – 4 триггерных устройства типа D -, J-K, R-S – триггеров.

2.2.9.5.Раздел преобразований Transformations

Раздел преобразований Transformations (рис. 2.15) содержит 8 блоков для осуществления типичных преобразований – температуры из градусов Цельсия в градусы Фаренгейта и наоборот; углов, выраженных в градусах, в углы, выраженные в радианах, и наоборот; прямоугольных систем координат в полярные системы координат и наоборот.

Рис. 2.15. Блок Transformations

Основные настройки вышеописанных блоков и правила работы с ними описаны ниже.

Любая модель, собираемая в программном пакете Simulink, должна состоять из трех основных частей: источник сигнала, модель, приемник сигнала. Причем модель может состоять из любых блоков, описанных выше (кроме разделов источников и приемников сигналов).

Колебательное звено

Колебательным называют звено, у которого при ступенчатом изменении входной величины выходная величина стремится к новому установившемуся значению, совершая при этом колебания.

Уравнение колебательного звена в операторной форме записи:

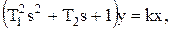(3.11)

где T₁ и T₂ – постоянные времени колебательного звена; k – коэффициент усиления колебательного звена.

Передаточная функция колебательного звена:

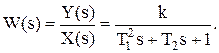(3.12)

Постоянные времени колебательного звена T₁ и T₂ связаны зависимостью

x = Т₂ / 2Т₁. (3.13)

Коэффициент x называют коэффициентом колебательности и, судя по названию, он характеризует колебательность переходного процесса колебательного звена.

Если x < 1, то переходный процесс звена – колебательный, и чем x меньше единицы, тем колебательнее процесс.

Если x ³ 1, то получаем апериодическое звено второго порядка.

Модель для исследования динамических свойств звена состоит из следующих блоков: Step, Transfer Fcn, Scope.

Полученная модель показана на рис.3.19.

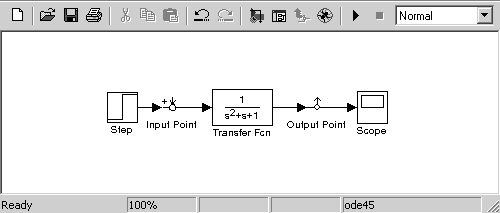
Рис.3.19. Модель колебательного звена (k = 1, T₁² = 1, T₂ = 1)

Методика изменения коэффициентов звена Transfer Fcn приведена в п.3.5 для апериодического звена, единственное отличие – для колебатель -

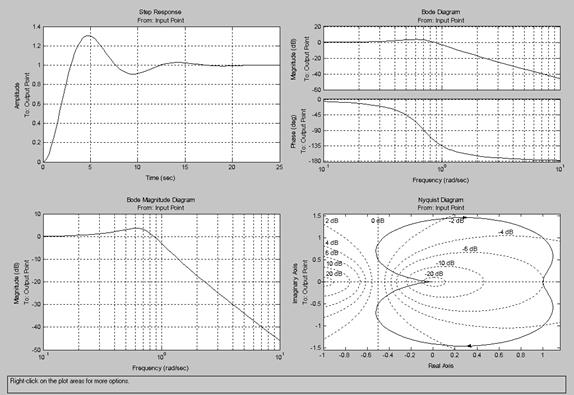
Рис.3.20. Переходные и частотные характеристики колебательного

звена (k = 1, T₁² = 1, T₂ =1)

ного звена в окне Denominator вводим [T₁² T₂ 1] (также через пробел), поскольку в знаменателе колебательного звена находится полином вида
a₀s² + a₁s¹ + a₂s⁰, где a₀ = T₁², а₁ = T₁, a₂ = 1.

Переходные и частотные характеристики колебательного звена представлены на рис.3.20.

Интегрирующее звено

Интегрирующим называют звено, в котором выходная величина пропорциональна интегралу во времени от входной величины.

Уравнение интегрирующего звена:

sy = kx, (3.14)

где k – коэффициент усиления интегрирующего звена.

В интегральной форме:

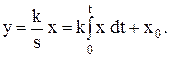(3.15)

При ступенчатом входном сигнале выходная величина линейно зависит от времени:

у = kxt = Kt, (3.16)

где K = kx - постоянная величина; t - время.

В интегрирующем звене скорость изменения выходной величины пропорциональна входной величине.

Уравнение звена в операторной форме:

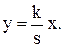(3.17)

Передаточная функция интегрирующего звена:

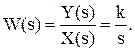(3.18)

Рис.3.21. Модель интегрирующего звена (k = 1)

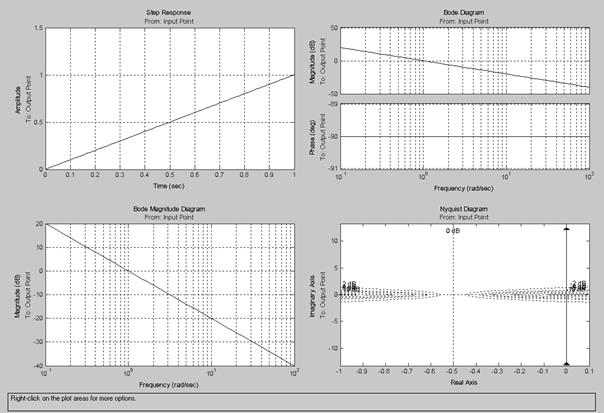
Рис.3.22. Переходные и частотные характеристики интегрирующего звена (k=1)

Модель для исследования динамических свойств звена состоит из следующих блоков: Step, Gain, Integrator, Scope. В связи с тем, что передаточная функция интегрирующего звена в пакете Simulink всегда 1/s, то для то-

го, чтобы задать коэффициент усиления интегрирующего звена, используется последовательное соединение усилительного (Gain) и интегрирующего звеньев (Integrator).

Полученная модель показана на рис. 3.21.

Учитывая все вышесказанное, для изменения коэффициента усиления интегрирующего звена необходимо изменять коэффициент передачи последовательно соединенного с ним усилительного звена (Gain). Параметры интегрирующего звена (Integrator) изменять не рекомендуется.

Переходные и частотные характеристики интегрирующего звена представлены на рис.3.22.

Дифференцирующее звено

Дифференцирующим называют звено, в котором выходная величина пропорциональна производной по времени от входной величины. В дифференцирующем звене выходная величина пропорциональна скорости изменения входной величины.

Уравнение идеального дифференцирующего звена в операторной форме записи:

у = ksx. (3.19)

При подаче на вход звена ступенчатого сигнала на выходе получается мгновенный выходной импульс, теоретически имеющий бесконечно большую амплитуду, соответствующую бесконечно большой скорости входного сигнала в момент подачи.

Передаточная функция идеального дифференцирующего звена:

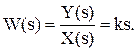(3.20)

Модель для исследования динамических свойств звена состоит из следующих блоков: Step, Gain, Switched derivative for linearization (из раздела Linearization библиотеки Simulink Extras), Scope. Здесь используется звено Switched derivative for linearization (из раздела Linearization библиотеки Simulink Extras), а не звено Derivative из раздела Continuous, поскольку последнее не оказывает нужного влияния на частотные характеристики системы.

В связи с тем, что передаточная функция дифференцирующего звена в пакете Simulink всегда s, то для того чтобы задать коэффициент усиления интегрирующего звена, используется последовательное соединение усилительного (Gain) и дифференцирующего звеньев (Switched derivative for linearization). Полученная модель показана на рис. 3.23.

Рис.3.23. Модель дифференцирующего звена (k =1)

Учитывая вышесказанное, для изменения коэффициента усиления дифференцирующего звена необходимо изменять коэффициент передачи, последовательно соединенного с ним усилительного звена (Gain). В параметрах блока Switched derivative for linearization устанавливаем: Switch value = 1 и Derivative constant = 10⁷ (чем больше последнее значение, тем точнее звено, но дольше время моделирования).

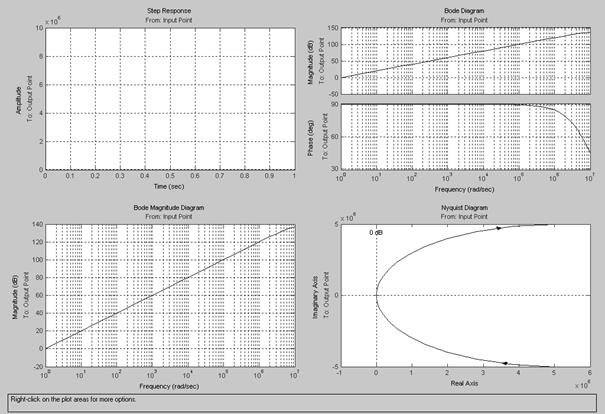
Рис.3.24. Переходные и частотные характеристики дифференцирующего звена (k=1)

Причем логарифмические характеристики для данного звена можно считать достоверными на интервале от 10⁰ до частоты, на два порядка меньшей, чем значение Derivative constant, заданное в окне параметров блока Switched derivative for linearization (рекомендуем установить это значение, равным 10⁷, тогда график достоверен на интервале до 10⁵).

Характеристики звена представлены на рис. 3.24.

Автоматического управления

Устойчивость – это свойство системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия.

Это понятие хорошо описывается тремя простыми примерами (рис.5.1):

1. Шар, находящийся на вершине горки (рис.5.1, а), является примером неустойчивой системы, так как при приложении к нему конечного возмущения (сторонней силы) он скатится с горки и в исходное положение не вернется.

2. Шар, находящийся во впадине, является примером устойчивой системы, так как при приложении к нему конечного возмущения он вернется в исходное положение (рис.5.1, б).

3. Шар, находящийся на плоскости, является примером системы, находящейся на границе устойчивости, так как при приложении к нему конечного возмущения он остановится, но уже в другом положении (рис.5.1, в).

Рис.5.1. Пример, иллюстрирующий понятие устойчивости

Таким образом, если система неустойчива, то достаточно любого толчка, чтобы в ней начался расходящийся процесс ухода из исходного установившегося состояния. А если система устойчива, то переходный процесс в системе, вызванный каким-либо воздействием, со временем затухает, и система вновь возвращается в устойчивое состояние.

Вышеприведенное понятие устойчивости определяет устойчивость установившегося режима системы, тогда как система может работать в условиях непрерывно изменяющихся воздействий, когда установившийся режим вообще отсутствует. Тогда с учетом таких условий работы можно дать следующее, более общее определение устойчивости: система устойчива, если ее выходная величина остается ограниченной в условиях действия на систему ограниченных по величине возмущений.

Устойчивость является основной оценкой динамических свойств систем автоматического управления. Устойчивость систем автоматического управления связана с характером её поведения после прекращения внешнего воздействия. Это поведение описывается свободной составляющей решения дифференциального уравнения, которое описывает систему. Если свободная составляющая рабочего параметра объекта управления после прекращения внешнего воздействия стремится к нулю, то такая система является устойчивой. Другими словами, устойчивость системы − это есть затухание ее переходных процессов.

Если свободная составляющая стремится к конечному значению или имеет вид гармонических колебаний с постоянной амплитудой, то система считается нейтральной. В том случае, если свободная составляющая неограниченно возрастает или имеет вид гармонических колебаний с возрастающей амплитудой, то система считается неустойчивой.

Оценка устойчивости производится на основе результатов исследования свободной составляющей, которая представляет собой решение однородного дифференциального уравнения (которое называется характеристическим) при заданных начальных условиях:

(a₀sⁿ+a₁s^n-1+...+a_n-1)y=0. (5.1)

При этом система автоматического управления будет устойчива, если переходный процесс, вызванный любым возмущением, будет затухающим, то есть с течением времени будет стремиться к какому-то определенному значению. Для выполнения этого условия необходимо, чтобы действительная часть сопряженных корней характеристического уравнения системы была отрицательной.

В общем случае это требует составления передаточной функции замкнутой системы и получения корней характеристического уравнения, что достаточно сложно и трудоемко для сложных систем выше 3-го порядка.

Поэтому с целью упрощения анализа устойчивости систем разработан ряд специальных методов, которые получили название критериев устойчи­вости.

Критерии устойчивости делятся на две разновидности: алгебраические и частотные. Алгебраические критерии являются аналитическими, а частотные – графоаналитическими. Критерии устойчивости позволяют также оценить влияние параметров системы на устойчивость в виде запасов устойчивости.

В пакете Simulink возможно автоматическое применение трех критериев устойчивости:

1) по корням характеристического уравнения системы;

2) частотные критерии устойчивости Найквиста;

3) критерий устойчивости Никольса.

В нашей стране применяются в основном первые два.

5.1.1. Критерий устойчивости по корням

Рис.5.3. Пример замкнутой системы

Рис.5.4. Пример разомкнутой системы

В пакете Simulink устойчивость системы по критерию Найквиста определяется с использованием пакета расширения LTI Viewer с помощью нажатия правой кнопки на поле графика и выбора из контекстного меню:

1) для АФЧХ: Plot Type > Nyquist (рис.5.5);

2) для ЛЧХ: Plot Type > Bode (рис.5.6).

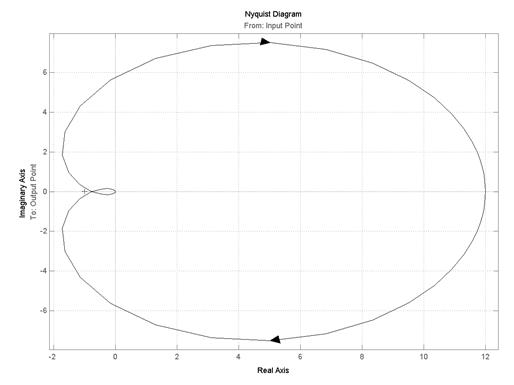
Рис.5.5. Определение устойчивости САУ по АФЧХ

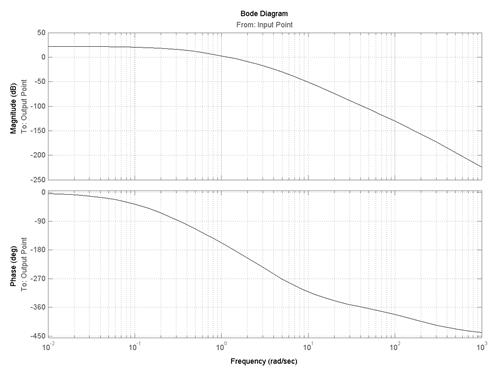
Рис.5.6. Определение устойчивости САУ по ЛЧХ

Из рис.5.5 видно, что АФЧХ разомкнутой системы не охватывает точку с координатами (−1, j0) (обозначена на графике красным крестиком), следовательно, замкнутая система стабилизации угловой скорости турбогенератора, структурная схема которой приведена на рис.5.3 и 5.4, является устойчивой. Такой же вывод можно сделать из анализа ЛЧХ (см. рис.5.6), так как ЛАХ пересекает ось абсцисс раньше, чем ЛФХ, окончательно спадая, переходит за значение −p (−180°). Для данной системы w_c = 1,2 рад/с, а w_p = 1,39 рад/с, то есть w_c < w_p и, следовательно, система устойчива.

5.2. Определение запасов устойчивости систем

автоматического управления

Вывод об устойчивости системы автоматического управления не является достаточным для определения устойчивости, поскольку существует вопрос: «Насколько устойчива система?». Для ответа на данный вопрос необходимо определить так называемые показатели запасов устойчивости.

В случае применения частотных критериев устойчивости Найквиста таких показателей два (рис.5.7):

1) запас устойчивости по амплитуде DL, измеряемый в децибелах (дБ) и показывающий, на сколько следует сдвинуть ЛАХ, чтобы система оказалась на границе устойчивости (см. рис.5.7, пунктирная линия);

2) запас устойчивости по фазе Dj, измеряемый в градусах и показывающий, на сколько следует сдвинуть ЛФХ, чтобы система оказалась на границе устойчивости (см. рис.5.7, пунктирная линия).

Запасы устойчивости получаются следующим образом (рис.5.7):

1) из точки пересечения ЛФХ, при окончательном ее спаде, c линией, проведенной на уровне −180° (частота фазового сдвига), поднимается перпендикуляр до пересечения с ЛАХ. Расстояние от этой точки до оси абсцисс даст искомое значение запаса устойчивости по амплитуде (DL, дБ);

2) из точки пересечения ЛАХ оси абсцисс (частота среза) опускается перпендикуляр до пересечения с ЛФХ, расстояние от этой точки до уровня −180° даст искомое значение запаса устойчивости по фазе (Dj, °).

В пакете Simulink численные значения запасов устойчивости системы автоматического управления можно определить по ЛЧХ или АФЧХ. Для получения ЛЧХ нужно в пакете LTI Viewer нажать правой кнопкой мыши на график и выбрать пункт меню Plot Type > Bode (см. рис.5.6).

Для определения запасов устойчивости необходимо щелкнуть правой кнопкой мыши на поле графика, и выбрать пункт контекстного меню Characteristics > Stability Margins (Min).

Для получения численных значений запасов устойчивости необходимо подвести курсор мыши к выделенным на графике точкам (рис.5.8 и 5.9) для системы, представленной на рис.5.4.

При этом в появляющихся окошках указаны численные значения запасов и частота в соответствующих точках логарифмических частотных характеристик:

Рис.5.7. Определение запасов устойчивости

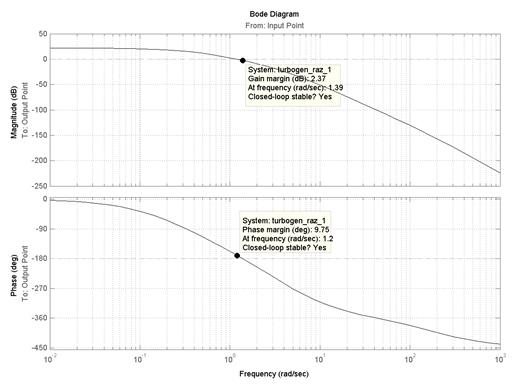
Рис.5.8. Определение запасов устойчивости по ЛЧХ

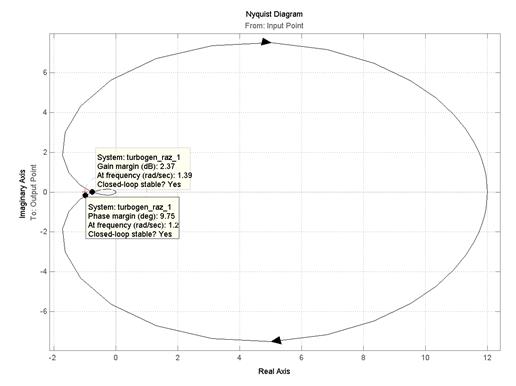
Рис.5.9. Определение запасов устойчивости по АФЧХ

· Gain margin (dB) – запас устойчивости по амплитуде, дБ;

· Phase margin (deg) – запас устойчивости по фазе, градусы;

· At frequency (rad/sec) – “на частоте”, рад/с.

Кроме того, делается вывод об устойчивости замкнутой системы Closed-loop stable? (Замкнутая система устойчива?), который может принимать два значения: Yes (Да) и No (Нет).

Автоматического управления

Для проведения анализа произвольной системы автоматического управления необходимо выполнить следующие действия (в качестве примера далее приводится анализ системы стабилизации угловой скорости турбогенератора).

1. Построить принципиальную или кинематическую схему САУ (рис.5.15) и выделить на ней отдельные функциональные элементы.

В схему входят следующие элементы: Т – турбина (объект управления); МП – механическая передача; ЦБМ – центробежный маятник (выполняет функции датчика, определяющего действительную угловую скорость, задатчика угловой скорости и сумматора, вычисляющего ошибку регулирования); ГУ – гидроусилитель; ГСП – гидравлический сервопривод; ПВК – паровпускной клапан с регулируемым расходом; Г – генератор, приводимый во вращение турбиной.

Некоторой установившейся нагрузке генератора соответствует определенная угловая скорость турбины, положение грузов ЦБМ и поршня ГСП, а также величина открытия ПВК. Если нагрузка уменьшится, угловая скорость турбины возрастет, грузы ЦМБ, а вместе с ними и муфта переместятся вверх (z). Переместится и золотник ГУ (s₁), поршень ГСП пока остается неподвижным (s₂ = 0), так как закрыты окна ГУ. Он приоткроет дос-

Рис.5.15. Принципиальная схема системы стабилизации угловой

Скорости турбогенератора

туп рабочего тела (жидкости) в верхнюю полость ГСП, поршень которого начнет перемещаться вниз и прикроет ПВК, который, в свою очередь, уменьшит подачу пара в турбину, вследствие чего у