Нестационарные процессы теплопроводности

11.2.1 Общие положения нестационарных процессов теплопроводности

При нагревании тела тепло, воспринимаемое его внешней поверхностью от окружающего пространства (печи), постепенно проникает внутрь материала вследствие его теплопроводности и разности температур поверхности и внутренних слоев материала.

Если температурное поле меняется во времени, то тепловые процессы, протекающие в таких условиях, называют нестационарными.

Нестационарные процессы теплопроводности встречаются при охлаждении металлических заготовок, работе регенеративных теплообменных аппаратов, прокаливании твердых тел, в производстве стекла, обжиге кирпича, вулканизации резины.

В качестве иллюстрации на рис. 11.5 изображен процесс нагревания однородного твердого тела в среде с температурой 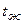. Здесь 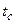- температура на поверхности тела, а 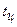- температура в центре тела. Из рис. 6 следует, что по истечении некоторого времени температура всех частей тела выравнивается и принимает значение, равное .

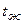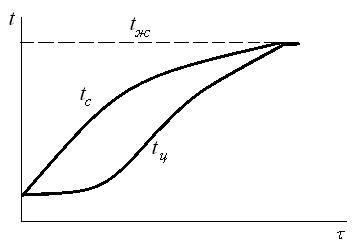
Рисунок 11.5 – Процесс нагревания однородного твердого тела

Рисунок 11.6 дает представление об изменении во времени теплового потока 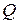, расходуемого на нагревание тела. В начальный период 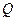, возрастая, достигает некоторого максимума, после чего уменьшается и в переделе становится равным нулю. Площадь, заключенная между осями и кривой, соответствует теплоте, аккумулированной телом за время .

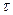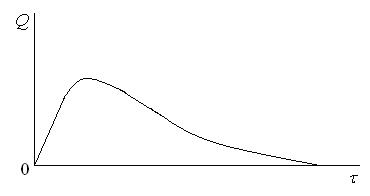
Рисунок 11.6 – Изменение теплового потока при нагреве тела

Аналогичным образом протекают процессы и при охлаждении тела.

Решение задач нестационарной теплопроводности сводится к установлению зависимости изменения температуры и теплового потока во времени для любой точки тела.

11.2.2 Подобие физических процессов

Первое понятие о подобии дается в геометрии, где подобие сводится к масштабам (подобные треугольники).

Может существовать и подобие физических процессов. Рассмотрим явление теплопроводности через однородную плоскую стенку при стационарном режиме. Подобных стенок может быть множество: стенки зданий, паровых котлов и т.д. Материал их различен, различна толщина 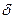, различен температурный перепад в стенке 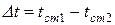. Но теплопроводность всех стенок подчиняется одному и тому же закону Фурье: 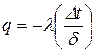. Следовательно, природа явлений одна и та же, таким образом, качественно эти явления одинаковы.

Распределение температур (температурное поле) во всех стенках будет следовать линейному закону. Отсюда вытекает, что процессы теплопроводности для всех однородных плоских стенок при стационарном тепловом режиме будут подобны друг другу.

Чтобы выделить группу подобных явлений или процессов необходимо к математическим (чаще всего дифференциальным) уравнениям присоединить условия однозначности, которые конкретизируют геометрическую форму и размеры устройств, физические свойства среды и тела, начальное состояние тел, особенности протекания на границах тела (граничные условия) и особенности протекания процесса во времени.

Безразмерные комплексы находятся разными способами: методом масштабных преобразований, путем анализа размерностей и пр. Например:

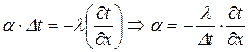- для случая конвективного теплообмена.

Проанализируем размерности: 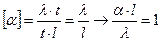- комплекс безразмерный. Этот комплекс называется критерием Био: 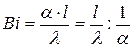- представляет собой соотношение между внутренним 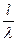и внешним 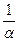тепловыми сопротивлениями. Этот критерий широко используется в теории нестационарной теплопроводности. Критерий 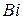тем меньше, чем тоньше тело и чем меньше коэффициент теплоотдачи 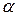и больше коэффициент теплопроводности 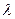. Малым значениям 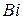< 0,1÷0,25 соответствуют термически тонкие изделия (а не только геометрически тонкие), у которых все точки имеют практически одинаковую температуру. Процесс нагрева (охлаждения) таких изделий называется квазистационарным.

При 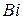> 0,5 изделия будут термически массивными и температура поверхности тела будет отличаться на величину .

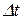При значениях 0,1≤ 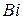≤100 интенсивность нагрева (охлаждения) определяется не только внутренним, но и внешним термическим сопротивлением.

Передачу теплоты при нестационарном режиме можно определить, если найти закон изменения температурного поля и теплового потока во времени и в пространстве:

t = f(x,y,z,τ) и .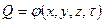

Для аналитического решения уравнения теплопроводности необходимо задание краевых условий:

а) начального распределения температуры в теле;

б) граничных условий, которые могут быть заданы в виде граничных условий третьего рода.

Решение уравнения с учетом граничных и временных условий дает уравнение температурного поля вида

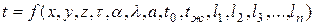. (11.21)

Здесь 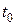- температура тела в начальный момент времени; 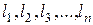- характерные размеры тела.

Однако такое решение может быть получено при целом ряде упрощений и только для твердых тел простой формы – пластины, цилиндра и шара. Для практического использования эти решения представляют в виде графиков и в виде таблиц.

11.2.3 Нагрев неограниченной пластины

Рассмотрим случай нагрева неограниченной пластины. В этом случае тепловой поток движется только вдоль оси х (рис. 11.7) Нестационарный процесс нагрева описывается уравнением Фурье:

,

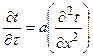Где 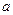- коэффициент температуропроводности, м²/с.

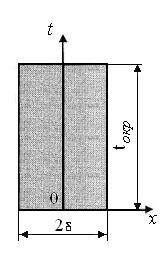
Рисунок 11.7 – к нагреву неограниченной пластины

Если среда, окружающая тело, имеет температуру 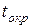, то

,

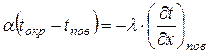где 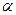- коэффициент теплоотдачи от окружающей среды к поверхности тела, Вт/м²·К.

На распределение температур (11.21) в теле влияет толщина пластины и начальная температура тела.

Переменные уравнения (11.21) можно сгруппировать в безразмерные комплексы, которые носят название чисел подобия.

Этими безразмерными комплексами являются:

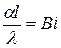- число Био; 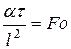- число Фурье; 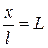- число геометрического подобия (безразмерная координата).

Искомая функция в виде безразмерной температуры:

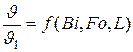, (11.22)

Где 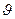- избыточная температура тела, отсчитанная от температуры окружающей среды, т.е. .

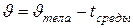При решении технических задач в большинстве случаев достаточно знать температуру на поверхности 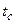и в средней плоскости стенки .

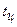Температура поверхности стенки для плоскопараллельной пластины определяется из соотношения:

,

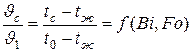Температура в средней плоскости стенки

.

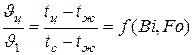11.2.4 Критериальные уравнения теплопроводности

Безразмерную температуру каждой точки пластины толщиной 2 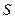при ее двухстороннем нагревании в среде с постоянной температурой 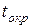можно выразить следующим уравнением:

,

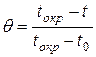где 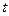- температура в данной точке; 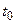- начальная температура, одинаковая во всех точках.

Величину 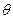можно представить в виде безразмерного уравнения:

;

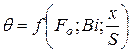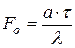- критерий Фурье;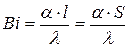

Вместо восьми переменных в уравнении мы получили критериальное уравнение с тремя переменными, что упрощает расчеты.

11.2.5 Регулярный режим нагревания (охлаждения) тел

При нагревании или охлаждении тел наблюдается три этапа:

1) В самом начале нагревания или охлаждения, когда сильно сказывается начальное состояние тела, т.е. начальное распределение температур, процесс носит характер неупорядоченного режима.

2) После интервала вполне определенного промежутка времени на изменение температурного поля перестает влиять начальное состояние тела и наступает регулярный (упорядоченный) тепловой режимнагревания тела. В течение всего времени регулярного режима поле температур остается подобным самому себе, так как во всех точках тела устанавливается изменение температуры с постоянной скоростью.

3) По истечении длительного срока наступает третий режим - стационарный, при котором поле температур тела не изменяется во времени.

При постоянной температуре окружающей среды 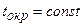скорость изменения температуры в различных местах тела при переходе от одной точки к другой остается постоянной и не зависит от времени.

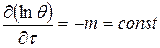
Величину 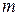называют темпом нагревания (охлаждения), она зависит от формы и размеров тела, а также от термических коэффициентов 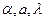, но не зависит ни от координат, ни от времени, будучи одинаковой для всех точек.

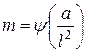, (11.23)

где 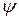- величина, зависящая от критерия 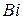и формы тела;

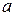- коэффициент температуропроводности тела;

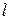- характерный размер.

Так как для пластин 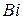<<1, то .

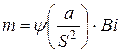Этим простым соотношением можно воспользоваться для экспериментального определения коэффициента температуропроводности.

Пользуясь методом регулярного режима, можно определить также из опыта и другие теплофизические свойства материалов и коэффициентов теплоотдачи.

Если температура среды не постоянна, а изменяется по линейному закону или по периодическому закону, то общим свойством регулярного режима будет соотношение:

,

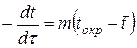где 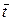- средняя по объему температура тела;

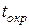- температура среды;

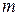- темп нагревания (охлаждения).

Литература: [4], с. 43-47; [5], с. 128-142; [11], с. 28-35; [12], с. 32-39.

Вопросы для самоконтроля

1. Напишите уравнения теплопроводности для однослойной и многослойной стенок.

2. Что такое термическое сопротивление многослойной стенки? В каких единицах оно измеряется?

3. Чем отличаются уравнения теплового потока через твердые предметы различной формы (шар, цилиндр, труба, прямоугольник)?

4. Что такое регулярный режим нагревания (охлаждения) тел?

5. Что такое темп нагревания (охлаждения) тел?