Напряжения в сферических толстостенных сосудах.

На фиг. 547 изображен элемент, вырезанный из толщи стенки толстостенного сферического сосуда; внутренний радиус этого элемента равен r, а наружный 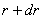; напряжения, действующие на этот элемент, изображены на чертеже.

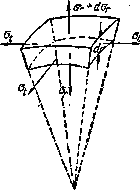
Рис.6. фрагмент сферического толстостенного сосуда.

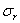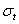Составляя уравнения равновесия и совместности, получаем для и значения:

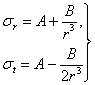
Постоянные А и В могут быть определены из условий на внутренней и внешней поверхностях сосуда пр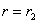и

и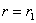

соответственно, где 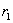и 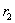— наружный и внутренний радиусы.

Так, при действии внешнего 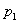и внутреннего 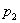давлений А и В определяются из условий:

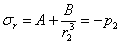на внутренней поверхности,

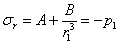на внешней поверхности

Отсюда

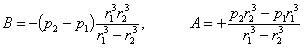
Тогда

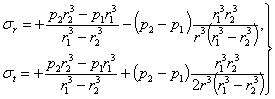
Лекция № 40. Расчет тонкостенных сосудов и резервуаров.

Если толщина стенок цилиндра 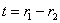мала по сравнению с радиусам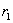и и 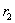, то известное выражение для тангенцальных напряжений приобретает вид

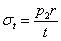
т. е. величину, определенную нами раньше (§ 34).

Для тонкостенных резервуаров, имеющих форму поверхностей вращения и находящихся под внутренним давлением р, распределенным симметрично относительно оси вращения, можно вывести общую формулу для вычисления напряжений.

Выделим (Рис.1) из рассматриваемого резервуара элемент двумя смежными меридиональными сечениями и двумя сечениями, нормальными к меридиану.

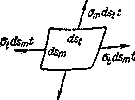
Рис.1. Фрагмент тонкостенного резервуара и его напряженное состояние.

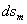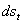Размеры элемента по меридиану и по перпендикулярному к нему направлению обозначим соответственно и , радиусы кривизны меридиана и перпендикулярного к нему сечения обозначим 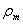и 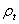, толщину стенки назовем t.

По симметрии по граням выделенного элемента будут действовать только нормальные напряжения 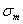в меридиальном направления и 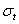в направлении, перпендикулярном к меридиану. Соответствующие усилия, приложенные к граням элемента, будут 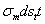и 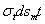. Так как тонкая оболочка сопротивляется только растяжению, подобно гибкой нити, то эти усилия будут направлены по касательной к меридиану и к сечению, нормальному к меридиану.

Усилия 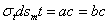(Рис.2) дадут в нормальном к поверхности элемента направлении равнодействующую ab, равную

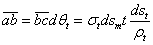
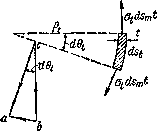
Рис.2. Равновесие элемента тонкостенного резервуара

Подобным же образом усилия 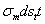дадут в том же направлении равнодействующую 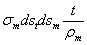Сумма этих усилий уравновешивает нормальное давление, приложенное к элементу

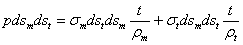
Отсюда

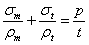
Это основное уравнение, связывающее напряжения 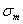и 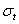для тонкостенных сосудов вращения, дано Лапласом.

Так как мы задались распределением (равномерным) напряжений по толщине стенки, то задача статически определима; второе уравнение равновесия получится, если мы рассмотрим равновесие нижней, отрезанной каким-либо параллельным кругом, части резервуара.

Рассмотрим случай гидростатической нагрузки (рис.3). Меридиональную кривую отнесем к осям х и у с началом координат в вершине кривой. Сечение проведем на уровне у от точки О. Радиус соответствующего параллельного круга будет х.

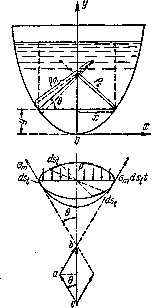
Рис.3. Равновесие нижнего фрагмента тонкостенного резервуара.

Каждая пара усилий 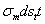, действующих на диаметрально противоположные элементы 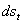проведенного сечения, дает вертикальную равнодействующую bс, равную

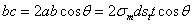
сумма этих усилий, действующих по всей окружности проведенного сечения, будет равна 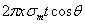; она будет уравновешивать давление жидкости 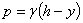на этом уровне плюс вес жидкости в отрезанной части сосуда .

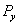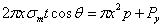
Отсюда

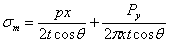
Зная уравнение меридиональной кривой, можно найт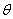и , х и 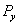для каждого значения у, и стало быть, найти 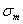, а из уравнения Лапласа и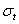

Например, для конического резервуара с углом при вершине 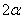, наполненного жидкостью с объемным весом у на высоту h, будем иметь:

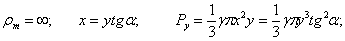
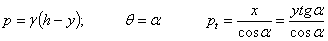
тогда

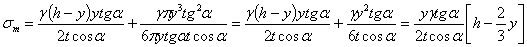
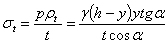
Для сферического сосуда радиусом 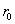, находящегося под внутренним давлением 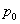, по симметрии 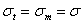; тогда из уравнения (Лапласа), так как

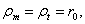
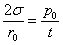и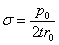

Если меридиональная кривая будет иметь переломы с разрывом непрерывности угла 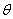, то равновесие тонкой оболочки у места перелома может быть обеспечено лишь наличием реакций, приложенных к оболочке по окружности в этом месте. Появление таких реакций обеспечивается устройством специальных колец, способных брать на себя усилия, возникающие в них в связи с неуравновешенностью напряжений 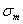по обе стороны точки перелома.

Лекция № 41. Расчет быстровращающегося диска

Значительный интерес представляет задача о напряжениях и деформациях в быстро вращающихся валах и дисках. Высокие скорости вращения валов паровых турбин обусловливают появление в валах и дисках значительных центробежных усилий. Вызванные ими напряжения распределяются симметрично относительно оси вращения диска.

Рассмотрим наиболее простую задачу о расчете диска постоянной толщины. Расчет такого диска положен в основу некоторых приближенных способов расчета дисков любого профиля. Воспользуемся некоторыми результатами, полученными при выводе формул для расчета толстостенных цилиндров. Предположим, что по толщине диска, принимаемой равной единице, напряжения 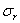и 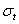не меняются; осевое напряжение 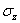будем считать равным нулю.

Составим условия равновесия элемента АВ, выделенного из диска двумя меридиональными сечениями и двумя концентрическими цилиндрическими поверхностями (фиг. 586). В данном случае, кроме сил, действующих по граням элемента АВ, необходимо принять во внимание также и силу инерции

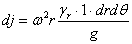
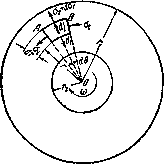
Рис.1. Расчетная схема вращающегося диска.

направленную вдоль радиуса от центра к внешнему контуру диска. Вместо ранее полученного уравнения равновесия получим:

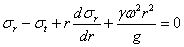(1)

Уравнение условий совместности деформаций также остаются в силе и для данной задачи, т. е.

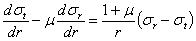(1)

Подставляя в это уравнение значение разности 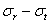из (35.4), находим:

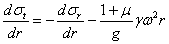(2)

Дифференцируя уравнение (1) по r и подставляя в него вместо 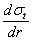его значение из формулы (2), получаем линейное дифференциальное уравнение

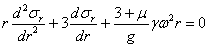
или

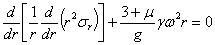
Интегрируя это уравнение, находим:

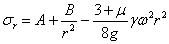(4)

Из (1) и (4) следует, что

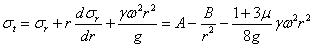(5)

В формулах (4) и (5) А и В — постоянные интегрирования, которые должны быть определены из условий на контуре диска. При определении постоянных рассмотрим два случая: 1) диск с отверстием в центре и 2) сплошной диск. При этом вначале предположим, что края диска свободны от внешних усилий.

Для диска с центральным отверстием напряжение 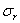должно быть равно нулю как при 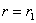, так и при 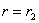(рис.1). Эти условия на контуре при подстановке их в формулу (4) приводят к уравнениям:

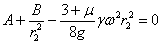
и

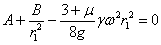
откуда

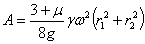и

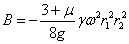
Подставляя значения А и В в формулы (35.7) и (35.8), получаем:

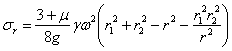
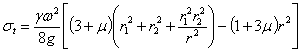
Полагая для краткости можем написать:

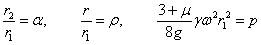и

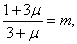
можем написать:

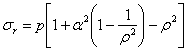
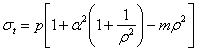
Замечаем, что напряжение 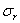обращается в нуль пр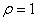и и 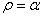, т. е. на внутреннем и наружном контурах диска; при значениях 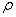между 1 и 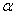напряжение 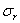положительно и, как нетрудно убедиться, достигает наибольшей величины при 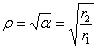При этом

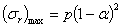(6)

Напряжение 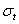при всех значениях 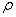также положительно и наибольшей величины достигает у внутреннего края диска, где :

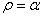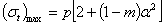(7)

Сравнивая выражения (6) и (7), убеждаемся, что 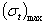всегда больше 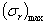Поэтому при проверке прочности диска как по теории наибольших касательных напряжений, так и по энергетической теории условие прочности должно быть написано в таком виде:

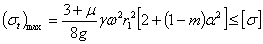
Диск равного сопротивления.

Получено, что, изменение напряжени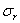й и 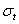вдоль радиуса диска постоянной толщины весьма значительно. Наиболее неравномерное распределение напряжений имеет место в дисках постоянной толщины с отверстием в центре. При расчете подобных дисков приходится ориентироваться на наибольшее напряжение у внутреннего края диска, что сильно ограничивает возможность повышения предельных скоростей. Для достижения высоких скоростей вращения диски приходится делать с переменной толщиной, уменьшающейся от центра к окружности диска. Наиболее выгодным является такой профиль диска, в котором напряжения во всех точках диска сохраняют постоянное значение. Подобные диски называются дисками равного сопротивления. При расчете этих дисков исходят из предположения, что по толщине диска напряжения не меняются, что обычно влечет за собой небольшие погрешности в величинах напряжений.

Основные формулы для расчета дисков переменной толщины по прежнему могут быть выведены из рассмотрения условий равновесия элемента диска abcd.

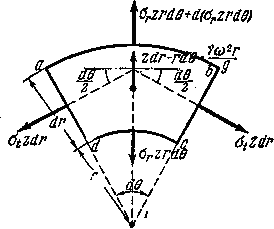
Рис.2. Равновесие элемента диска равного сопротивления.

Переменную толщину диска, являющуюся некоторой функцией радиуса r, обозначим через z. На элемент abcd по меридиональным сечениям ad и bc действуют две силы 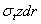, составляющие между собой угол 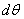; по грани dc на этот элемент действует радиальное усилие 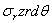, направленное к центру диска, а по грани ab — радиальное усилие 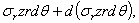, направленное от центра к наружной поверхности диска. К этим усилиям должна быть присоединена еще и сила инерции массы элемента

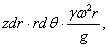
направленная от центра к окружности диска.

Проектируя все перечисленные выше усилия на направление радиуса, получаем такое дифференциальное уравнение равновесия диска переменной толщины:

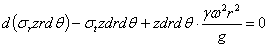
или

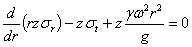
При z = const, это уравнение обращается в известное для диска постоянной толщины.

В случае диска равного сопротивления напряжения 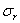и 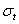всюду постоянны и равны между собой. Приравнивая их величине допускаемого напряжения [ 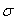], можем так переписать уравнение равновесия:

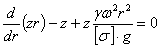
или

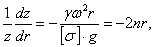
где

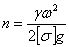
Интегрируя это уравнение, находим:

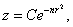
где С — постоянная интегрирования. Если диск не имеет отверстия в центре, то из условия, что при r = 0 z = z₀, следует: С = z₀. Толщина диска в центре (z₀) определяется из условий на контуре диска.

Сплошной диск равного сопротивления может быть применен даже при очень высоких окружных скоростях. Однако по конструктивным соображениям на практике обычно применяются диски переменной толщины с отверстием в центре, профиль которых, близкий к профилю диска равного сопротивления, обеспечивает наиболее выгодное распределение напряжений вдоль радиуса. Методы расчета таких дисков рассматриваются в специальных курсах.

Лекция № 42. Устойчивость сжатых стержней. Формула Эйлера.

Во всем предыдущем изложении мы определяли поперечные размеры стержней из условий прочности. Однако разрушение стержня может произойти не только потому, что будет нарушена прочность, но и оттого, что стержень не сохранит той формы, которая ему придана конструктором; при этом изменится и характер напряженного состояния в стержне.

Наиболее типичным примером является работа стержня, сжатого силами Р. До сих пор для проверки прочности мы имели условие

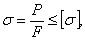
Это условие предполагает, что стержень все время, вплоть до разрушения работает на осевое сжатие. Уже простейший опыт показывает, что далеко не всегда возможно разрушить стержень путем доведения напряжений сжатия до предела текучести или до предела прочности материала.

Если мы подвергнем продольному сжатию тонкую деревянную линейку, то она может сломаться, изогнувшись; перед изломом сжимающие силы, при которых произойдет разрушение линейки, будут значительно меньше тех, которые вызвали бы при простом сжатии напряжение, равное пределу прочности материала. Разрушение линейки произойдет потому, что она не сможет сохранить приданную ей форму прямолинейного, сжатого стержня, а искривится, что вызовет появление изгибающих моментов от сжимающих сил Р и, стало быть, добавочные напряжения от изгиба; линейка потеряет устойчивость.

Поэтому для надежной работы конструкции мало, чтобы она была прочна; надо, чтобы все ее элементы были устойчивы: они должны при действии нагрузок деформироваться в таких пределах, чтобы характер их работы оставался неизменным. Поэтому в целом ряде случаев, в частности, для сжатых стержней, помимо проверки на прочность, необходима и проверка на устойчивость. Для осуществления этой проверки надо ближе ознакомиться с условиями, при которых устойчивость прямолинейной формы сжатого стержня нарушается.

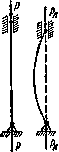
Рис.1. Расчетная схема

Возьмем достаточно длинный по сравнению с его поперечными размерами стержень, шарнирно-прикрепленный к опорам (Рис.1), и нагрузим его сверху центрально силой Р, постепенно возрастающей. Мы увидим, что пока сила Р сравнительно мала, стержень будет сохранять прямолинейную форму. При попытках отклонить его в сторону, например путем приложения кратковременно действующей горизонтальной силы, он будет после ряда колебаний возвращаться к первоначальной прямолинейной форме, как только будет удалена добавочная сила, вызвавшая отклонение.

При постепенном увеличении силы Р стержень будет все медленнее возвращаться к первоначальному положению при проверках его устойчивости; наконец, можно довести силу Р до такой величины, при которой стержень, после небольшого отклонения его в сторону, уже не выпрямится, а останется искривленным. Если мы, не удаляя силы Р, выпрямим стержень, он уже, как правило, не сможет сохранить прямолинейную форму. Другими словами, при этом значении силы Р, называемом критическим 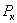, мы будем иметь такое состояние равновесия, когда исключается вероятность сохранения стержнем заданной ему прямолинейной формы).

Переход к критическому значению силы Р происходит внезапно; стоит нам очень немного уменьшить сжимающую силу по сравнению с ее критической величиной, как прямолинейная форма равновесия вновь делается устойчивой.

С другой стороны, при очень небольшом превышении сжимающей силой Р ее критического значения прямолинейная форма стержня делается крайне неустойчивой; достаточно при этом небольшого эксцентриситета приложенной силы, неоднородности материала по сечению, чтобы стержень искривился, и не только не вернулся к прежней форме, а продолжал искривляться под действием все возрастающих при искривлении изгибающих моментов; процесс искривления заканчивается либо достижением совершенно новой (устойчивой) формы равновесия, либо разрушением.

Исходя из этого, мы должны практически считать критическую величину сжимающей силы 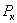эквивалентной нагрузке, «разрушающей» сжатый стержень, выводящей его (и связанную с ним конструкцию) из условий нормальной работы. Конечно, при этом надо помнить, что «разрушение» стержня нагрузкой, превышающей критическую, может происходить при непременном условии беспрепятственного возрастания искривления стержня; поэтому если при боковом выпучивании стержень встретит боковую опору, ограничивающую его дальнейшее искривление, то разрушение может и не наступить.

Обычно подобная возможность является исключением; поэтому практически следует считать критическую сжимающую силу низшим пределом «разрушающей» стержень силы.

Рис.2. Аналогия понятия устойчивости из механики твердого тела

Явление потери устойчивости при сжатии можно по аналогии иллюстрировать следующим примером из механики твердого тела (рис.2). Будем вкатывать цилиндр на наклонную плоскость ab, которая потом переходит в короткую горизонтальную площадку bс и наклонную плоскость обратного направления cd. Пока мы поднимаем цилиндр по плоскости ab, поддерживая его при помощи упора, перпендикулярного к наклонной плоскости, он будет в.состоянии устойчивого равновесия; на площадке bс его равновесие делается безразличным; стоит же нам поместить цилиндр в точку с, как его равновесие сделается неустойчивым— при малейшем толчке вправо цилиндр начнет двигаться вниз.

Описанную выше физическую картину потери устойчивости сжатым стержнем легко осуществить в действительности в любой механической лаборатории на очень элементарной установке. Это описание не является какой-то теоретической, идеализированной схемой, а отражает поведение реального стержня под действием сжимающих сил.

Потерю устойчивости прямолинейной формы сжатого стержня иногда называют «продольным изгибом», так как она влечет за собой значительное искривление стержня под действием продольных сил. Для проверки на устойчивость сохранился и до сих пор термин «проверка на продольный изгиб», являющийся условным, так как здесь речь должна идти не о проверке на изгиб, а о проверке на устойчивость прямолинейной формы стержня.

Установив понятие о критической силе, как о «разрушающей» нагрузке, выводящей стержень из условий его нормальной работы, мы легко можем составить условие для проверки на устойчивость, аналогичное условию прочности.

Критическая сила 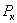вызывает в сжатом стержне напряжение, называемое «критическим напряжением» и обозначаемое буквой 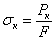. Критические напряжения являются опасными напряжениями для сжатого стержня. Поэтому, чтобы обеспечить устойчивость прямолинейной формы стержня, сжатого силами Р, необходимо к условию прочности 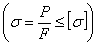добавить еще условие устойчивости:

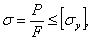
где 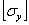— допускаемое напряжение на устойчивость, равное критическому, деленному на коэффициент запаса на устойчивость, т. е. .

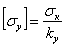Для возможности осуществить проверку на устойчивость мы должны показать, как определять 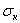и как выбрать коэффициент запаса .

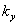Формула Эйлера для определения критической силы.

Для нахождения критических напряжений 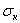надо вычислить критическую силу 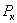, т. е. наименьшую осевую сжимающую силу, способную удержать в равновесии слегка искривленный сжатый стержень.

Эту задачу впервые решил академик Петербургской Академии наук Л. Эйлер в 1744 году.

Заметим, что самая постановка задачи иная, чем во всех ранее рассмотренных отделах курса. Если раньше мы определяли деформацию стержня при заданных внешних нагрузках, то здесь ставится обратная задача: задавшись искривлением оси сжатого стержня, следует определить, при каком значении осевой сжимающей силы Р такое искривление возможно.

Рассмотрим прямой стержень постоянного сечения, шарнирно опертый по концам; одна из опор допускает возможность продольного перемещения соответствующего конца стержня (рис.3). Собственным весом стержня пренебрегаем.

Рис.3. Расчетная схема в «задаче Эйлера»

Нагрузим стержень центрально приложенными продольными сжимающими силами 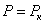и дадим ему весьма небольшое искривление в плоскости наименьшей жесткости; стержень удерживается в искривленном состоянии, что возможно, так как .

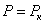Деформация изгиба стержня предположена весьма малой, поэтому для решения поставленной задачи можно воспользоваться приближенным дифференциальным уравнением изогнутой оси стержня. Выбрав начало координат в точке А и направление координатных осей, как показано на рис.3, имеем:

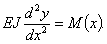(1)

Возьмем сечение на расстоянии х от начала координат; ордината изогнутой оси в этом сечении будет у, а изгибающий момент равен

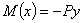
По исходной схеме изгибающий момент получается отрицательным, ординаты же при выбранном направлении оси у оказываются положительными. (Если бы стержень искривился выпуклостью книзу, то момент был бы положительным, а у — отрицательным и .)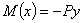

Приведенное только что дифференциальное уравнение принимает вид:

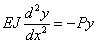
деля обе части уравнения на EJ и обозначая дробь 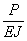через 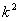приводим его к виду:

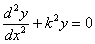
Общий интеграл этого уравнения имеет вид:

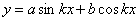
Это решение заключает в себе три неизвестных: постоянные интегрирования а и b и значение 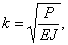, так как величина критической силы нам неизвестна.

Краевые условия на концах стержня дают два уравнения:

в точке А при х = 0 прогиб у = 0,

В х = 1 у = 0.

Из первого условия следует (так как 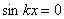и cos kx =1)

0 = b.

Таким образом, изогнутая ось является синусоидой с уравнением

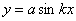(2)

Применяя второе условие, подставляем в это уравнение

у = 0 и х = l

получаем:

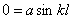
Отсюда следует, что или а или kl равны нулю.

Если а равно нулю, то из уравнения (2) следует, что прогиб в любом сечении стержня равен нулю, т. е. стержень остался прямым. Это противоречит исходным предпосылкам нашего вывода. Следовательно, sin kl = 0, и величина 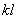может иметь следующий бесконечный ряд значений:

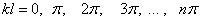
где 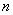— любое целое число.

Отсюда 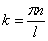, а так как 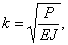то

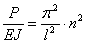и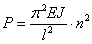

Иначе говоря, нагрузка, способная удержать слегка искривленный стержень в равновесии, теоретически может иметь целый ряд значений. Но так как отыскивается, и интересно с практической точки зрения, наименьшее значение осевой сжимающей силы, при которой становится возможным продольный изгиб, то следует принять .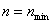

Первый корень 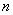=0 требует, чтобы 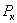было равно нулю, что не отвечает исходным данным задачи; поэтому этот корень должен быть отброшен и наименьшим корнем принимается значение 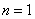. Тогда получаем выражение для критической силы:

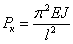(3)

(Здесь J—минимальный момент инерции поперечного сечения стержня.) Это — так называемая формула Эйлера для сжатого стержня с шарнирно-опертыми концами. Значению критической силы (3) соответствует изгиб стержня по синусоиде с одной полуволной [формула (2)]

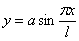
Лекция № 43. Анализ формулы Эйлера

Значениям критической силы высших порядков соответствуют искривления по синусоидам с двумя, тремя и т. д. полуволнами (Рис.1):

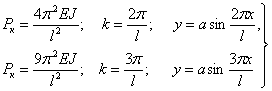(1)

Таким образом, чем больше точек перегиба будет иметь синусоидально-искривленная ось стержня, тем большей должна быть критическая сила. Более полные исследования показывают, что формы равновесия, определяемые формулами (1), неустойчивы; они переходят в устойчивые формы лишь при наличии промежуточных опор в точках В и С (рис.1).

Рис.1

Таким образом, поставленная задача решена; для нашего стержня наименьшая критическая сила определяется формулой

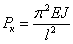
а изогнутая ось представляет синусоиду

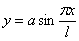
Величина постоянной интегрирования а осталась неопределенной; физическое значение ее выяснится, если в уравнении синусоиды положить 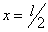; тогда 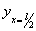(т. е. посредине длины стержня) получит значение:

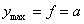
Значит, а — это прогиб стержня в сечении посредине его длины. Так как при критическом значении силы Р равновесие изогнутого стержня возможно при различных отклонениях его от прямолинейной формы, лишь бы эти отклонения были малыми, то естественно, что прогиб f остался неопределенным.

Он должен быть при этом настолько малым, чтобы мы имели право применять приближенное дифференциальное уравнение изогнутой оси, т. е. чтобы 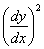было по прежнему мало по сравнению с единицей.

Получив значение критической силы, мы можем сейчас же найти и величину критического напряжения 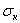, разделив силу 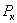на площадь сечения стержня F; так как величина критической силы определялась из рассмотрения деформаций стержня, на которых местные ослабления площади сечения сказываются крайне слабо, то в формулу для 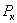входит момент инерции 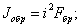поэтому принято при вычислении критических напряжений, а также при составлении условия устойчивости вводить в расчет полную, а не ослабленную, площадь поперечного сечения стержня 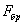. Тогда

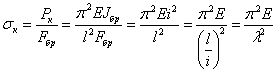
Таким образом, критическое напряжение для стержней данного материала обратно пропорционально квадрату отношения длины стержня к наименьшему радиусу инерции его поперечного сечения. Это отношение 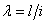называется гибкостью стержня и играет весьма важную роль во всех проверках сжатых стержней на устойчивость.

Из последнего выражения видно видно, что критическое напряжение при тонких и длинных стержнях может быть весьма малым, ниже основного допускаемого напряжения на прочность 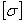. Так, для стали 3 с пределом прочности 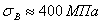допускаемое напряжение может быть принято 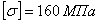; критическое же напряжение для стержня с гибкостью 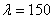при модуле упругости материала 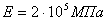будет равно

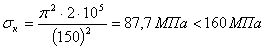
Таким образом, если бы площадь сжатого стержня с такой гибкостью была подобрана лишь по условию прочности, то стержень разрушился бы от потери устойчивости прямолинейной формы.