Сравнение систем автоматического управления - классической одноконтурной и интеллектуальной с fuzzy-регулятором.
Выше была рассмотрена система управления на основе ПИД – регулятора. Дополним ее блоком нечеткого управления и сравним показатели переходных процессов обеих систем. Построим модель одноконтурной системы автоматического регулирования с ПИД-регулятором в обратной связи (Рис.14.1). На вход подается единичное ступенчатое воздействие.
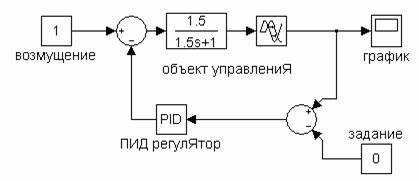
Рис.14.1. Модель одноконтурной системы автоматического регулирования
Объект управления представляет собой последовательное соединение типовых звеньев автоматики: апериодического звена первого порядка и звена запаздывания.
Значения параметров настройки ПИД-регулятора для данного объекта следующие: P= 1.093, I =1/TИ =0.86, D=TД=0.209.
Для реализации модели ПИД - подобного fuzzy-регулятора необходимо собрать следующую структурную (Рис.14.2). Библиотека системы Simulink содержит необходимый нам блок fuzzy-регулятора.
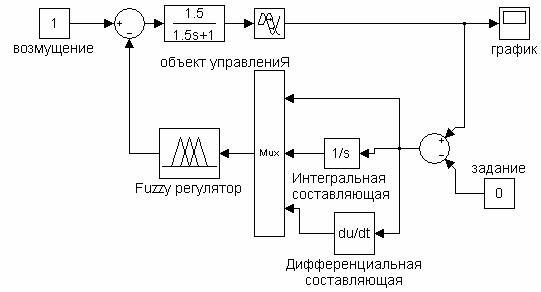
Рис.14.2. Модель одноконтурной системы автоматического регулирования с ПИД-fuzzy-регулятором.
Командой fuzzy в окне MATLAB вызываем окно Редактора фаззи-инференционной системы (FuzzyInferenceSystemEditor), выбираем тип системы - Мамдани, задаём три входа - для пропорциональной, интегральной и дифференциальной составляющих и называем входные переменные, например, p, i и d, а выходную - y.
Из данного окна вызываем окно Редактора функций принадлежности (MembershipFunctionEditor) двойным щелчком мыши по изображению переменной p или при помощи меню Edit. Здесь для лингвистического описания каждой переменной выберем семь треугольных термов (NB,NM,NS,ZE,PS,PM,PB). Термы выходной переменной лучше выбирать непересекающимися. Это повысит чёткость регулирования. В этом же окне зададим диапазоны изменения переменных.Для входных переменных регулятора рекомендуются симметричные диапазоны изменения, при этом p [-1/P : 1/P], i [-1/I : 1/I], d [-1 : 1]. y [0 : C], где верхняя граница С при единичном ступенчатом воздействии варьируется от 1.1 до 2, чтобы выходной сигнал регулятора мог компенсировать это возмущение. По мере увеличения значения С уменьшается динамическая ошибка, но возрастают время регулирования и число колебаний переходного процесса. Поэтому рекомендуется С принимать равным 2, когда наблюдается оптимальное соотношение между величиной динамической ошибки, времени регулирования и количеством колебаний. Возможный видфункций принадлежности входной переменной p представлен на Рис.14.3.
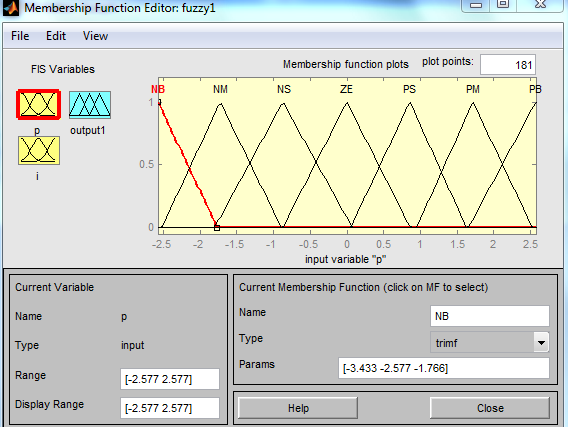
Рис.14.3.Функции принадлежности входной переменной p.
Возможный видфункций принадлежности входной переменной i представлен на Рис.14.4.
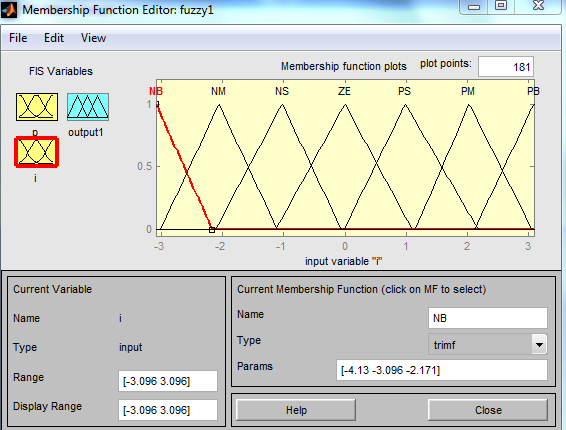
Рис.14.4.Функции принадлежности входной переменной i.
Возможный видфункций принадлежности входной переменной output1 представлен на Рис.14.5.
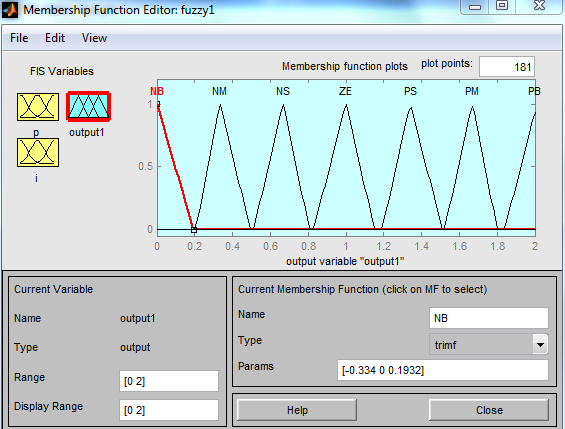
Рис.14.5 .Функции принадлежности выходной переменнойoutput1.
Теперь необходимо сформировать базу правил fuzzy-регулятора. Линейный непрерывный ПИ-регулятор можно заменить близким по логике управления fuzzy-регулятором, если в качестве его выходной переменной рассматривать приращение управляющего воздействия Δy. Для входных переменных ε(k) и Δε(k) и выходной Δy(k) может быть синтезирован fuzzy-регулятор, реализующий нелинейный закон ∆y = F(∆ε(k), ε(k)), эквивалентный в определённом смысле ПИ-регулятору.
Таблица14.1 Система правил нечеткого вывода.
 ε ∆ε ε ∆ε | NB | NM | NS | ZE | PS | PM | PB |
| NB | NB | NB | NB | NB | NM | NS | ZE |
| NM | NB | NB | NB | NM | NS | ZE | PS |
| NS | NB | NB | NM | NS | ZE | PS | PM |
| ZE | NB | NM | NS | ZE | PS | PM | PB |
| PS | NM | NS | ZE | PS | PM | PB | PB |
| PM | NS | ZE | PS | PM | PB | PB | PB |
| PB | ZE | PS | PM | PB | PB | PB | PB |
Для нашего случая p соответствует сигналу рассогласования ε(k), i соответствует приращению сигнала рассогласования Δε(k), а ouput1 соответствует Δy(k). Лингвистические правила для такого ПИ-подобного fuzzy-регулятора приведены в таблице 14.1.
Вызываем окно Редактора правил (RuleEditor) в меню Edit и заполняем список правилами из таблицы 1. Можно посмотреть пространство управления, вызвав окно Просмотра пространства управления(SurfaceViewer) из меню View или комбинацией клавиш Ctrl+6. Полученный файл сохраним под именем fuzzy1.fis.
В окне параметров блока FuzzyLogicController укажем имя файла fuzzy1. В окне модели в меню File выберем пункт ModelProperties. В открывшемся окне выберем вкладку CallBacks и в поле Modelpre-loadfunction напишем: fuzzy1=readfis('fuzzy1').
Данная команда каждый раз при открытии файла модели будет помещать файл fuzzy1.fisв WorkSpace- рабочее пространство системы MATLAB. Это необходимо для нормальногофункционирования модели. При внесении изменений в fis-файл нужно помещать его исправленную версию в WorkSpace либо при помощи пункта Export/ToWorkspace меню File, либо комбинацией клавиш Ctrl+T, либо каждый раз закрытием и открытием файла модели.
В диалоговом окне Simulation Parametersменю Simulationво вкладке Advancedдля опции Boolean logic signalsнеобходимо установить значение off. При этом блоки логики будут допускать переменные в форме с плавающей точкой.
За основу fis-файла, реализующего ПИД- закон регулирования, может быть взят файл fuzzy1.fis. В окне Редактора фаззи - системы добавим ещё одну входную переменную d. В окне Редактора функций принадлежности зададим три треугольных терма для описания этой переменной - N, ZE и P, Рис.14.6.
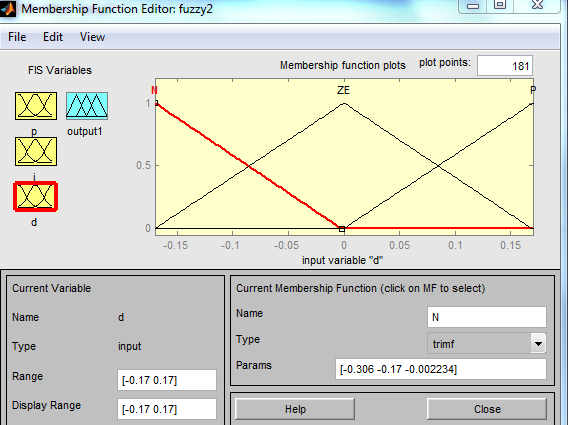
Рис.14.6.Функции принадлежности входной переменной d.
Для новой выходной переменной output1добавим два терма N и P, (Рис.14.7).
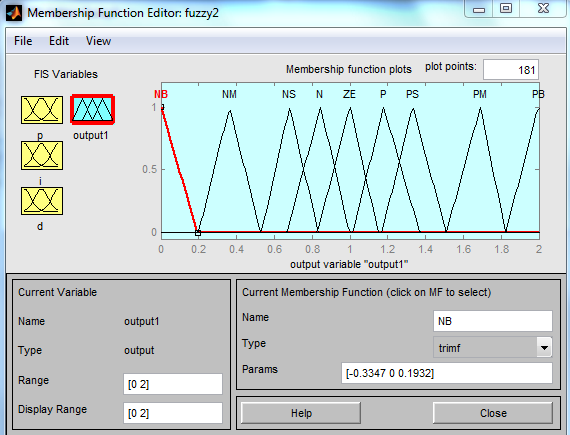
Рис.14.7.Функции принадлежности новой выходной переменнойПИД-подобного fuzzy-регулятораoutput1.
Диапазоны изменения переменных:
· p=[-0.915;0.915]
- i=[-1.163;1.163]
- d=[-1;1] (первоначально)
- output1=[0;2]
В окне Редактора правил дополняем список правил следующими тремя правилами:
- IF (p=N) THEN (output1=N)
- IF (i=ZE) THEN (output1=ZE)
- IF (d=P) THEN (output1=P)
Действительно, если скорость положительна, то выходной сигнал регулятора должен увеличиться, чтобы предупредить увеличение сигнала рассогласования, и наоборот.
Теперь сохраним отредактированный файл под именем fuzzy2.fis. В окне параметров блока FuzzyLogicController модели укажем имя файла fuzzy2. В окне модели в меню File выберем пункт ModelProperties. В открывшемся окне выберем вкладку CallBacks и в поле Modelpre-loadfunction напишем: fuzzy2=readfis('fuzzy2').
ВдиалоговомокнеSimulation ParametersменюSimulationвовкладкеAdvancedдляопцииBoolean logic signalsнеобходимоустановитьзначениеoff.
Более точная настройка диапазона изменения D-составляющей осуществляется методом подбора. Например, для данного объекта [-0.16;0.16].
Графики переходных процессов для модели с аналоговым регулятором и модели с ПИД - подобным fuzzy-регулятором представлены на Рис.14.8.
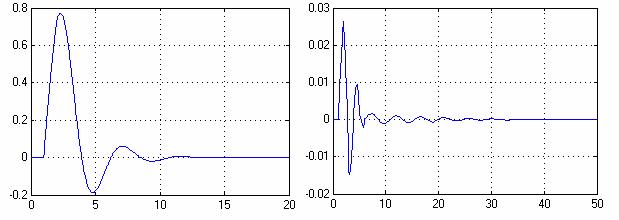
Рис.14.8. Графики переходных процессов для модели с аналоговым регулятором (а) и модели с ПИД - fuzzy-регулятором
Из Рис.14.8 видим, что время регулирования и число колебаний больше для системы с fuzzy-регулятором, однако динамическая ошибка значительно уменьшилась. Наличие D-составляющей должно уменьшить динамическую ошибку системы.
