Внутренняя устойчивость линейных систем

Ранее фактически рассматривалась техническую устойчивость, то есть устойчивость по выходу при ненулевых начальных условиях. Теперь посмотрим, как определить внутреннюю устойчивостьлинейной системы, то есть устойчивость внутренних процессов. Поскольку выход системы нас не интересует, используем модель «вход-состояние»:

x’ (t) = Ax(t) + Bu(t) ,

где x(t) – вектор состояния, u(t) – входной сигнал, A и B – постоянные матрицы. Если входравен нулю (нет возмущений), уравнение упрощается:

x’(t) = Ax(t) .

Таким образом, свободное движение определяется только свойствами матрицы A. Если считать, чтоматрица A имеет вид

,

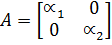тогда получим два независимых уравнения:

x’₁(t) = α₁x(t),x’₂(t) = α₂x(t)

Здесь устойчивость определяется значениями α₁и α₂. Если они оба отрицательны, то система асимптотически устойчива. Если одно из них – нуль, а второе отрицательно (или оба нулевых), то система нейтрально устойчива.

В общем случае внутренняя устойчивость зависит от собственных чиселматрицы A , то есть, от корней характеристического уравненияdet(λI− A) = 0, где I – единичная матрица, а «det» обозначает определитель квадратной матрицы. Полином det(λI− A) от переменной λ называют характеристическим полиномом. Например, для рассмотренной выше диагональной матрицы A

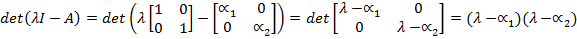
Корни этого полинома –α₁и α₂. Если все корни характеристического полинома устойчивы (имеют отрицательные вещественные части, расположены в левой полуплоскости), то система асимптотически устойчива. Если есть неустойчивые корни (с положительной вещественной частью), то система неустойчива. Если характеристический полином имеет один нулевой корень или пару комплексно-сопряженных корней на мнимой оси, система нейтрально устойчива.

Внутренняя устойчивость – более сильное требование, чем техническая устойчивость, потому что определяет ограниченность не только выхода, но и всех внутренних переменных при любых начальных условиях.

Критерии устойчивости

Для исследования устойчивости линейной системы достаточно найти корни ее характеристического полинома. Однако вычисления корней характеристического полинома дает только количественные, а не качественные результаты и не позволяет исследовать устойчивость теоретически, например, определять границы областей устойчивости.Необходимые и достаточные условия дают алгебраические критерии Рауса и Гурвица.

Критерий Рауса

Раус предложил критерий устойчивости систем автоматического управления в виде алгоритма, по которому заполняется специальная таблица с использованием коэффициентов характеристического уравнения:

1) в первой строке записываются коэффициенты уравнения с четными индексами в порядке их возрастания;

2) во второй строке - с нечетными;

3) остальные элементы таблицы определяется по формуле: c_k,i = c_{k+ 1,i - 2}–

ri c_{k+ 1,i - 1}, где ri = c_{1,i - 2}/c_{1,i - 1}, i 3 - номер строки, k - номер столбца.

4) Число строк таблицы Рауса на единицу больше порядка характеристического уравнения.

Ri	i\k
-		c11 = a0	c21 = a2	c31 = a4	...
-		c12 = a1	c22 = a3	c32 = a5	...
r3 = c11/cc12		c13 = c21-r3c22	c23 = c31-r3c32	c33 = c41-r3c42	...
r3 = c11/c12		c14 = c22-r3c23	c24 = c32-r4c33	c34 = c42-r4c43	...
...	...	...	...	...	...

Критерий Рауса: для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Раусаc₁₁, c₁₂, c₁₃,... были положительными. Если это не выполняется, то система неустойчива, а количество правых корней равно числу перемен знака в первом столбце.

Достоинство - критерий прост в использовании независимо от порядка характеристического уравнения. Он удобен для использования на ЭВМНедостаток - малая наглядность, трудно судить о степени устойчивости системы, насколько далеко отстоит она от границы устойчивости.

Критерий Гурвица

Гурвиц предложил другой критерий устойчивости. Из коэффициентов характеристического уравнения строится определитель Гурвица 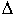по алгоритму:

1) по главной диагонали слева направо выставляются все коэффициенты характеристического уравнения от a₁ до a_n;

2) от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз;

3) на место коэффициентов с индексами меньше нуля или больше n ставятся нули.

Критерий Гурвица: для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы все n диагональных миноров определителя Гурвица были положительны. Эти миноры называются определителями Гурвица.

Рассмотрим примеры применения критерия Гурвица:

1) n = 1 => уравнение динамики: a₀p + a₁ = 0. Определитель Гурвица: 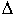= 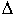₁ = a₁ > 0 при a₀ > 0, то есть условие устойчивости:a₀> 0, a₁ > 0;

2)n = 2 => уравнение динамики: a₀p² + a₁p + a₂ = 0. Определители Гурвица: 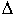₁ = a₁> 0, D₂ = a₁a₂ - a₀a₃ = a₁a₂ > 0, так как a₃ = 0, то есть условие устойчивости: a₀> 0, a₁> 0, a₂ > 0;

3) n = 3 =>уравнениединамики: a₀p³ + a₁p² + a₂p + a₃ = 0. ОпределителиГурвица: 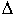₁ = a₁> 0, 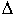₂ = a₁a₂ - a₀a₃ > 0, 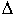3 = a_{3 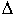2} > 0, условиеустойчивости: a₀ > 0, a₁ > 0, a₂ > 0, a₃ > 0, a₁a₂ - a₀a₃ > 0;

Таким образом при n 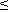2 положительность коэффициентов характеристического уравнения является необходимым и достаточным условием устойчивости систем управления. При n > 2 появляются дополнительные условия.

Критерий Гурвица применяют приn 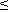4.При больших порядках возрастает число определителей и процесс становится трудоемким. Имеется ряд модификаций данного критерия, расширяющие его возможности.

Недостаток критерия Гурвица - малая наглядность. Достоинство - удобен для реализации на ЭВМ. Его часто используют для определения влияния одного из параметров САУ на ее устойчивость. Так равенство нулю главного определителя 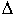_n = a_{n 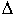n-1} = 0 говорит о том, что система находится на границе устойчивости. При этом либо a_n = 0 - при выполнении остальных условий система находится на границе апериодической устойчивости, либо предпоследний минор 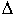_n-1 = 0 - при положительности всех остальных миноров система находится на границе колебательной устойчивости. Параметры САУ определяют значения коэффициентов уравнения динамики, следовательно изменение любого параметра Ki влияет на значение определителя 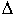_n-1. Исследуя это влияние можно найти, при каком значении Ki определитель 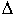_n-1 станет равен нулю, а потом - отрицательным. Это и будет предельное значение исследуемого параметра, после которого система становится неустойчивой.

Критерий Найквиста

Критерий Найквиста позволяет определить устойчивость замкнутой системы, Рис.7.8, построив частотную характеристику разомкнутойсистемы. Пусть L(s) – передаточная функция разомкнутой системы, а L(jω) – ее частотная характеристика.

Рис.7.8. Замкнутая система управления.

Сначала будем считать, что разомкнутая система устойчива и не содержит интегрирующих звеньев, то есть L(0) = K ≠ ∞, где K – некоторое число. Для каждой частоты ω значение L( jω) – это комплексное число, которое можно изобразить точкой на комплексной плоскости. При изменении частоты от 0 до∞ из этих точек складывается годограф Найквиста– некоторая кривая, которая начинается в точке (K; 0) на вещественной оси и заканчивается в начале координат (если L(s) – строго правильная функция, то есть степень ее числителя меньше степени знаменателя). Можно доказать, что система устойчива тогда и только тогда, когда годограф L( jω) не охватывает точку (−1; 0) . На рисунке слева годограф не охватывает эту точку (и замкнутая система устойчива), а на рисунке справа – охватывает (система неустойчива).

Рис.7.9. Устойчивость по Найквисту.

Выражение «система находится на границе устойчивости» означает, что частотная характеристика проходит через точку (−1; 0), Рис.7.10. В этом случае для некоторой частоты ω имеемA(ω) =1 и φ(ω) = −180°. Это говорит о том, что после прохождения контура величина сигналаменяет знак, сохраняя абсолютную величину (энергию), то есть устанавливаются незатухающиеколебания.

Рис.7.10. Система на границе устойчивости.

Частота ω_c, для которой A(ω_с) = 1, называется частотой среза. Для устойчивой системызначение фазы на частоте среза должно быть больше, чем −180°; в этом случае годограф неохватит точку (−1; 0), Рис.7.11.

Рис.7.11. Система устойчивая по Найквисту.

Если передаточная функция L(s) имеет полюса в точке s = 0 (то есть обращается в бесконечность в этой точке), ситуация усложняется Рис.7.12. Теперь годограф начинается не на вещественной оси, а приходит из бесконечности. Тогда в контур необходимо включить не только полученную кривую, но и часть окружности бесконечного радиуса от вещественной оси до годографа в порядке обхода по часовой стрелке. Если функция L(s) имеет k полюсов в точке s = 0, нужно добавить k секторов по 90°. На рисунках показаны годографы Найквиста устойчивых систем, в которых функция L(s) имеет соответственно 1 и 2 полюса в точке s = 0. Эти годографы не охватывают точку (−1; 0) .

Рис.7.12. Полюс передаточной функции в точке 0.

Если в системе есть запаздывание на время τ, на любой частоте появляется дополнительный сдвиг фазы на−τω(без изменения амплитуды). Это значит, что каждая точка годографа поворачивается на некоторый угол против часовой стрелки, Рис.7.13.

Рис.7.13. Система с запаздыванием.

На рисунке короткая линия – частотная характеристика системы без запаздывания, а длинная – аналогичная характеристика для системы с запаздыванием. Видно, что запаздывание привело к неустойчивости системы (годограф охватил критическую точку (−1; 0)). Таким образом, система может потерять устойчивость из-за «медленного» датчика. Можно сказать, что запаздывание всегда ухудшает устойчивость системы, и этот факт важно учитывать при проектировании.

Если L(s) имеет полюса с положительной вещественной частью (разомкнутая системанеустойчива), нужно считать, сколько раз годограф пересекает ось абсцисс левее точки (−1; 0) .Причем переходы «сверху вниз» считаются положительными, а переходы «снизу вверх» - отрицательными.

Для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы разница между числом положительных и отрицательных переходов была равна l /2, где l – число неустойчивых полюсов функции L(s). Начальная точка на оси абсцисс левее точки (−1; 0) считается за половину перехода. На Рис.7.14показаны годографы устойчивых систем для случая

l= 1.

Рис.7.14. Годографы устойчивых систем для случаяl= 1.

Частотная характеристика начинается на вещественной оси левее точки (−1; 0). На рисунке слева годограф сначала идет вниз (половина положительного перехода) и больше нигде не пересекает ось абсцисс левее точки (−1; 0) , поэтому разница переходов равна 1/ 2 = l / 2 и замкнутая система устойчива.

На правом рисунке частотная характеристика сначала идет вверх (считаем это за половину отрицательного перехода), а затем переходит в нижнюю полуплоскость (положительный переход). Разница снова равна 1/ 2 = l /2 и система устойчива.

Переходные процессы

Хорошо спроектированная система должна не только быть устойчивой и поддерживать заданную точность в установившемся режиме, но и плавно переходить на новый режим при изменении заданного значения выхода (уставки). Качество переходных процессов обычно оценивается по переходной характеристике (реакции системы на единичный ступенчатый входной сигнал), Рис.7.15.

Рис.7.15. Переходные характеристики систем.

Важно, насколько быстро заканчивается переход на другой режим (время переходного процесса t_n). Оно определяется как время, через которое регулируемая величина входит в коридор шириной 2Δ вокруг установившегося значения y∞. Это значит, что при t >t_nзначение выхода отличается от установившегося не более, чем на Δ. Обычно величина Δ задается в процентах от установившегося значения, чаще всего 2% или 5%. Для апериодического звена с постоянной времени T время переходного процесса равно t_n= 3 T(с точностью 5%).

Другая важная характеристика – перерегулированиеσ – показывает, на сколько процентов максимальное значение выхода y_max превышает установившееся значение y∞:

.

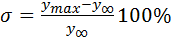Иногда удается обеспечить нулевое перерегулирование (апериодический переходный процесс, как у апериодического звена). Увеличение быстродействия обычно приводит к увеличению перерегулирования.

Частотные оценки качества

Качество системы можно оценивать не только во временнóй области (переходный процесс во времени), но и в частотной (по частотной характеристике). Из частотных оценок наиболее важны запасы устойчивости. Дело в том, что поведение реального объекта всегда несколько отличается от принятой модели, более того, динамика может меняться во времени, например, когда корабль или ракета расходует топливо во время движения. Поэтому недостаточно спроектировать просто устойчивую систему, нужно, чтобы система сохранила устойчивость при некоторых изменениях параметров объекта и регулятора в сравнении с расчетными, то есть обладала запасами устойчивости.

Обычно рассматривают запасы устойчивости по амплитуде и по фазе. Запас устойчивости по амплитудеg_m– это дополнительное усиление контура, которое необходимо, чтобы вывести систему на границу области устойчивости. Эта величина измеряется в децибелах, Рис.7.16.

Рис.7.16. Запас устойчивости по амплитуде.

Запас по амплитуде вычисляется по формуле 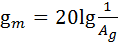, где A_g< 1– значение амплитуднойхарактеристики на частоте ω_g, где фазовая характеристика равна −180°. В практических задачах обеспечивают запас по амплитуде не менее 6 дБ.

Запас устойчивости по фазеφ_m– это дополнительный сдвиг фазы («поворот» частотной характеристики против часовой стрелки), который необходим для того, чтобы вывести системуна границу устойчивости. Он определяется на ω_c, где A(ω_c )= 1. Запас по фазе должен быть не менее 30°.

В некоторых случаях классические запасы устойчивости (по амплитуде и фазе) дают не совсем верное представление о том, насколько система действительно близка к границе устойчивости. Поэтому в качестве единой характеристики иногда используют кратчайшее расстояние γ от годографа до точки (−1; 0) .

Рис.7.17. Запас устойчивости по фазе.

Еще одна аналогичная характеристика называется показателем колебательностиM. Она определяется по амплитудной частотной характеристике замкнутой системы как отношение ее максимума к значению на нулевой частоте, Рис.7.18.

Рис.7.18. Амплитудная частотная характеристика замкнутой системы.

Для каждого значения M можно нарисовать «запретную область», в которую не должназаходить частотная характеристика разомкнутой системы, если ее показатель колебательностидолжен быть меньше М. Эта область имеет форму круга радиуса 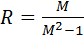, центр которого находится в точке 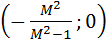. На Рис.7.19 показаны границы запретных областей для различных значений M.

Рис.7.19. Границы запретных областей для различных значений M.

При M = 1 окружность имеет бесконечный радиус (превращается в вертикальную линию) и проходит через точку (−0,5; 0) . При увеличении M радиус окружности уменьшается.

Корневые оценки качества

Многие свойства системы можно предсказать, посмотрев на расположение корнейхарактеристического полинома Δ(s) на комплексной плоскости. Прежде всего, все корни Δ(s) для устойчивой системы должны находиться в левой полуплоскости, то есть слева от мнимой оси. Быстродействие системы определяется степенью устойчивостиη – так называется расстояние от мнимой оси до ближайшего корня (или пары комплексно-сопряженных корней).

На Рис.7.20 точками отмечены положения корней характеристического полинома. Он имеет два вещественных корня (обозначенных номерами 1 и 4) и пару комплексно сопряженных корней (2 и 3). Степень устойчивости определяется вещественным корнем 1, потому что он находится ближе всех к мнимой оси.

Рис.7.20.Положения корней характеристического полинома.

Этот корень называется доминирующим, он определяет самые медленные движения в системе и время переходного процесса, которое может быть примерно рассчитано по формуле tn = 3/η. Корни 2, 3 и 4 соответствуют более быстрым движениям. Степень устойчивости, несмотря на название, ничего не говорит о близости системы к границе устойчивости, она только характеризует быстродействие.

Параметр, определяющий скорость затухания колебаний в системе, называется колебательностью. Колебательностьμ для пары комплексно-сопряженных корней α ± jβ вычисляется как отношение мнимой и вещественной частей корня (по модулю): μ = |β/α|. Чем больше эта величина, тем слабее затухают колебания, вызванные этими корнями, за 1 период колебаний.

Линии постоянной колебательности – это лучи, выходящие из начала координат. При проектировании систем обычно требуется обеспечить быстродействие не ниже заданного (степень устойчивости не меньше заданной ηmin) и колебательность не выше заданной μmax. Эти условия определяют усеченный сектор на комплексной плоскости, Рис.7.21.

Рис.7.21.Линии постоянной колебательности.

ПИД - регулятор

Среди всего разнообразия регуляторов необходимо выделить отдельный тип – пропорционально-интегрально-дифференциальный регулятор (ПИД-регулятор). В английской терминологии: proportional–integral–derivativecontroller (PIDcontroller). Около 80% регуляторов в промышленности – это ПИД-регуляторы. ПИД-регулятор предназначен для решения задач управления объектами с одним входом и одним выходом.

ПИД-регулятор в современном понимании был предложен и проанализирован в статье Николая Минорского (NicolasMinorsky) в 1922 году. Командование Флота США наняло инженера русского происхождения Николая Минорского для разработки автоматической системы управления движением судна (shipsteeringsystem), которая помогала бы рулевому корабля и автоматически выполняла некоторые его действия. В результате наблюдений было замечено, что рулевой, пытаясь вернуть корабль на заданный курс, поворачивает штурвал судна тем сильнее, чем больше отклонение корабля от курса. Минорский предположил, что можно использовать следующее управляющее воздействие: 𝑢(𝑡) = 𝑘・𝑒(𝑡) где 𝑘>0 – некоторая постоянная. Поскольку управляющее воздействие постоянно связано с отклонением 𝑢(𝑡) = 𝑘・𝑒(𝑡), то при схода корабля с курса произойдет немедленное поворачивание руля для коррекции положения. Такой тип управления называется пропорциональное управление – управляющее воздействие пропорционально ошибке.

Продолжая наблюдения, Минорский установил, что опытный рулевой не только поворачивает штурвал судна исходя из текущей ошибки курса, но также учитывает историю предыдущих ошибок положения корабля и скорости изменения ошибки курса.

Управление кораблем в условиях постоянно присутствующих возмущений (например, бокового течения или ветра) требует следующей техники: если корабль долгое время идет параллельным курсом к проложенному на карте – т.е. ошибка курса не велика для эффективного действия пропорционального управления, но присутствует постоянно, то рулевой поворачивает штурвал в сторону линии курса тем сильнее, чем дольше действовала ошибка. Формализация этого действия приводит к управлению, в котором управляющее воздействие – сумма двух компонентов:

,

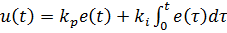где 𝑘𝑝, 𝑘𝑖>0 – некоторые постоянные, выбор которых определяет поведение регулятора. Слагаемое, которое добавляет в управляющее воздействие интеграл от сигнала ошибки, называется интегральным управлением: сигнал ошибки накапливается за все время работы системы и даже небольшая, но продолжительно действующая ошибка, приведет к компенсирующему ее воздействию.

Интегральное управление предназначено для повышения точности управления и позволяет бороться с постоянно действующими ошибками. Известно, что теоретически свести ошибку регулирования к 0 в задаче установки выхода в заданное значение возможно только при применении интегрального управления – пропорциональное управление всегда оставляет ненулевую ошибку.

Проблема применения интегрального управления состоит в том, что в процессе регулирования управляющее воздействие совершает заметные колебания вокруг искомого постоянного значения. Это объясняется тем, что накопленная ошибка в слагаемом 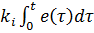обращается в 0, когда сигнал ошибки изменит свой знак и продолжительное время проинтегрируется. В результате возникают продолжительные затухающие колебания управляющей переменной, что нежелательно с точки зрения качества управления.

Для решения этой проблемы в управляющее воздействие добавляют еще один компонент, который подавляет интегральное управление при значительных колебаниях сигнала ошибки, оставляя его действие только на малых и продолжительных ошибках. Этот компонент – дифференциальное управление, которое входит как третье слагаемое:

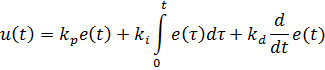
где 𝑘𝑝, 𝑘𝑖, 𝑘𝑑>0 – пропорциональный, интегральный и дифференциальный коэффициент ПИД-регулятора, соответственно.

Управление по производной – это быстрый способ управления. Сигнал дифференциального канала наиболее важен при изменениях входов и исчезает в установившемся режиме. Он позволяет реагировать не на само увеличение ошибки, а на тенденциюее изменения, и принять превентивные меры. Главный недостаток дифференциального канала – большое влияние высокочастотных помех, например, шумов измерений. Для того, чтобы сделать регулятор физически реализуемым, вместо чистого дифференцирования используют инерционное дифференцирующее звено:

,

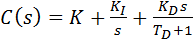где 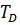– малая постоянная времени. Чем меньше 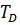, тем в большем частотном диапазоне выполняется точное дифференцирование, но сильнее влияют высокочастотные помехи.

При работе ПИД-регулятора обычно основную часть управляющего воздействия составляет пропорциональный компонент 𝑘𝑝.𝑒(𝑡). Интегральный и дифференциальный компоненты предназначены, в основном, для улучшения точности и качества переходного процесса. Обычно пропорциональный коэффициент выбирают больше остальных: 𝑘𝑝>𝑘𝑖и 𝑘𝑝>𝑘𝑑.

Первое, что существенно важно для практического применения ПИД - регулятора – это коэффициент усиления объекта управления, показывающий,на сколько изменяется выходной сигнал при изменении входного. Если коэффициент усиления положительный –это означает, что увеличение входного сигнала приводит к увеличению выходного. В противном случае – коэффициент усиления отрицательный, Рис.8.1. Для применения ПИД-регулятора необходимо, чтобы коэффициент усиления объекта управления был положительным. Например, если мы занимаемся задачей управления сервоприводом, то положительный коэффициент усиления означает, что подача положительного напряжения приводит к вращению двигателя вперед – к увеличению угловой или линейной координаты.

Рис.8.1. Реакция устойчивой системы с отрицательнымкоэффициентом усиления.

Если коэффициент усиления отрицательный, то выход ПИД-регулятора необходимо соединять с объектом управления через инвертор – элемент, который повторяет сигнал, изменив на противоположный его знак: 𝑢′(𝑡) = −𝑢(𝑡). Кроме собственно ПИД-регулятора в системе управления должен находиться компонент, генерирующий сигнал ошибки:

𝑒(𝑡) =x(𝑡) −𝑦(𝑡). Где𝑦(𝑡) – выход объекта управления, x(𝑡) – вход системы управления, на котором задается желаемое значение на выходе. Отсюда получается структура системы с замкнутой обратной связью, показанная на Рис.8.2, где 𝑃– объект управления с одним входом и выходом, PID – ПИД-регулятор.

Рис.8.2. Система с ПИД регулятором в цепи обратной связи.

Самым простым способом определения параметров ПИД- регулятора может являться следующий. Сначала необходимо обнулить все его коэффициенты 𝑘𝑝= 0, 𝑘𝑖= 0, 𝑘𝑑= 0, что равнозначно отключению ПИД- регулятора от объекта управления. После этого начинают работать с типовым воздействием – ступенькой: на входx(𝑡) в какой-то момент времени подается постоянный сигнал заданной амплитуды x(𝑡) = x*. Надо настроить регулятор так, чтобы сигнал на выходе объекта управления yкак можно лучше и ближе повторял входное воздействие x(𝑡). Для этого постепенно увеличиваем 𝑘𝑝, постоянно проверяя реакцию на ступенчатое воздействие, до тех пор, пока на выходе 𝑦не начнутся колебания – это критическое значение коэффициента 𝑘^max𝑝. После этого необходимо установить окончательное значение коэффициента 𝑘𝑝= 𝑘^max𝑝/2. Качество регулирования можно улучить, подбирая коэффициенты 𝑘𝑖и 𝑘𝑑: если установившаяся ошибка слишком велика, то необходимо немного увеличить 𝑘𝑖; если сильное перерегулирование – увеличить 𝑘𝑑.

Впервые методику расчета параметров ПИД- регулятора предложили Зиглер и Никольс в 1942 году. Эта методика очень проста,но в общем случае не дает оптимальных результатов. Тем не менее, она до сих пор часто используется на практике, хотя с тех пор появилось множество более точных методов.

Основной принцип определения коэффициентов ПИД-регулятора состоит в том, чтобы управляемому объекту дать типовое управляющее воздействие (например, подать постоянный сигнал 𝑢(𝑡) = 1) и посмотреть на его реакцию. Иными словами, определить переходную функцию объекта. Далее по переходной функции по эмпирическим формулам определяютсякоэффициенты регулятора. После расчета параметров регулятораобычнотребуется его ручная подстройка для улучшения качестварегулирования. Для этого используется ряд правил, обоснованных теоретически:

∙ увеличение пропорционального коэффициента увеличивает быстродействие и снижает запас устойчивости,

∙ с уменьшением интегральной составляющей ошибка регулирования с течением времени уменьшается быстрее,

∙ уменьшение постоянной интегрирования уменьшает запас устойчивости,

∙ увеличение дифференциальной составляющей увеличивает запас устойчивости и быстродействие.

Для настройки ПИД-регуляторов можно использовать и общиеметоды теории автоматического управления.Один из методов синтеза регулятора – размещение полюсовпередаточной функции замкнутой системы, которые во многом определяют ее динамику, например, быстродействие и степень затухания колебаний. Смысл в том, чтобы разместить эти полюса в заданных точках комплексной плоскости с помощью специально выбранного регулятора.