Логарифмические частотные характеристики

Частотные характеристики достаточно сложно строить вручную. В 60-е годы, когда развивалась классическая теория управления, не было мощных компьютеров, поэтому наибольшую популярность приобрели приближенные методы, с помощью которых можно было проектировать регуляторы с помощью ручных вычислений и построений. Один из таких подходов основан на использовании логарифмических частотных характеристик.

Вместо A(ω) было предложено использовать логарифмическую амплитудную частотную характеристику (ЛАЧХ): график, на котором по оси абсцисс откладывается десятичный логарифм частоты (lgω), а по оси ординат – величинаL_m(ω) =20lg A(ω), измеряемая в децибелах (дБ). При построении логарифмической фазовой частотной характеристики (ЛФЧХ) по оси абсцисс также откладывается логарифм частоты lgω.

Единицей отсчета на логарифмической оси частот является декада– диапазон, на которомчастота увеличивается в 10 раз (а значение ее логарифма увеличивается на единицу). Вместе ЛАЧХ и ЛФЧХ называются логарифмической амплитудно-фазовой частотной характеристикой (ЛАФЧХ) или диаграммой Боде.

Логарифмические характеристики обладают двумя ценными свойствами:

1) ЛАЧХ и ЛФЧХ для произведения W₁( s) W₂( s) вычисляются как суммы ЛАЧХ и ЛФЧХ отдельных звеньев: 20lgA(ω) = 20lgA₁(ω) + 20lgA₂(ω); φ(ω) =φ₁(ω) +φ₂(ω) ;

2) в области высоких и низких частот ЛАЧХ асимптотически приближаются к прямым, наклон которых составляет ± 20 дБ/дек (децибел на декаду), ± 40 дБ/дек и т.д.

В классической теории управления хорошо разработаны методы анализа и синтеза системна основе асимптотических ЛАЧХ, которые представляют собой ломаные линии и легко строятся вручную.

Рис.5.8. ЛАФЧХ ифазоваяхарактеристикадля звена первого порядка

На Рис.5.8показаны точная (сплошная линия) и асимптотическая (штриховая линия) ЛАФЧХ для звена первого порядка с передаточной функцией

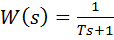при T = 1с.

Первая асимптота, определяющая поведение ЛАЧХ на низких частотах, имеет нулевой наклон, потому что звено относится к классу звеньев, имеющих постоянный ненулевой статический коэффициент усиления, то есть W(0) = 1 ≠ 0 .

Если W(0) = 0 , передаточная функция содержит множитель sk( k >0 ), который соответствует производной порядка k . В этом случае наклон ЛАЧХ на низких частотах равенk ⋅20 дБ/дек.

Если W(0) = ∞, звено содержит один или несколько интеграторов, то есть в знаменателе есть сомножитель sk. Тогда наклон ЛАЧХ на низких частотах равен − k ⋅20 дБ/дек.

Наклон ЛАЧХ на высоких частотахопределяется разностью степеней числителя и знаменателя передаточной функции. Если числитель имеет степень m , а знаменатель – степень n ,то наклон последней асимптоты равен 20⋅(m− n) дБ/дек. В нашем примере m− n = 0 −1 = −1.Поэтому вторая асимптота, определяющая свойства звена на высоких частотах, имеет наклон− 20 дБ/дек, то есть, за одну декаду значение уменьшается на 20 дБ.

Типовые динамические звенья

Обычно система управления состоит из отдельных блоков, каждый из которых описывается уравнениями низкого порядка (чаще всего – первого или второго). Для понимания работы системы в целом желательно хорошо представлять, как ведут себя ее отдельные элементы. Кроме того, при построении ЛАФЧХ сложной системы передаточную функцию разбивают на простейшие сомножители

W( s)= W₁( s) W₂( s) W₃( s)… W_n( s)

и далее, воспользовавшись свойствами ЛАФЧХ, строят характеристики для всей системы как суммы ЛАЧХ и ЛФЧХ отдельных звеньев.

Усилительное звено

Звенья, имеющие конечный ненулевой коэффициент усиления постоянного сигнала, то есть W(0) = k ≠ 0, называются позиционными. Это значит, что числитель и знаменатель передаточной функции имеют ненулевые свободные члены (постоянные слагаемые). Простейшее позиционное звено – идеальный (безынерционный) усилитель. Его передаточная функция W(s) = k . Строго говоря, он не является динамическим звеном, поскольку изменение выхода происходит мгновенно, сразу вслед за изменением входа. При действии на вход единичного ступенчатого сигнала 1(t) (или дельта-функции δ(t) ) на выходе будет такой же сигнал, усиленный в k раз, поэтому переходная и импульсная характеристики звена равны

h(t) = k (t >0) и w(t) = k ⋅δ(t) .

Если на вход усилителя действует синусоидальный сигнал, на выходе он усиливается в kраз без изменения фазы, поэтому амплитудная и фазовая частотная характеристики не зависят от частоты входного сигнала:

A(ω) = k , φ (ω) = 0 .

Апериодическое звено

Одно из самых часто встречающихся звеньев – апериодическое, которое описывается дифференциальным уравнением

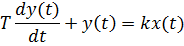
и имеет передаточную функцию 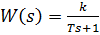. Здесь k – безразмерный коэффициент, а T >0 – постоянная, которая называется постоянной временизвена. Постоянная времени – размерная величина, она измеряется в секундах и характеризует инерционностьобъекта, то есть скорость его реакции на изменение входного сигнала.

Переходная и весовая функции апериодического звена:

,

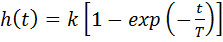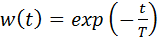
изображены на Рис.6.1.

Рис.6.1.Переходная и импульсная функции апериодического звена.

Предельное значение переходной характеристики равно k , а касательная к ней в точке t = 0 пересекается с линией установившегося значения при t = T. Переходная и импульсная характеристики выходят на установившееся значение (с ошибкой не более 5%) примерно за время 3T. Эти факты позволяют определять постоянную времени экспериментально, по переходной характеристике звена.

Частотная характеристика определяется выражением

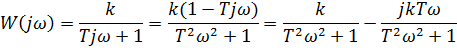
Для каждой частоты ω значение W(jω) – это точка на комплексной плоскости. При изменении ω от 0 до ∞ получается кривая, которая называется годографом Найквиста(диаграммой Найквиста). В данном случае можно показать, что частотная характеристика – это полуокружность с центром в точке (0,5k; 0) радиуса 0,5k . Годограф начинается (на нулевой частоте) вточке (k; 0) и заканчивается в начале координат (приω →∞).

Рис.6.2.Диаграмма Найквиста, ЛАЧХифазоваяхарактеристика апериодического звена.

Асимптотическая ЛАЧХ этого звена образована двумя прямыми, которые пересекаются на сопрягающей частотеω_c = 1/T . На низких частотах она имеет нулевой наклон, причем в этой области L k m ≈ 20lg .

На высоких частотах наклон ЛАЧХ равен − 20 дБ/дек, так как степень знаменателя передаточной функции на единицу больше степени ее числителя. Фазовая характеристика меняется от 0 до − 90°, причем на сопрягающей частоте ω_cона равна − 45°.Поскольку ЛАЧХ уменьшается на высоких частотах, апериодическое звено подавляет высокочастотные шумы, то есть обладает свойством фильтра низких частот.

Для сравнения рассмотрим также неустойчивое апериодическое звено, которое задаетсяуравнением

.

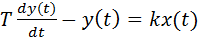Отличие от прежнего уравнения только в знаке в левой части уравнения (плюс сменился на минус). Однако при этом кардинально меняются переходная и импульсная характеристики

, ,

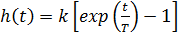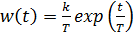изображена на Рис.6.3.

Рис.6.3.Переходная характеристика

неустойчивогоапериодического звена.

Обычно предполагается, что постоянная времени T >0, тогда экспоненты в этих выражениях бесконечно возрастают с ростом t . Поэтому звено названо «неустойчивым»: в покое оно находится в неустойчивом равновесии, а при малейшем возмущении «идет вразнос». Интересно сравнить частотные характеристики устойчивого и неустойчивого апериодических звеньев с теми же коэффициентами усиления и постоянными времени, Рис.6.4.

Рис.6.4. ЛАЧХ ифазоваяхарактеристиканеустойчивого апериодического звена.

Из этого графика видно, что ЛАЧХ неустойчивого звена точно совпадает с ЛАЧХ аналогичного устойчивого, но отрицательный фазовый сдвиг значительно больше. Устойчивое апериодическое звено относится к минимально - фазовым звеньям, то есть его фаза по модулю меньше, чем фаза любого звена с такой же амплитудной характеристикой. Соответственно, неустойчивое звено – неминимально - фазовое.

К неминимально - фазовымзвеньям относятся все звенья, передаточные функции которых имеют нули или полюса в правой полуплоскости, то есть с положительной вещественной частью. Для минимально - фазовыхзвеньев все нули и полюса передаточной функции находятся в левой полуплоскости (имеют отрицательные вещественные части). Например, при положительных постоянных времени T₁, T₂ и T₃ звено с передаточной функцией

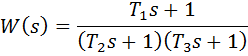
– минимально - фазовое, а звенья с передаточными функциями

, ,

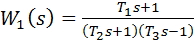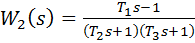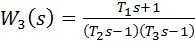
– неминимально - фазовые.

Колебательное звено

Колебательное звено – это звено второго порядка с передаточной функцией вида

,

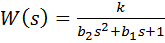знаменатель которой имеет комплексно-сопряженные корни (то есть, b₁²− 4b₂<0). Как известно из теории дифференциальных уравнений, свободное движение такой системы содержит гармонические составляющие (синус, косинус), что дает колебания выхода при изменении входного сигнала.

Передаточную функцию колебательного звенаможно представить в форме

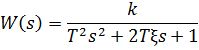
где k – коэффициент, T – постоянная времени (в секундах), ξ – параметр затухания(0 <ξ <1). Постоянная времени определяет инерционность объекта, чем она больше, тем медленнее изменяется выход при изменении входа. Чем больше ξ, тем быстрее затухают колебания.

При ξ = 0 получается консервативноезвено, которое дает незатухающие колебанияна выходе. Если ξ ≥ 1, имеемапериодическое звено второго порядка, то естьпоследовательное соединение двух апериодических звеньев.

Колебательное звено относится к позиционным звеньям, его статический коэффициентусиления равен W(0) = k .Переходная и импульсная характеристики отличаются выраженной колебательностью,особенно при малых значениях параметра затухания ξ. На следующих двух графиках, Рис.6.5,показанылинии, соответствующиеξ = 0,5, иξ = 0,25 .

Рис.6.5. Переходная и импульсная функции колебательного звена.

Асимптотическая ЛАЧХ этого звена, Рис.6.6, образована двумя прямыми, которые пересекаются на сопрягающей частоте c Tω = 1 . На низких частотах прямая имеет нулевой наклон (так как звено позиционное), причем в этой области L k m ≈ 20lg . На высоких частотах наклон ЛАЧХ равен − 40 дБ/дек, так как степень знаменателя передаточной функции на два больше степени ее числителя. Фазовая характеристика меняется от 0 до −180°, причем на сопрягающей частоте ω_cона равна − 90°.

Рис.6.6.ЛАЧХ и фазовая характеристика колебательного звена.

При значениях ξ <0,5 ЛАЧХ имеет «горб» в районе сопрягающей частоты, причем его высота увеличивается с уменьшением ξ. Это означает, что при частоте входного сигнала, равной ω_c наблюдается резонанс, то есть частота возмущения совпадает с частотой собственных колебаний системы. В предельном случае при ξ = 0 (консервативное звено) ЛАЧХ терпит разрыв (обращается в бесконечность) на частоте ω_c, при таком входе амплитуда колебаний неограниченно растет и на практике объект разрушается.

Интегрирующее звено

Простейший пример интегрирующего звена – ванна, в которую набирается вода. Входной сигнал – это поток воды через кран, выход системы – уровень воды в ванне. При поступлении воды уровень растет, система «накапливает» (интегрирует) входной сигнал.

Интегрирующее звено описывается уравнением

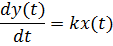
которому соответствует передаточная функция W(s) = k/s.Решение уравнения дает

.

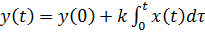Используя это решение для единичного скачка (x(t) = 1 при t ≥ 0) при нулевых начальных условиях (y(0)=0), получаем линейно возрастающую переходную характеристику: h(t) = k ⋅t .

Для того, чтобы найти импульсную характеристику, вспомним, что интеграл от дельта-функции на любом интервале, включающем t = 0 , равен 1. Поэтому w(t) = k (при t ≥ 0 ), Рис.6.7.

Рис.6.7.Переходная и импульсная характеристики интегрирующего звена.

Частотная характеристика интегрирующего звена определяется формулой

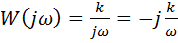.Можно показать, что его логарифмическая амплитудная частотная характеристика – это прямая с наклоном − 20 дБ/дек. На низких частотах усиление максимально, теоретически на частоте ω = 0 оно равно бесконечности. Высокие частоты, наоборот, подавляются интегратором.

Рис.6.8.ЛАЧХ и фазовая характеристика интегрирующего звена.

На частоте ω = 1 значение ЛАЧХ равно 20lg k , а при ω = k ЛАЧХ обращается в нуль, поскольку W( jω) = 1. Фазовая характеристика φ (ω) = −90° – говорит о постоянном сдвиге фазы на всех частотах.

Дифференцирующее звено

Дифференцирующее звено дает на выходе производную входного сигнала. Уравнение идеального дифференцирующего звена 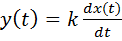,его операторная запись y(t) = k ⋅p x(t) , а передаточная функция W(s) = k ⋅s .

Известно, что производная единичного ступенчатого сигнала 1(t) в точке t = 0 – это дельта-функция δ(t). Поэтому переходная и весовая функции дифференцирующего звена

, .

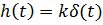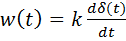Это физически нереализуемые функции, так как дельта-функцию и ее производную, имеющие бесконечные значения, невозможно получить на реальном устройстве. Поэтому идеальное дифференцирующее звено относится к физически нереализуемымзвеньям.

Логарифмическая амплитудная частотная характеристика дифференцирующего звена –прямая с наклоном 20 дБ/дек, пересекающая ось абсцисс L_m(ω) = 0 на частотеω = 1/k . Приω = 1 ЛАЧХ равна L m (1) = 20lgk . Дифференцирующее звено подавляет низкие частоты (производная от постоянного сигнала равна нулю) и бесконечно усиливает высокочастотные сигналы,что требует бесконечной энергии и невозможно в физически реализуемых системах.

Рис.6.8.ЛАЧХ и фазовая характеристика дифференцирующего звена.

Фазовая характеристика не зависит от частоты, звено дает положительный сдвиг фазы на90⁰ . Действительно, при дифференцировании сигнала x(t) = sinωt получаем

.

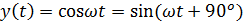Дифференцирующее звено реагирует не на изменение самой входной величины, а на изменение ее производной, то есть на тенденциюразвития событий. Поэтому говорят, что дифференцирующее звено обладает упреждающим, прогнозирующимдействием. С его помощью можно ускорить реакцию системы.

В технике не могут использоваться физически нереализуемые звенья. Поэтому важно рассмотреть аналогичное звено, которое выполняет дифференцирование низкочастотных сигналов и одновременно имеет ограниченное усиление на высоких частотах. Инерционное дифференцирующее звеноописывается уравнением

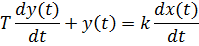
и имеет передаточную функцию 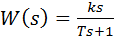. Фактически это последовательное соединение идеального дифференцирующего и апериодического звеньев.

Апериодическое звено добавляет инерционность: обладая свойствами фильтра низких частот, оно ограничивает усиление на высоких частотах. Поскольку передаточная функция имеет равные степени числителя и знаменателя, на высоких частотах (выше сопрягающей чаcтотыωc=1/T) ЛАЧХ имеет нулевой наклон, поэтому неограниченного роста коэффициента усиления не происходит. Одновременно теряется точность дифференцирования, таккак фазовая характеристика изменяется от 90°до нуля, Рис6.9.

Рис.6.9.ЛАЧХ и фазовая характеристика инерционного дифференцирующего звена.

Звено с запаздыванием

Пример системы с запаздыванием – подача нагреваемого воздуха через канал, в котором нагрев воздуха происходит с одной стороны, а измерение температуры – с другой. Очевидно, что при изменении температуры воздуха датчик обнаружит это не сразу, а через время τ = L / v , где L – длина канала метрах, а v – скорость потока воздуха в м/с. В этом случае говорят, что в системе есть транспортное запаздываниена величину τ в секундах, Рис.6.10.

Рис.6.10. Запаздывание выходного сигнала относительно входного.

Другой пример – вычислительное запаздывание в компьютере. Так называется время, которое необходимо для расчета нового управляющего сигнала после получения всех исходных данных. Запаздывание в системе просто сдвигает сигнал вправо на временной оси, не меняя его формы. Математически это можно записать в виде y(t) = x(t −τ) .

Изображение сигнала на выходе звена запаздывания вычисляется по теореме о смещении аргументадля преобразования Лапласа:

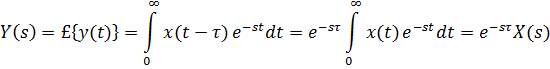
поэтому передаточная функция звена чистого запаздывания равна Wτ(s) = e^-st. Очевидно, что при гармоническом входном сигнале запаздывание не изменяет амплитуду,но вносит дополнительный отрицательный сдвиг фазы. Частотная характеристика этого звена имеет вид Wτ(jω)= e^-jωt. По общим формулам находим:

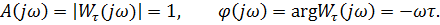
Таким образом, фазовая частотная характеристика звена запаздывания – линейная функция частоты ω, чем больше частота, тем больше фазовый сдвиг.

Анализ систем управления

Каким требованиям должна удовлетворять система управления? Это зависит, прежде всего, от решаемой задачи. В задаче стабилизациинаиболее важны свойства установившегосярежима. Для следящихсистем в первую очередь нужно обеспечить высокое качество переходных процессов при изменении задающего сигнала (уставки).

В целом можно выделить четыре основных требования:

• точность– в установившемся режиме система должна поддерживать заданное значениевыхода системы, причем ошибка (разница между заданным и фактическим значением)не должна превышать допустимую;

• устойчивость– система должна оставаться устойчивой на всех режимах, не должна идти «вразнос» (корабль не должен идти по кругу при смене курса);

• качество переходных процессов– при смене заданного значения система должна переходить в нужное состояние по возможности быстро и плавно;

• робастность– система должна сохранять устойчивость и приемлемое качество даже втом случае, если динамика объекта и свойства внешних возмущений немного отличаются от тех, что использовались при проектировании.

Точность

Точность системы обычно оценивается для одного из эталонных входных сигналов. Это может быть единичный скачок

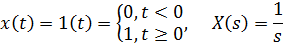
или линейно возрастающий сигнал

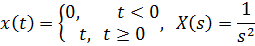
или гармонический сигнал с частотой ω:

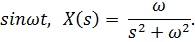
Точность системы в установившемся режиме определяется ошибкой e(t) или ее изображением E(s). Для ее исследования используют передаточную функцию по ошибке W(s) e, которая связывает изображения ошибки и входного сигнала: E(s) = We(s) X(s). Определение точности системы управления подробно рассматривается в [7].

.

Устойчивость

Термин «устойчивость» используется в численных методах, механике, экономике, социологии, психологии. Во всех этих науках имеют в виду, что устойчивая система возвращается в состояние равновесия, если какая-то сила выведет ее из этого состояния. Шарик на рисунке находится в устойчивом равновесии в положении А – если немного сдвинуть его с места, он скатится обратно в ямку, Рис.7.1.

Рис.7.1. Виды равновесия системы.

Однако если шарик сильноотклонить от равновесия, он может свалиться через горку вбок, то есть устойчивость нарушится.

В положениях Б и В шарик также находится в положении равновесия, но оно неустойчиво, так как при малейшем сдвиге в сторону шарик скатывается с вершины.

В положениях Г и Д равновесие шарика нейтральное– при небольшом смещении он остается в новом положении. При этом говорят, что система нейтрально устойчива, то есть находится на границе устойчивости.

• может быть несколько положений равновесия, из них некоторые – устойчивые, а некоторые – нет;

• положение равновесия может быть устойчиво при малых отклонениях (система устойчива «в малом») и неустойчиво при больших («в большом»).

Различают различные виды устойчивости. Устойчивость автономной системы, которую вывели из положения равновесия (задали ненулевые начальные условия) и «отпустили». Система, которая сама возвращается в исходное положение равновесия, называется устойчивой. Если при этом рассматривается только выход системы (а не ее внутреннее состояние), говорят о «технической устойчивости»(или устойчивости по выходу). Напротив, внутренняяили математическая устойчивостьозначает, что не только выход, но и все внутренние переменные (переменные состояния) приближаются к своим значениям в положении равновесия.

В некоторых задачах основной рабочий режим – это периодические колебания, поэтому рассматривается устойчивость процессов, а не только положения равновесия.

На практике обычно важно, чтобы система не «пошла вразнос», то есть, чтобы управляемая величина не росла неограниченно при всех допустимых входных сигналах. Если это так, система обладает устойчивостью «вход-выход»(при ограниченном входе выход также ограничен). При этом нас не интересует, как меняются внутренние переменные объекта, важен только вход и выход.

Техническая устойчивость

В отличие от устойчивости «вход-выход», понятие «техническая устойчивость» относится к автономной системе, у которой все входные сигналы равны нулю. Положением равновесияназывают состояние системы, которая находится в покое, то есть сигнал выхода y(t) – постоянная величина, и все его производные равны нулю. Систему выводят из положения равновесия и убирают все возмущения. Если при этом с течением времени (при t →∞) система возвращается в положение равновесия, она называется устойчивой. Если выходная координата остается ограниченной (не уходит в бесконечность), система называется нейтрально устойчивой, а если выход становится бесконечным – неустойчивой.

Внутренняя устойчивость

Говоря о внутренней устойчивости, рассматривают не только выход, но и все переменные, описывающие состояние системы. В математической теории систем вектор состояния обозначают через x(t), а уравнение движения системы записывают в виде

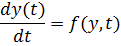
В соответствии с классическим методом решение дифференциального уравнения, описывающего движение рассматриваемой системы, ищется в виде:

y(t) = y_вын(t) + y_св(t).

Здесь y_св(t) - общее решение однородного дифференциального уравнения, то есть уравнения с нулевой правой частью:

a_oy⁽ⁿ⁾ + a₁y^(n-1) + ... + a_(n-1)y’ + a_(n)y = 0.

Физически это означает, что все внешние воздействия сняты и система абсолютно свободна, ее движения определяются лишь собственной структурой. Поэтому решение данного уравнения называется свободной составляющей общего решения. y_вын(t) - частное решение неоднородного дифференциального уравнения, под которым понимается уравнение с ненулевой правой частью. Физически это означает, что к системе приложено внешнее воздействие u(t). Поэтому вторая составляющая общего решения называется вынужденной. Она определяет вынужденный установившийся режим работысистемы после окончания переходного процесса. Можно провести аналогию между системой управления и пружиной, колебания которой описываются аналогичным дифференциальным уравнением (Рис.7.2).

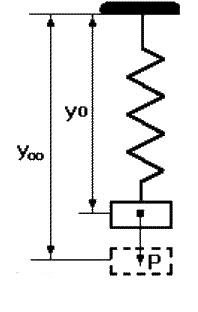
Рис.7.2. Вынужденные колебания пружины

Оттянем пружину, а затем отпустим,предоставив ее самой себе. Пружина будет колебаться в соответствии со свободной составляющей решения уравнения, то есть характер колебаний будет определяться только структурой самой пружины. Если в момент времени t = 0 подвесить к пружине груз, то на свободные колебания наложится внешняя сила Р. После затухания колебаний, описываемых только свободной составляющей общего решения, система перейдет в новый установившийся режим, характеризуемый вынужденной составляющей y_вын = y(t ). Если внешнее воздействие само будет изменяться по синусоидальному закону P = P_osin( t + ), то после затухания переходного процесса система будет совершать вынужденные колебания с той же частотой, что и вынуждающая сила, то есть y_вын = y_maxsin( 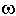t +y).

Можно сказать, что устойчивостьозначает, что все движения x(t), которые начинаются близко от положения равновесия, при всех t остаются в некоторой окрестности положения равновесия. Если система не просто устойчива, а еще и возвращается в положение равновесия, то есть x(t) стремится к равновесному значению при t →∞,в этом случае говорят об асимптотической устойчивости.Например,маятник без трения – устойчивая система, а маятник с трением – асимптотически устойчивая.

Формальное определение внутренней устойчивости было введено в работах А.М. Ляпунова, поэтому такое понятие устойчивости принято называть устойчивостью по Ляпунову.Система первого порядка, с одной переменной состояния x(t), называется устойчивой по Ляпунову в положении равновесия x*, если при начальном отклонении от положения равновесия x* не более, чем на δ, траектория движения отклоняетсяот x* не более, чем на ε, причем для каждого ε можно найти соответствующее ему δ(ε) :

|x₀ – x*| <δ⇒ | x(t) – x*| <ε при всех t > 0 .

Фактически это означает, что чем меньше начальное отклонение, тем меньше траектория движения отклоняется от положения равновесия.

Если кроме того вектор состояния стремится к положению равновесия, то есть | x(t) – x*| → 0 при t → ∞ ,система называется асимптотически устойчивойв положении равновесия x* . Выполнение условия сходимости не гарантирует устойчивость по Ляпунову. Очевидно, что асимптотическая устойчивость – более сильное требование. Положения равновесия, которые устойчивы по Ляпунову, но не асимптотически устойчивы, иногда называются нейтрально устойчивыми(маятник без трения).

Положение равновесия неустойчиво, если для него не выполняется условие устойчивостиЛяпунова. Это значит, что существует такое ε >0 , что траектория x(t) выходит за границы области x(t) − x* <ε при сколь угодно малом отклонении начального состояния x₀от положения равновесия x* . Например, система переходит в другоеположение равновесия, или x(t) неограниченно возрастает.

На Рис.7.3 показаны движения устойчивой, асимптотически устойчивой и неустойчивой систем первого порядка (с одной координатой x(t) ).

Рис.7.3. Движения устойчивой, асимптотически устойчивой и неустойчивой систем.

Траекторию движения систем второго порядка обычно изображают на фазовой плоскости, где по одной оси откладывается x₁(t), а по другой – x₂(t). На следующем рисунке показаны движения устойчивой, асимптотически устойчивой и неустойчивой систем. Для простоты предполагается, что положение равновесия – это начало координат, где x₁ = x₂ = 0.

Рис.7.4. Отображение движения устойчивой, асимптотически устойчивой и неустойчивой систем на фазовой плоскости.

Линейные системы обладают рядом особенностей, которые во многих случаях упрощают анализ устойчивости:

• автономная линейная система (на которую не действуют внешние силы) может иметь единственное положение равновесия (в котором все сигналы равны нулю) или бесконечно много положений равновесия (шарик на плоской поверхности);

• устойчивость – это свойство линейной системы, а не отдельного положения равновесия:

или все ее движения устойчивы (асимптотически устойчивы), или все неустойчивы;

• асимптотическая устойчивость линейной системы «в малом» сразу означает ее устойчивость «в целом», то есть при любых отклонениях от положения равновесия;

• асимптотически устойчивая система также обладает устойчивостью «вход-выход», а просто устойчивая (нейтрально устойчивая, не асимптотически устойчивая) – нет.

Каждая составляющая общего решения уравнения динамики ищется отдельно. Вынужденная составляющая ищется на основе решения уравнения статики для данной системы для времени t 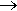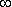. Свободная составляющая представляет собой сумму из nотдельных составляющих:

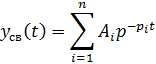
где p_i-корни характеристического уравнения

D(p) = a₀p_n + a₁p_n-1 + a₂p_n-2 + ... + a_n = 0.

Корни могут быть либо вещественными p_i = a_i, либо попарно комплексно сопряженными p_i = a_i ± j i. Постоянные интегрирования А_i определяются исходя из начальных и конечных условий, подставляя в общее решение значения u, y и их производные в моменты времениt = 0 иt .

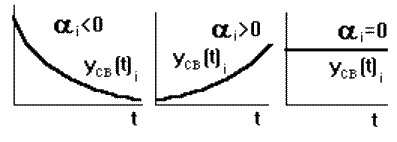
Рис.7.5.Знаки корней характеристического уравнения и устойчивость систем.

Каждому отрицательному вещественному корню соответствует экспоненциально затухающая во времени составляющая y_св(t)_i, каждому положительному - экспоненциально расходящаяся, каждому нулевому корню соответствует y_св(t)_i = const (Рис.7.5). Пара комплексно сопряженных корней с отрицательной вещественной частью определяет затухающие колебания с частотой _i, при положительной вещественной части - расходящиеся колебания, при нулевой - незатухающие (Рис.7.6).

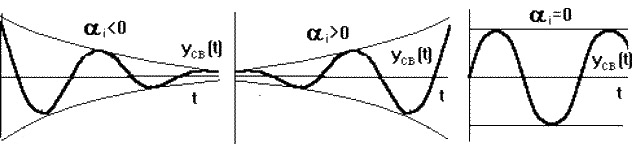
Рис.7.6.Знаки корней характеристического уравнения и характер колебаний системы.

Так как после снятия возмущения y_вын(t) = 0, то устойчивость системы определяется только характером свободной составляющей y_св(t). Поэтому условие устойчивости систем по Ляпунову формулируется так: в устойчивой системе свободная составляющая решения уравнения динамики, записанному в отклонениях, должна стремиться к нулю, то есть затухать.

Рис.7.7.Расположение корней характеристического уравнения на комплексной плоскости и области устойчивости системы.

Исходя из расположения на комплексной плоскости корни с отрицательными вещественными частями называютсялевыми, с положительными - правыми. Поэтому условие устойчивости линейной САУ можно сформулировать следующим образом: для того, чтобы система была устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения были левыми. Если хотя бы один корень правый, то система неустойчива. Если один из корней равен нулю (в системах, где a_n = 0), а остальные левые, то система находится на границе апериодической устойчивости. Если равны нулю вещественные части одной или нескольких пар комплексно сопряженных корней, то система находится на границеколебательной устойчивости.

Правила, позволяющие судить о знаках корней характеристического уравнения без его решения, называются критериями устойчивости. Их можно разделить на алгебраические (основаны на составлении по данному характеристическому уравнению по определенным правилам алгебраических выражений, по которым можно судить об устойчивости систем управления) и частотные (основаны на исследовании частотных характеристик).