Основы теории систем автоматического управления

Принцип обратной связи

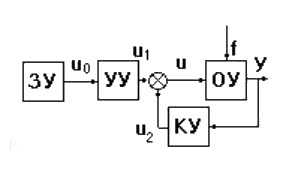
Рис.2.5 Система управления с обратной связью

Наибольшее распространение в технике получил принцип обратной связи,Рис.2.5. Здесь управляющее воздействие корректируется в зависимости от выходной величины y(t). Не важно, какие возмущения действуют на объект управления. Если значение y(t) отклоняется от требуемого, то происходит корректировка сигнала u(t) с целью уменьшения данного отклонения. Связь выхода объекта управления с его входом называется главнойобратной связью (ОС).

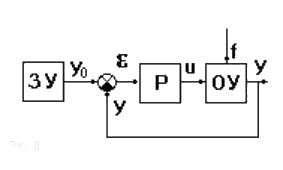
Рис.2.6 Система управления с обратной связью

В частном случае (Рис.2.6) задающее устройство (ЗУ) формирует требуемое значение выходной величины y_о(t), которое сравнивается с действительным значением на выходе САУ y(t). Отклонение ε = y_о-y с выхода сравнивающего устройства подается на вход регулятораР, объединяющего в себе чувствительный элемент, управляющий органобъектаи управляющее устройство. Если ε 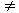0, то регулятор формирует управляющее воздействие u(t), действующее до тех пор, пока не обеспечится равенство ε = 0, или y = y_о. Так как на регулятор подается разность сигналов, то такая обратная связь называется отрицательной, в отличие от положительной обратной связи, когда сигналыскладываются.

Замкнутые системы для своей работы используют текущую рабочую информацию о выходных величинах, определяют отклонение регулируемой величины от заданного значения и принимают меры для устранения этого отклонения.

Такое управление функцией отклонения называется регулированием, а подобную САУ называют системой автоматического регулирования (САР). На Рис.2.7изображена упрощенная схема САР хлебопекарной печи. Роль задающего устройства здесь выполняет потенциометр, напряжение на котором Uз сравнивается с напряжением на термопаре Uт. Их разность 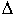U через усилитель подается на исполнительный двигатель ИД, регулирующий через редуктор положение движка реостата в цепи НЭ. Наличие усилителя говорит о том, что данная САР является системой непрямого регулирования, так как энергия для функций управления берется от посторонних источников питания, в отличие от систем прямого регулирования, в которых энергия берется непосредственно от ОУ, как, например, в САР уровня воды в баке Рис.2.8. Недостатком принципа обратной связи является инерционность системы. Поэтому часто применяют комбинацию данного принципа с принципом компенсации, что позволяет объединить достоинства обоих принципов: быстроту реакции на возмущение принципа компенсации и точность регулирования независимо от природы возмущений принципа обратной связи.

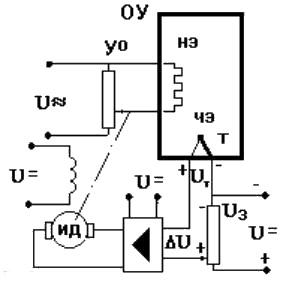
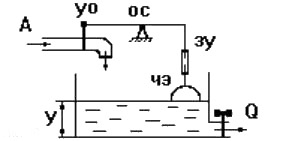
Рис.2.7. Схема автоматического регулирования Рис.2.8 Регулирование уровня воды в баке

печи

Статические характеристики

Режимработы системы управления, в котором управляемая величина и все промежуточные величины не изменяются во времени, называется установившимся, или статическим режимом.

Любое звено и система управления в целом в данном режиме описывается уравнениями статики вида y = F(u,f), в которых отсутствует время t. Соответствующие им графики называются статическими характеристиками. Статическая характеристика звена с одним входом u может быть представлена кривой y = F(u),Рис.3.1. Если звено имеет второй вход по возмущениюf, то статическая характеристика задается семейством кривых y = F(u) при различных значенияхf, или y = F(f) при различных u.

Рис.3.1. Статические характеристики САУ без возмущения и при наличии возмущения

Рис.3.2. Механический аналог системы регулирования воды

Механическим аналогом системы регулирования воды в баке является обычный рычаг Рис.3.2. Уравнение статики для него имеет вид y = Ku. Его можно изобразить звеном, функцией которого является усиление (или ослабление) входного сигнала в K раз. КоэффициентK = y/u, равный отношению выходной величины к входной называется коэффициентом усиления звена. Когда входная и выходная величины имеют разную природу, его называют коэффициентом передачи.

Рис.3.3. Статическая характеристика звена

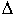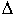Статическая характеристика данного звена имеет вид отрезка прямой линии с наклоном α = arctg(L₂/L₁) = arctg(K)Рис.3.3. Звенья с линейными статическими характеристиками называются линейными. Статические характеристики реальных звеньев, как правило, нелинейны. Такие звенья называются нелинейными. Для них характерна зависимость коэффициента передачи от величины входного сигнала:K = y/ u 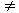const. Например, статическая характеристика насыщенного генератора постоянного тока представлена на Рис.3.4. Обычно нелинейная характеристика не может быть выражена какой-либо математической зависимостью и ее приходится задавать таблично или графически.

Рис.3.4. Статическая характеристика насыщенного генератора постоянного тока

Зная статические характеристики отдельных звеньев, можно построить статическую характеристику САУ. Если все звенья САУ линейные, то САУ имеет линейную статическую характеристику и называется линейной. Если хотя бы одно звено нелинейное, то вся САУ нелинейная.

Звенья, для которых можно задать статическую характеристику в виде жесткой функциональной зависимости выходной величины от входной, называются статическими. Если такая связь отсутствует и каждому значению входной величины соответствует множество значений выходной величины, то такое звено называется астатическим. Изображать его статическую характеристику бессмысленно. Примером астатического звена может служить двигатель, входной величиной которого является напряжение U, а выходной – угол поворота валаα, величина которого при U = const может принимать любые значения. Выходная величина астатического звена даже в установившемся режиме является функцией времени.

Передаточная функция

В теории автоматического управления часто используют операторную форму записи дифференциальных уравнений. При этом вводится понятие дифференциального оператораp = d/dt так что dy/dt = py, а pⁿ = dⁿ/dtⁿ. Это лишь другое обозначение операции дифференцирования. Обратная дифференцированию операция интегрирования записывается как 1/p. В операторной форме исходное дифференциальное уравнение записывается как алгебраическое:

a_op⁽ⁿ⁾y + a₁p^(n-1)y + ... + a_ny = (a_op⁽ⁿ⁾ + a₁p^(n-1) + ... + a_n)y = (b_op^(m) + b₁p^(m-1) + ...+bm)u

Не надо путать эту форму записи с операционным исчислением хотя бы потому, что здесь используются непосредственно функции времени y(t), u(t) (оригиналы), а не их изображенияY(p), U(p), получаемые из оригиналов по формуле преобразования Лапласа. Вместе с тем при нулевых начальных условиях с точностью до обозначений записи действительно очень похожи. Это сходство лежит в природе дифференциальных уравнений. Поэтому некоторые правила операционного исчисления применимы к операторной форме записи уравнения динамики. Так оператор p можно рассматривать в качестве сомножителя без права перестановки, то есть py 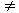yp. Его можно выносить за скобки и т.п.

Поэтому уравнение динамики можно записать также в виде:

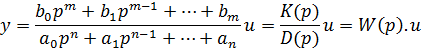
Дифференциальный оператор W(p) называют передаточной функцией. Она определяет отношение выходной величины звена квходной в каждый момент времени: W(p) = y(t)/u(t), поэтому ее еще называют динамическим коэффициентом усиления. В установившемся режиме d/dt = 0, то есть p = 0, поэтому передаточная функция превращается в коэффициент передачи звена K = b_m/a_n.

Знаменатель передаточной функции D(p) = a_opⁿ + a₁p^{n - 1} + a₂p^{n - 2} + ... + a_n называют характеристическим полиномом. Его корни, то есть значения p, при которых знаменатель D(p) обращается в ноль, а W(p) стремится к бесконечности, называются полюсами передаточной функции.

Числитель K(p) = b_op^m + b₁p^{m – 1}+ ... + b_m называют операторным коэффициентом передачи. Его корни, при которых K(p) = 0 и W(p) = 0, называются нулями передаточной функции.

Звено системы управления с известной передаточной функцией называется динамическим звеном. Оно изображается прямоугольником, внутри которого записывается выражение передаточной функции. То есть это обычное функциональное звено, функция которого задана математической зависимостью выходной величины от входной в динамическом режиме. Для звена с двумя входами и одним выходом должны быть записаны две передаточные функции по каждому из входов. Передаточная функция является основной характеристикой звена в динамическом режиме, из которой можно получить все остальные характеристики. Она определяется только параметрами системы и не зависит от входных и выходных величин. Например, одним из динамических звеньев является интегратор. Его передаточная функция W_и(p) = 1/p. Схема САУ, составленная из динамических звеньев, называется структурной.

5. Элементарные динамические звенья

Динамика большинства функциональных элементов САУ независимо от исполнения может быть описана одинаковыми по форме дифференциальными уравнениями не более второго порядка. Такие элементы называют элементарными динамическими звеньями. Передаточная функция элементарного звена в общем виде задается отношением двух полиномов не более чем второй степени

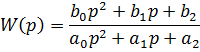
Известно также, что любой полином произвольного порядка можно разложить на простые сомножители не более, чем второго порядка. Так по теореме Виета можно записать

D(p) = a_opⁿ + a₁p^{n - 1} + a₂p^{n - 2} + ... + a_n = a_o(p - p₁)(p - p₂)...(p - p_n),

где p₁, p2, ..., p_n - корни полинома D(p). Аналогично

K(p) = b_opm + b₁p^{m - 1}+ ... + bm = b_o(p - p^~₁)(p - p^~₂)...(p - p^~m),

где p^~₁, p^~₂, ..., p^~m - корни полинома K(p). То есть

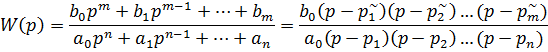
Корни любого полинома могут быть либо вещественными p_i = a_i, либо комплексными попарно сопряженными p_i = a_i ± j 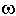_i . Любому вещественному корню при разложении полинома соответствует сомножитель (p - a_i ). Любая пара комплексно сопряженных корней соответствует полиному второй степени, так как

(p - a_i + j 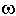_i )(p - a_i - j 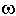_i ) = (p - ai)² + 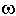_i² = p² - 2pa_i + (a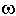_i² + _i²).

То есть

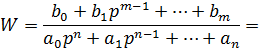
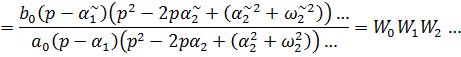
Поэтому любую сложную передаточную функцию линеаризованной системы управления можно представить как произведение передаточных функций элементарных звеньев. Каждому такому звену в реальной системе управления, как правило, соответствует какой - то отдельный узел. Зная свойства отдельных звеньев можно судить о динамики САУ в целом.В теории удобно ограничиться рассмотрением типовых звеньев, передаточные функции которых имеют числитель или знаменатель, равный единице, то есть

,

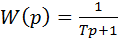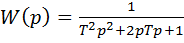
W(p) = 1/p, W(p) = p, W(p) = Tp + 1, W(p) = k.

Из них могут быть образованы все остальные звенья. Звенья, у которых порядок полинома числителя больше порядка полинома знаменателя, технически нереализуемы.

Переходная функция

Часто для изучения реакции объекта управления вместе с управляющей системой на внешнее возмущение в качестве такого возмущения используется некоторый стандартный сигнал. Один из простейших сигналов – так называемый «единичный скачок» («единичный ступенчатый сигнал»), то есть мгновенное изменение входного сигнала с 0 до 1 в момент t = 0 . Формально этот сигнал определяется так:

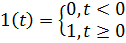
Реакция объекта на единичный скачок называется переходной функциейи обозначается h(t), что показано на Рис.5.1.

Рис.5.1. Единичный скачок и реакция системы на него

При этом предполагается, что объект в начальный момент находится в состоянии покоя, то есть имеет нулевые начальные условия. Это значит, что все его переменные состояния равны нулю и внутренняя энергия также нулевая.

Если начальные условия ненулевые, то для построения сигнала выхода при любом входе нужно использовать дифференциальные уравнения объекта или модель в пространстве состояний. Это значит, что переходная характеристика дает меньше информации, чем исходные уравнения.

Пусть модель объекта задана дифференциальным уравнением первого порядка:

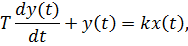
где k – безразмерный коэффициент, а T – некоторая постоянная, которая имеет размерностьвремени (измеряется в секундах). Найдем переходную характеристику этого звена. Решая уравнение при x(t) = 1 ( t>0 ), получаем

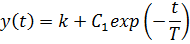
где постоянная C₁должна определяться из начальных условий. Поскольку нас интересует переходная характеристика, начальные условия считаем нулевыми, то есть y(0) = 0, что дает C₁= −k и поэтому

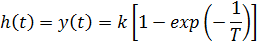
На Рис.5.2 показаны переходные характеристики при различных значениях параметра T, который называется постоянной временизвена:

Рис.5.2.Переходные характеристики в зависимости от постоянной времени

Видно, что при увеличении Tвыход yмедленнее достигает установившегося значения, равного k, то есть постоянная времени характеризует инерционностьзвена. Чем больше постоянная времени, тем медленнее реагирует объект на управление и тем больше усилий нужно длятого, чтобы перевести его в новое состояние. Ступенчатый сигнал легко получить на практике, поэтому переходную характеристику можно снять экспериментально.

Частотные характеристики

Еще один стандартный эталонный сигнал – гармонический (синус, косинус), например: x(t) = sinωt, где ω– угловая частота (в радианах в секунду). Можно показать, что при таком входе на выходе линейной системы в установившемся режиме (при больших t) будет синус той же частоты, но с другой амплитудой A и сдвигом фазы φ:

y(t) = A(ω) ⋅sin(ωt +φ(ω)) .

Для каждой частоты входного сигнала будет своя амплитуда и свой сдвиг фазы. Чтобы определить по графику фазовый сдвиг φ, нужно найти расстояние Δtпо оси времени между соответствующими точками синусоид (например, точками пересечения с осью t или вершинами). Если Δtумножить на частоту ω, получаем сдвиг фазы φ(в радианах).

На Рис.5.5 показан случай φ>0 (опережение по фазе), когда выход сдвинут «влево» по оси времени относительно входа, то есть, «идет раньше» входного.

Рис.5.5. Сдвиг выходного сигнала по фазе.

Зная передаточную функцию системы W(s) , можно вычислить амплитуду и сдвиг фазы по формулам

, .

Запись W(jω) означает, что в передаточную функцию W(s) подставляется чисто мнимое число s = jω, где j= −1 . Для каждой частоты ωзначение W(jω) = P + jQ– это некоторое комплексное число, имеющее амплитуду W(jω)= P2 +Q2 и фазу argW( jω) = arctg(Q/P) .

Функция W(jω) называется частотной характеристикойзвена, поскольку она характеризует выход системы при гармонических сигналах разной частоты. Зависимости P(ω) и Q(ω)(вещественная и мнимая части W( jω) ) – это вещественная и мнимая частотные характеристики.

Функции A(ω) иφ(ω) (они для каждой частоты принимают вещественные значения) называются соответственно амплитуднойи фазовой частотными характеристиками(АЧХ иФЧХ).Амплитудная частотная характеристика – это коэффициент усиления гармоническогосигнала. Если на какой-то частоте ωзначениеA(ω) >1, входной сигнал усиливается, еслиA(ω) <1, то вход данной частоты ослабляется.

По форме АЧХ различают несколько основных типов звеньев:

1) фильтр низких частот– пропускает низкочастотные сигналы примерно с одинаковымкоэффициентом усиления, блокирует высокочастотные шумы и помехи;

2) фильтр высоких частот– пропускает высокочастотные сигналы, блокирует сигналынизкой частоты;

3) полосовой фильтр– пропускает только сигналы с частотами в полосе от ω₁до ω₂;

4) полосовой режекторный фильтр– блокирует только сигналы с частотами в полосе отω₁до ω₂, остальные пропускает.

На Рис.5.6 показаны амплитудные частотные характеристики идеальных фильтров этих четырех типов:

Рис.5.6.Амплитудные частотные характеристики идеальных фильтров.

В радиотехнике используется понятие полосы пропускания– это ширина полосы частот, в которой значение АЧХ больше чем 1/2 от ее максимального значения.

Частотные характеристики во многих случаях можно снять экспериментально. Если объект устойчивый, на его вход подается гармонический сигнал и записывается сигнал y(t) на выходе. Определив амплитуду и сдвиг фазы для разных частот, можно построить по точкам амплитудную и фазовую частотные характеристики,Рис.5.7.

Рис.5.7. Определение амплитудной и фазовой частотных характеристик.

Если объект неустойчив, то при подаче на вход синуса амплитуда колебаний на выходебудет неограниченно расти. Однако частотную характеристику все равно можно определитьэкспериментально. Для этого нужно подключить какой-нибудь регулятор, который сделаетзамкнутую систему устойчивой. Затем на вход r(t) подают синусоидальный сигнал и сравнивают сигналы x(t) и y(t) на входе и выходе интересующего нас объекта, определяя для каждойчастоты ω«коэффициент усиления» A(ω) (отношение амплитуд сигналов x(t) и y(t) ) и сдвигфазыφ(ω)

Типовые динамические звенья

Обычно система управления состоит из отдельных блоков, каждый из которых описывается уравнениями низкого порядка (чаще всего – первого или второго). Для понимания работы системы в целом желательно хорошо представлять, как ведут себя ее отдельные элементы. Кроме того, при построении ЛАФЧХ сложной системы передаточную функцию разбивают на простейшие сомножители

W( s)= W₁( s) W₂( s) W₃( s)… W_n( s)

и далее, воспользовавшись свойствами ЛАФЧХ, строят характеристики для всей системы как суммы ЛАЧХ и ЛФЧХ отдельных звеньев.

Усилительное звено

Звенья, имеющие конечный ненулевой коэффициент усиления постоянного сигнала, то есть W(0) = k ≠ 0, называются позиционными. Это значит, что числитель и знаменатель передаточной функции имеют ненулевые свободные члены (постоянные слагаемые). Простейшее позиционное звено – идеальный (безынерционный) усилитель. Его передаточная функция W(s) = k . Строго говоря, он не является динамическим звеном, поскольку изменение выхода происходит мгновенно, сразу вслед за изменением входа. При действии на вход единичного ступенчатого сигнала 1(t) (или дельта-функции δ(t) ) на выходе будет такой же сигнал, усиленный в k раз, поэтому переходная и импульсная характеристики звена равны

h(t) = k (t >0) и w(t) = k ⋅δ(t) .

Если на вход усилителя действует синусоидальный сигнал, на выходе он усиливается в kраз без изменения фазы, поэтому амплитудная и фазовая частотная характеристики не зависят от частоты входного сигнала:

A(ω) = k , φ (ω) = 0 .

Апериодическое звено

Одно из самых часто встречающихся звеньев – апериодическое, которое описывается дифференциальным уравнением

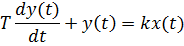
и имеет передаточную функцию 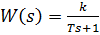. Здесь k – безразмерный коэффициент, а T >0 – постоянная, которая называется постоянной временизвена. Постоянная времени – размерная величина, она измеряется в секундах и характеризует инерционностьобъекта, то есть скорость его реакции на изменение входного сигнала.

Переходная и весовая функции апериодического звена:

,

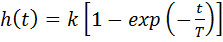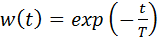
изображены на Рис.6.1.

Рис.6.1.Переходная и импульсная функции апериодического звена.

Предельное значение переходной характеристики равно k , а касательная к ней в точке t = 0 пересекается с линией установившегося значения при t = T. Переходная и импульсная характеристики выходят на установившееся значение (с ошибкой не более 5%) примерно за время 3T. Эти факты позволяют определять постоянную времени экспериментально, по переходной характеристике звена.

Частотная характеристика определяется выражением

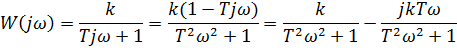
Для каждой частоты ω значение W(jω) – это точка на комплексной плоскости. При изменении ω от 0 до ∞ получается кривая, которая называется годографом Найквиста(диаграммой Найквиста). В данном случае можно показать, что частотная характеристика – это полуокружность с центром в точке (0,5k; 0) радиуса 0,5k . Годограф начинается (на нулевой частоте) вточке (k; 0) и заканчивается в начале координат (приω →∞).

Рис.6.2.Диаграмма Найквиста, ЛАЧХифазоваяхарактеристика апериодического звена.

Асимптотическая ЛАЧХ этого звена образована двумя прямыми, которые пересекаются на сопрягающей частотеω_c = 1/T . На низких частотах она имеет нулевой наклон, причем в этой области L k m ≈ 20lg .

На высоких частотах наклон ЛАЧХ равен − 20 дБ/дек, так как степень знаменателя передаточной функции на единицу больше степени ее числителя. Фазовая характеристика меняется от 0 до − 90°, причем на сопрягающей частоте ω_cона равна − 45°.Поскольку ЛАЧХ уменьшается на высоких частотах, апериодическое звено подавляет высокочастотные шумы, то есть обладает свойством фильтра низких частот.

Для сравнения рассмотрим также неустойчивое апериодическое звено, которое задаетсяуравнением

.

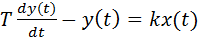Отличие от прежнего уравнения только в знаке в левой части уравнения (плюс сменился на минус). Однако при этом кардинально меняются переходная и импульсная характеристики

, ,

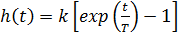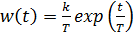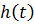изображена на Рис.6.3.

Рис.6.3.Переходная характеристика

неустойчивогоапериодического звена.

Обычно предполагается, что постоянная времени T >0, тогда экспоненты в этих выражениях бесконечно возрастают с ростом t . Поэтому звено названо «неустойчивым»: в покое оно находится в неустойчивом равновесии, а при малейшем возмущении «идет вразнос». Интересно сравнить частотные характеристики устойчивого и неустойчивого апериодических звеньев с теми же коэффициентами усиления и постоянными времени, Рис.6.4.

Рис.6.4. ЛАЧХ ифазоваяхарактеристиканеустойчивого апериодического звена.

Из этого графика видно, что ЛАЧХ неустойчивого звена точно совпадает с ЛАЧХ аналогичного устойчивого, но отрицательный фазовый сдвиг значительно больше. Устойчивое апериодическое звено относится к минимально - фазовым звеньям, то есть его фаза по модулю меньше, чем фаза любого звена с такой же амплитудной характеристикой. Соответственно, неустойчивое звено – неминимально - фазовое.

К неминимально - фазовымзвеньям относятся все звенья, передаточные функции которых имеют нули или полюса в правой полуплоскости, то есть с положительной вещественной частью. Для минимально - фазовыхзвеньев все нули и полюса передаточной функции находятся в левой полуплоскости (имеют отрицательные вещественные части). Например, при положительных постоянных времени T₁, T₂ и T₃ звено с передаточной функцией

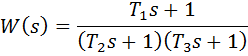
– минимально - фазовое, а звенья с передаточными функциями

, ,

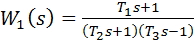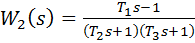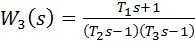
– неминимально - фазовые.

Колебательное звено

Колебательное звено – это звено второго порядка с передаточной функцией вида

,

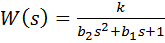знаменатель которой имеет комплексно-сопряженные корни (то есть, b₁²− 4b₂<0). Как известно из теории дифференциальных уравнений, свободное движение такой системы содержит гармонические составляющие (синус, косинус), что дает колебания выхода при изменении входного сигнала.

Передаточную функцию колебательного звенаможно представить в форме

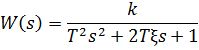
где k – коэффициент, T – постоянная времени (в секундах), ξ – параметр затухания(0 <ξ <1). Постоянная времени определяет инерционность объекта, чем она больше, тем медленнее изменяется выход при изменении входа. Чем больше ξ, тем быстрее затухают колебания.

При ξ = 0 получается консервативноезвено, которое дает незатухающие колебанияна выходе. Если ξ ≥ 1, имеемапериодическое звено второго порядка, то естьпоследовательное соединение двух апериодических звеньев.

Колебательное звено относится к позиционным звеньям, его статический коэффициентусиления равен W(0) = k .Переходная и импульсная характеристики отличаются выраженной колебательностью,особенно при малых значениях параметра затухания ξ. На следующих двух графиках, Рис.6.5,показанылинии, соответствующиеξ = 0,5, иξ = 0,25 .

Рис.6.5. Переходная и импульсная функции колебательного звена.

Асимптотическая ЛАЧХ этого звена, Рис.6.6, образована двумя прямыми, которые пересекаются на сопрягающей частоте c Tω = 1 . На низких частотах прямая имеет нулевой наклон (так как звено позиционное), причем в этой области L k m ≈ 20lg . На высоких частотах наклон ЛАЧХ равен − 40 дБ/дек, так как степень знаменателя передаточной функции на два больше степени ее числителя. Фазовая характеристика меняется от 0 до −180°, причем на сопрягающей частоте ω_cона равна − 90°.

Рис.6.6.ЛАЧХ и фазовая характеристика колебательного звена.

При значениях ξ <0,5 ЛАЧХ имеет «горб» в районе сопрягающей частоты, причем его высота увеличивается с уменьшением ξ. Это означает, что при частоте входного сигнала, равной ω_c наблюдается резонанс, то есть частота возмущения совпадает с частотой собственных колебаний системы. В предельном случае при ξ = 0 (консервативное звено) ЛАЧХ терпит разрыв (обращается в бесконечность) на частоте ω_c, при таком входе амплитуда колебаний неограниченно растет и на практике объект разрушается.

Интегрирующее звено

Простейший пример интегрирующего звена – ванна, в которую набирается вода. Входной сигнал – это поток воды через кран, выход системы – уровень воды в ванне. При поступлении воды уровень растет, система «накапливает» (интегрирует) входной сигнал.

Интегрирующее звено описывается уравнением

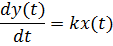
которому соответствует передаточная функция W(s) = k/s.Решение уравнения дает

.

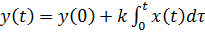Используя это решение для единичного скачка (x(t) = 1 при t ≥ 0) при нулевых начальных условиях (y(0)=0), получаем линейно возрастающую переходную характеристику: h(t) = k ⋅t .

Для того, чтобы найти импульсную характеристику, вспомним, что интеграл от дельта-функции на любом интервале, включающем t = 0 , равен 1. Поэтому w(t) = k (при t ≥ 0 ), Рис.6.7.

Рис.6.7.Переходная и импульсная характеристики интегрирующего звена.

Частотная характеристика интегрирующего звена определяется формулой

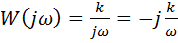.Можно показать, что его логарифмическая амплитудная частотная характеристика – это прямая с наклоном − 20 дБ/дек. На низких частотах усиление максимально, теоретически на частоте ω = 0 оно равно бесконечности. Высокие частоты, наоборот, подавляются интегратором.

Рис.6.8.ЛАЧХ и фазовая характеристика интегрирующего звена.

На частоте ω = 1 значение ЛАЧХ равно 20lg k , а при ω = k ЛАЧХ обращается в нуль, поскольку W( jω) = 1. Фазовая характеристика φ (ω) = −90° – говорит о постоянном сдвиге фазы на всех частотах.

Дифференцирующее звено

Дифференцирующее звено дает на выходе производную входного сигнала. Уравнение идеального дифференцирующего звена 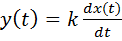,его операторная запись y(t) = k ⋅p x(t) , а передаточная функция W(s) = k ⋅s .

Известно, что производная единичного ступенчатого сигнала 1(t) в точке t = 0 – это дельта-функция δ(t). Поэтому переходная и весовая функции дифференцирующего звена

, .

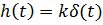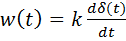Это физически нереализуемые функции, так как дельта-функцию и ее производную, имеющие бесконечные значения, невозможно получить на реальном устройстве. Поэтому идеальное дифференцирующее звено относится к физически нереализуемымзвеньям.

Логарифмическая амплитудная частотная характеристика дифференцирующего звена –прямая с наклоном 20 дБ/дек, пересекающая ось абсцисс L_m(ω) = 0 на частотеω = 1/k . Приω = 1 ЛАЧХ равна L m (1) = 20lgk . Дифференцирующее звено подавляет низкие частоты (производная от постоянного сигнала равна нулю) и бесконечно усиливает высокочастотные сигналы,что требует бесконечной энергии и невозможно в физически реализуемых системах.

Рис.6.8.ЛАЧХ и фазовая характеристика дифференцирующего звена.

Фазовая характеристика не зависит от частоты, звено дает положительный сдвиг фазы на90⁰ . Действительно, при дифференцировании сигнала x(t) = sinωt получаем

.

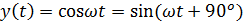Дифференцирующее звено реагирует не на изменение самой входной величины, а на изменение ее производной, то есть на тенденциюразвития событий. Поэтому говорят, что дифференцирующее звено обладает упреждающим, прогнозирующимдействием. С его помощью можно ускорить реакцию системы.

В технике не могут использоваться физически нереализуемые звенья. Поэтому важно рассмотреть аналогичное звено, которое выполняет дифференцирование низкочастотных сигналов и одновременно имеет ограниченное усиление на высоких частотах. Инерционное дифференцирующее звеноописывается уравнением

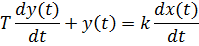
и имеет передаточную функцию 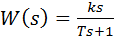. Фактически это последовательное соединение идеального дифференцирующего и апериодического звеньев.

Апериодическое звено добавляет инерционность: обладая свойствами фильтра низких частот, оно ограничивает усиление на высоких частотах. Поскольку передаточная функция имеет равные степени числителя и знаменателя, на высоких частотах (выше сопрягающей чаcтотыωc=1/T) ЛАЧХ имеет нулевой наклон, поэтому неограниченного роста коэффициента усиления не происходит. Одновременно теряется точность дифференцирования, таккак фазовая характеристика изменяется от 90°до нуля, Рис6.9.

Рис.6.9.ЛАЧХ и фазовая характеристика инерционного дифференцирующего звена.

Звено с запаздыванием

Пример системы с запаздыванием – подача нагреваемого воздуха через канал, в котором нагрев воздуха происходит с одной стороны, а измерение температуры – с другой. Очевидно, что при изменении температуры воздуха датчик обнаружит это не сразу, а через время τ = L / v , где L – длина канала метрах, а v – скорость потока воздуха в м/с. В этом случае говорят, что в системе есть транспортное запаздываниена величину τ в секундах, Рис.6.10.

Рис.6.10. Запаздывание выходного сигнала относительно входного.

Другой пример – вычислительное запаздывание в компьютере. Так называется время, которое необходимо для расчета нового управляющего сигнала после получения всех исходных данных. Запаздывание в системе просто сдвигает сигнал вправо на временной оси, не меняя его формы. Математически это можно записать в виде y(t) = x(t −τ) .

Изображение сигнала на выходе звена запаздывания вычисляется по теореме о смещении аргументадля преобразования Лапласа:

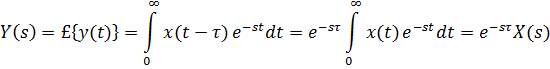
поэтому передаточная функция звена чистого запаздывания ра