Алфавитный подход к измерению информации

Как можно измерить количество информации? Да также, как мы измеряем длину или массу чего-нибудь: сравнить с соответствующим эталоном. Сколько раз эталонная единица укладывается в измеряемой величине, таков и результат измерения. Надо только выбрать эталон.

Например, в мультфильме «38 попугаев» эталоном длины служит длина шага попугая.

Каков же эталон для измерения информации? Давайте в этом разберемся.

Существует несколько способов измерения количества информации. Один из них называется алфавитный.

Алфавитный подход позволяет измерять количество информации в тексте (символьном сообщении), составленном из символов некоторого алфавита.

К содержанию текста такая мера информации отношения не имеет. Поэтому такой подход можно назвать объективным, то есть не зависящим от воспринимающего его субъекта.

Алфавитный подход удобен при подсчете количества информации, хранимого, передаваемого и обрабатываемого техническими устройствами. Устройствам нет дела до содержательной стороны сообщений. Компьютеры, принтеры, модемы работают не с самой информацией, а с ее представлением в виде сообщений. Оценить информационные результаты их работы как полезные или бесполезные может только человек.

Алфавит – это набор букв, знаков, цифр, скобок и т.д.
Количество символов в алфавите называется его мощностью.

Например, мощность алфавита из русских букв и дополнительных символов:

33 буквы + 10 цифр + 11 знаков препинания + скобки + пробел = 54

При алфавитном подходе считается, что каждый символ текста имеет определенный информационный вес. Информационный вес символа зависит от мощности алфавита.

Какова минимальная мощность алфавита, с помощью которого можно записывать (кодировать) информацию?

Односимвольный алфавит

Сообщение любой длины, использующее односимвольный алфавит, содержит нулевую информацию.

Доказательство:

Предположим, что используемый алфавит состоит из одного символа, например, буквы «А». Интуитивно понятно, что сообщить что-либо с помощью единственного символа невозможно.

Двоичный алфавит

Двоичный алфавит состоит из 2-х символов: 0 и 1.

Информационный вес символа двоичного алфавита называется 1 бит.

Следовательно, 1 бит – это 0 или 1.

Назовем комбинацию из 2-х, 3-х и т.д. бит двоичным кодом.

Сколько символов можно закодировать двумя битами?

Порядковый номер символа
Двухзначный двоичный код

Отсюда следует, что в алфавите мощностью 4 символа информационный вес каждого символа - 2 бита.

Сколько символов можно закодировать тремя битами?

Порядковый номер символа
Трехзначный двоичный код

Отсюда следует, что в алфавите мощностью 8 символов информационный вес каждого символа - 3 бита.

Можно сделать вывод, что в алфавите мощностью 16 символов информационный вес каждого символа будет 4 бита.

Обозначим мощность алфавита буквой N, а информационный вес символа буквой b.

Зависимость между мощностью алфавита N и информационным весом символа b.

N
b	1 бит	2 бита	3 бита	4 бита

Заметим, что 2 = 2¹, 4 = 2², 8 = 2³, 16 = 2⁴.

Таким образом, можно сделать вывод:

Информационный вес каждого символа, выраженный в битах (b), и мощность алфавита (N) связаны между собой формулой:
N = 2^b

Практические задания

Задание 1

“Вы выходите на следующей остановке?” – спросили человека в автобусе. “Нет”, – ответил он. Сколько информации содержит ответ?

Решение: человек мог ответить только “Да” или “Нет”, т.е. выбрать один ответ из двух возможных. Поэтому N = 2. Значит I = 1 бит (2 = ).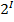

Ответ: 1 бит.

Задание 2

“Петя! Ты пойдешь, сегодня в кино?” – спросил я друга. “Да”, – ответил Петя. Сколько информации я получил?

Решение: Петя мог ответить только “Да” или “Нет”, т.е. выбрать один ответ из двух возможных. Поэтому N = 2. значит I = 1 бит (2 = 2¹).

Ответ: 1 бит.

Задание 3

Сколько информации содержит сообщение, уменьшающее неопределенность знаний в 8 раз?

Решение: так как неопределенность знаний уменьшается в 8 раз, следовательно, она было равна 8, т.е. существовало 8 равновероятных событий. Сообщение о том, что произошло одно из них, несет 3 бита информации (8 = 2³).

Ответ: 3 бита.

Задание 4

Какой объем информации содержит сообщение, уменьшающее неопределенность в 4 раза?

Решение: так как неопределенность знаний уменьшается в 4 раз, следовательно, она было равна 4, т.е. существовало 4 равновероятных событий. Сообщение о том, что произошло одно из них, несет 2 бита информации (4 = 2²).

Ответ: 2 бита.

Задание 5

Вы подошли к светофору, когда горел желтый свет. После этого загорелся зеленый. Какое количество информации вы при этом получили?

Решение: из двух сигналов (желтого и зеленого) необходимо выбрать один – зеленый. Поэтому N = 2, а I = 1 бит.

Ответ: 1 бит.

Задание 6

Группа школьников пришла в бассейн, в котором 4 дорожки для плавания. Тренер сообщил, что группа будет плавать на дорожке номер 3. Сколько информации получили школьники из этого сообщения?

Решение: из 4 дорожек необходимо выбрать одну, т.е. N = 4. Значит по формуле I = 2, т.к. 4 = 2².

Пояснение: номер дорожки (3) не влияет на количество информации, так как вероятности событий в этих задачах мы приняли считать одинаковыми.

Ответ: 2бита.

Задание 7

На железнодорожном вокзале 8 путей отправления поездов. Вам сообщили, что ваш поезд прибывает на четвертый путь. Сколько информации вы получили?

Решение: из 8 путей нужно выбрать один. Поэтому N = 8, а I = 3, т.к. 8 =2³.

Пояснение: номер пути (4) не влияет на количество информации, так как вероятности событий в этих задачах мы приняли считать одинаковыми.

Ответ: 3 бита.

Задание 8

В коробке лежат 16 кубиков. Все кубики разного цвета. Сколько информации несет сообщение о том, что из коробки достали красный кубик?

Решение: из 16 равновероятных событий нужно выбрать одно. Поэтому N = 16, следовательно, I = 4 (16 = 2⁴).

Пояснение: события равновероятны, т.к. всех цветов в коробке присутствует по одному.

Ответ: 4бита.

Задание 9

Была получена телеграмма: “Встречайте, вагон 7”. Известно, что в составе поезда 16 вагонов. Какое количество информации было получено?

Решение: так как из 16 вагонов нужно выбрать один, то N = 16, следовательно, 1 = 4(16 = 2⁴).

Ответ: 4 бита.

Задание 10

При угадывании целого числа в диапазоне от 1 до N было получено 9 бит информации. Чему равно N?

Решение: N = 2⁹= 512.

Ответ: диапазон чисел имеет значение от 1 до 512.

Задание 11

При угадывании целого числа в некотором диапазоне было получено 8 бит информации. Сколько чисел содержит этот диапазон?

Решение: N = 2⁸= 256.

Ответ: 256 чисел.

Задание 12

Сообщение о том, что ваш друг живет на 10 этаже, несет 4 бита информации. Сколько этажей в доме?

Решение: N = 2⁴= 16 этажей.

Пояснение: события равновероятны, т.к. номера этажей не повторяются.

Ответ: 16 этажей.

Задание 13

Сообщение о том, что Петя живет во втором подъезде, несет 3 бита информации. Сколько подъездов в доме?

Решение: N = 2³= 8 подъездов.

Пояснение: события равновероятны, т.к. номера подъездов не повторяются.

Ответ: 8 подъездов.

Контрольные вопросы

1. Какая наименьшая единица измерения информации вам известна.

2. Назовите более крупные производные единицы информации.

3. Опишите способ измерения информации при содержательном подходе.

4. Опишите способ измерения информации при алфавитном подходе.

Содержание отчета

1. Тема, цель.

2. Решение практических заданий.

3. Вывод.

Лабораторная работа №2

Тема:Запись чисел в различных системах счисления. Арифметические операции в различных системах счисления.

Цели:Приобрести навыки записи чисел в различных системах счисления. Изучить арифметические операции в различных системах счисления.

Ход работы

1. Изучить теоретическую часть.

2. Выполнить практические задания.

3. Ответить на контрольные вопросы.

4. Оформить отчет.

Теоретическая часть

Человеку издревле приходилось считать различные предметы, нужно было, и записывать их количество. Самой первой, вероятно, возникла унарная система записи, при которой числа обозначались соответствующим количеством черточек (или засечек на деревяшке).

Унарная запись получается очень громоздкой и неудобной, поэтому люди стали искать более компактные способы обозначать большие числа. Появились разные условные обозначения для различных чисел. Например, многие народы использовали в качестве цифр буквы, к которым добавляли специальные значки. На Руси таким знаком было

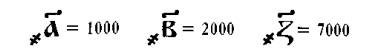
Но все равно, число получалось сложением цифр, поэтому система оставалась сложной.

Системой счисления называют совокупность символов (цифр) и правил их использования для представления чисел.

В римской системе счисления появилась одно новая идея: хотя там тоже для обозначения чисел использовали буквы, но роль их зависела от порядка записи (значение могло не только прибавляться, но и вычитаться). Развитие этой идеи привело к появлению современных позиционных систем счисления.

Мы настолько привыкли к нашей обычной – десятеричной системе, что даже не задумываемся насколько, гениальной была идея, положенная в ее основу: в позиционных системах счисления значение цифры зависит от ее позиции (места) в числе. Например, число 444 записано тремя одинаковыми цифрами, но каждая из них имеет свое значение: четыре сотни, четыре десятка и четыре единицы. То есть его можно записать вот так: 444= 4*100 + 4*10 + 4*1.

Система счисления (СС) – это способ записи чисел при помощи определенного набора цифр и букв, называемого алфавитом символов.

Системы счисления бывают позиционные (значение цифры зависит от ее положения в числе непозиционные (значение цифры независимо от ее положения в числе)

Непозиционные СС – используются для обозначения глав дат.

В этих СС значение цифры не зависит от ее положения в числе, так как каждая цифра уже имеет свой вес.

Непозиционные характеризуются готовым набором символов, каждый из которых определяет какое-то конкретное число (т.е. имеет свой вес). Остальные числа образуются от комбинации этих символов

Одна из таких СС-римская система счисления – самая распространенная. В римской СС цифровые символы обозначены знаками и буквами:

I= 1 L =50

V= 5 С =100

X= 10 М =1000

С помощью комбинаций этих символов записывается любое число.

Пример: 1969₁₀ = 1000+900+60+9 =1000 = М

900 = (1000-100) = МС

60 = (50+10) = LX

9 = (10- 1) = IX

Получаем:1969₁₀ = MMCLXIX_{римская}

Правила образования чисел в римской СС:

- чтобы выразить число, меньшее по величине, чем ближайшее к имеющемуся знаковому обозначению, нужно перед этим знаковым символом записать знаковые символы тех чисел, которые нужно вычесть из большего числа;

- чтобы выразить число, большее по величине, чем ближайшее к имеющемуся знаковому символу, то знаковые символы того числа, которое надо сложить с большим числом, надо записать справа (сзади) за этим знаковым символом.

Примеры:

4 = 5-1 будет записано так: IV.

6 = 5 + 1 будет записано: VI.

9=10-1®IX11 = 10+1®XI

40= 50- 10 ®XL60 = 50+20®LXX

Задание: перевести числа 1647, 179, 2269 в римскую СС.

В позиционных СС величина (вес) каждой цифры (знака) зависит от той позиции, которую цифра (знак) занимает в заданном числе.

Позиция цифры в числе называется разрядом. Разряд числа возрастает автоматически справа налево от младших разрядов к старшим.

Число, обозначающее систему счисления, записывается как нижний индекс справа за числом, которое мы переводим.

Позиционные СС характеризуются определенным алфавитом и основанием(базисом)системы. Базисное число – это число, определяющее количество рабочих цифр в данной СС.

Алфавит позиционной СС это набор определенных знаков (цифр и букв), используемых для изображения чисел в данной системе счисления (т.е. “рабочие цифры”).

Основание позиционной СС – это количество “рабочих цифр” в данной системе счисления.

Пример. Число 24425 состоит (справа налево):5 – единицы, 2 – десятки, 4 – сотни,4 – тысячи. 2 – десятки тысяч.

Пример. В 10-тичной СС число 555– содержит одну цифру 5, но “вес" каждой – разный:

число единиц равно 5 – (разряд единиц),

число десятков равно 5 – (разряд десятков),

число сотен тоже равно 5 – (разряд сотен).

Запись “555” – это свернутая форма записи числа в десятичной СС (привычная нам). Развернутая форма (полная) записи этого числа 555 такая:555 =5*100+5*10+5 1=5*10²+5*10¹+5*10⁰.

Получаем:555₁₀= 5*10² +5* 10¹ + 5*10⁰.

Из такой записи видим, что в позиционной СС число записывается в виде суммы числового ряда степеней основания (у нас это число = 10), в качестве коэффициентов которых выступают цифры (знаки) данного числа.

Для записи целых чисел показатель основания записывают как число положительное. Для записи десятичных дробей указывают значения степеней основания так: в целой части – положительные значения, увеличивая их от нуля справа налево в дробной части – отрицательные значения, увеличивая их с единицы слава направо.

Пример:555.55₁₀=5*10²+5*10¹+5*10⁰+5*10^-1+5*10^-2= 5*100+5*10+5*1+5*0.1+5*0.01=500+50+5+0.5+0,05=550+0.55=555.55₁₀;

Правило. Любое число в любой позиционной СС можно представить в виде формулы:

A_g=a_m-1*g^m-1+ a_m-2*g^m-2+ a_m-3*g^m-3+…+a₀*g⁰+a_-1*g^-1+a_-2*g^-2+…+a_-n*g^-n,

где А – заданное число,

g – основание СС заданного числа (),

а – значения цифр в каждом разряде заданного числа (в формуле это коэффициенты).

m – количество цифр в целой части числа,

n – количество цифр в дробной части числа (запись дробной части выделена синим цветом).

В настоящее время наиболее распространены десятичная, двоичная, восьмеричная и шестнадцатеричная системы счисления.

Таблица 1. Соотношения простых чисел:

п=10	п=2	n=8	п=16
j
			А
			B
			С
			D
			Е
			F

Задание 1.

Записать в тетради общие формулы представления чисел в развернутой форме в 2-ичной. 8-ричной, 16-ричной, 10-тичной системах счисления.

В программах для ЭВМ используются следующие системы счисления

Наименование системы счисления	Основание системы n	Рабочие цифры и символы(a)	Количество рабочих цифр (m)
Десятичная		0,1.2,3,4,5,6,7,8,9
Двоичная		0,1
Восьмеричная		0,1.2,3,4,5,6,7
Шестнадцатеричная		0,1.2,3,4,5,6,7,8,9,A,B,C,D,E,F

Примеры записи чисел в разных системах счисления:

Десятичная СС: 689₁₀=6*10²+8*10¹+9*10⁰

Двоичная СС: 100101₂=1*2⁵+0*2⁴+0*2³+1*2²+0*2¹+1*2⁰

Восьмеричная: 642₈=6*8²+4*8¹+2*8⁰

Шестнадцатеричная СС: 2A4F₁₆=2*16³+A*16²+4*16¹+F*16⁰,где A=10,F=15