Исследование взаимосвязей количественных показателей.

Для оценки тесноты связей количественных признаков (измеряемых числами) используются различные показатели. Основными из них являются следующие.

1. Линейный коэффициент корреляции r_xy выражает степень тесноты

линейной связи между двумя случайными величинами X иY (нормированный корреляционный момент).

По выборочным данным линейный коэффициент корреляции вычисляется по формуле:

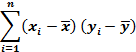
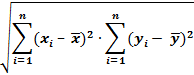
где n – объем выборки;

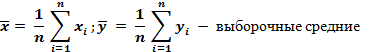
Свойства коэффициента корреляции:

1) r_xy = r_xy = r (X,Y) = r (aX + b,cY + d).

2) -1 ≤ r_xy ≤1.

3) Если r_xy = ±1, то Y и X точно связаны линейной функциональной зависимостью.

4) Если r_xy = 0, то между Y и X нет линейной корреляционной зависимости, но равенство r_xy =0 не исключает существования какого-либо другого вида корреляционной зависимости – криволинейной (например, параболической, показательной и др.)

5) Чем больше 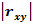, тем теснее связь между X и Y.

При этом связь сильная, если 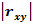= 0,7÷1; связь умеренная, если

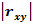=0,5 ÷ 0,7; связь слабая, если 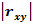= 0,3 ÷ 0,5; связь практически отсутствует при 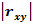< 0,3.

6) Если r_xy > 0, то имеет прямую корреляционную связь; если r_xy < 0, то имеет обратную корреляцию (если с увеличением значения X возрастает и значение Y, то между X и Y существует прямая связь; изменение значений признаков в противоположных направлениях свидетельствует об обратной связи между ними).

Коэффициент корреляции не изменяется при линейных преобразованиях переменных. Если имеет уравнения регрессии в виде,

,

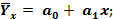
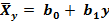то коэффициент корреляции выражается через коэффициент регрессии по соотношению:

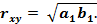
Здесь 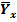– среднее значений величины Y при значении X = x;

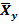– среднее значений величины X при значении Y = y.

Проверка гипотезы о значимости выборочного парного линейного коэффициента корреляции 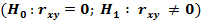осуществляется с использованием T-критерия Стъюдента

=

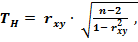
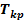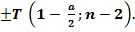
1. Эмпирическое корреляционное отношение 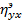применяется для оценки тесноты нелинейной связи между случайными величинами X и Y, представленными виде сгруппированных статистических данных.

Обычно исходные данные могут быть собраны в следующую таблицу значений системы двух случайных величин (X, Y):

Таблица 1

Таблица значений системы двух случайных величин

X Y	y1	Y2	…	yj	…	ym
x1	n11	n12	…	n1i	…	n1m
x2	n21	n22	…	n2i	…	n2m
…	…	…	…	…	…	…
xi	ni1	ni2	…	nij	…	nij
…	…	…	…	…	…	…
xk	nk1	nk2	…	nkj	…	nkm

Здесь n_ij – частоты, показывающие сколько раз повторяются парные значения

( X = x_i, Y = y_i).

При этом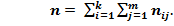

По данной таблице можно вычислить следующие параметры:
1) среднее значения величин X и Y:

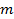
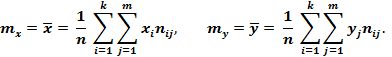
2) дисперсии величин X и Y:

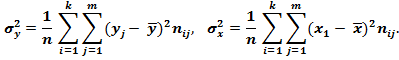
3) средние значения Y при фиксированном x_i , то есть средние по строкам (межгрупповые средние):

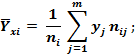
4) средние значения X при фиксированном y_i :

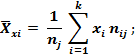
5) межгрупповую дисперсию:

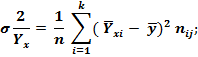
6) остаточную дисперсию:

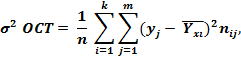
7) общую дисперсию:

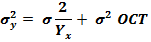
Здесь

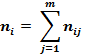
- такое число раз встречалось значение x_i;

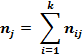
- такое число раз встречается значение y_i.

Тогда статистическое корреляционное отношение вычисляется по формуле:

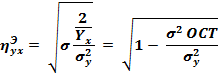
Оно показывает, какую часть общей изменчивости составляет межгрупповая изменчивость.

Свойства эмпирического корреляционного отношения:

1)

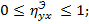
2) Если 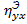= 1, то между существует функциональная связь; если 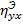= 0, то Y и X являются независимыми величинами;

3)

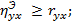
4) 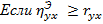, то связь между Y и X является линейной.

Степень расхождения между 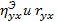может служить основанием для принятия гипотезы о линейности связи между переменными Y и X.

При этом используется критерий

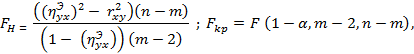
Где n – число наблюдений; m - число сгруппированных интервалов для показателя Y.

На практике часто при проверке возможности использования линейной функции в качестве формы уравнения регрессии определяют разность 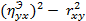. Если эта разность менее 0.1, то считается возможным применять линейные уравнения для описания корреляционной зависимости.

Следует отметить, что вычисление корреляционного отношения возможно при наличии достаточно большого числа данных, которые представлены либо в форме корреляционной таблицы, либо первичными данными. Вычисление корреляционного отношения при большом числе групп и малом числе наблюдений в каждой группе лишается смысла.

Проверка значимости эмпирического корреляционного отношения 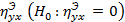осуществляется по критерию

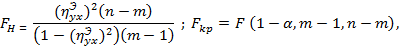
Где n– число опытов, m - число интервалов (групп) различных значений Y.

Пример. По 50 наблюдениям оценили тесноту связи двух экономических показателей с помощью статистического корреляционного отношения и линейного коэффициента корреляции.

Получили следующие оценки параметров (при группировке показателя Y на 5 интервалов): 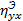= 0.77; 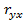= 0.68. Какую форму регрессивной зависимости следует искать: линейную или нелинейную?

Решение.Проверим гипотезу о линейности связи между переменными (проверяемая гипотеза: различие между статистическим корреляционным отношением и линейным коэффициентом корреляции незначимо).

Тогда по критерию Фишера получаем

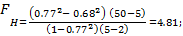
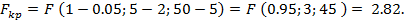
Вывод: целесообразно использовать нелинейную регрессию.

3. Теоретическое корреляционное отношение (индекс корреляции) 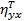(или просто 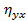). Формы расчета 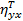аналогичны формулам для 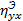за исключением того, что используется не групповые средние 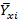, а значения функции регрессии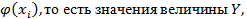

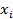связь Y и X при значении . Фактически, 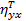оценивает степень близости кривой регрессии к имеющимся данным, то есть степень удачности выбора уравнений регрессии.

Для 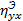и 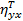имеет место неравенства 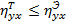. Оно справедливо потому, что кривая регрессии не всегда проходит через групповые средние.

Проверка значимости индекса корреляции (теоретического корреляционного отношения 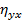) 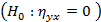осуществляется по критерию

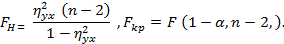
4. Коэффициент множественной корреляции характеризует тесноту связи между одним и несколькими независимыми показателями.

Если имеются m показателей (X₁,X₂, … X _j-1, X_j+1, … X_m), то выборочный коэффициент множественной корреляции показателя (X _j) характеризует тесноту линейной связи между этим зависимым и остальными независимыми показателями (X₁,X₂, … X _j-1, X_j+1, … X_m) и вычисляется по формуле

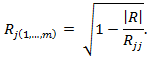
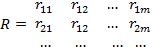
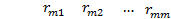
R_jj - алгебраическое дополнение элемента r_jj матрицы R.

В случае зависимости результирующей величины от двух переменных Y = 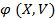коэффициент множественно корреляции вычисляется по формуле:

.

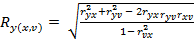5.Частные (парциальные) коэффициенты корреляциииспользуются для оценки тесноты связи между двумя показателями из нескольких при элиминированном (исключенном) влиянии других показателей.

Если имеются m показателей (X₁,X₂, … X_m), то частный коэффициент корреляции показателей (X_j,X_k) вычисляется по формуле

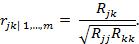
Пусть мы имеем три показателя X,Y,V. Частный коэффициент корреляции между Y и X при исключении V определяется через парные коэффициенты корреляции соотношением:

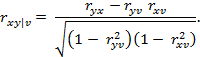
абсолютные величины частых (парциальных) коэффициентов корреляции не могут быть больше величины коэффициента множественной корреляции.

6. Коэффициент детерминации R² есть квадрат коэффициента корреляции (для линейной связи), или квадрат корреляционного отношения (для нелинейной зависимости) величин X и Y, или квадрат коэффициента множественной корреляции 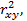R² = 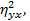R² = R² =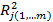

Пример. Исследовалась взаимосвязь между тремя показателями: производительностью труда (X₁), возрастом(X₂), и производственным стажем (X₃). По выбору из 100 рабочих одной и той же специальности вычислены парные коэффициенты корреляции: r₁₂ = 0.2, r₁₃ = 0.41, r₂₃ = 0.82. Вычислить множественные и частные (парциальные) коэффициенты корреляции. Оценить значимость этих коэффициентов.

Решение. Вычислим множественные коэффициенты корреляции, характеризующие связь между одним зависимым и двумя независимыми показателями.

.

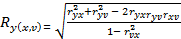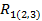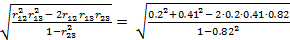= = 0.47;

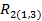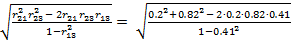= = 0.83;

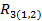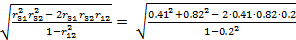= = 0.86;

Оценим значимость вычисленных множественных коэффициентов корреляции при уровне значимости α = 0.05.

Проверка гипотезы о значимости множественного коэффициента корреляции 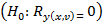осуществляется с использованием F – критерия. Вычислим наблюдаемое значение критерия:

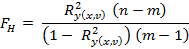
Где n = 100 – объем выборки, m = 3 – количество показателей.

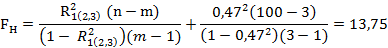
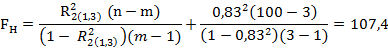
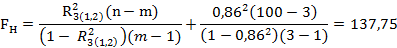
По таблице квантилей F – распределения найдем критическую точку.

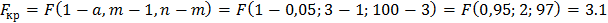
Так как 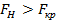, то гипотезу 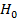отвергаем, то есть множественные коэффициенты корреляции значимы.

Вычислим частные (парциальные) коэффициенты корреляции, характеризующие связь между двумя показателями при исключенном влиянии третьего.

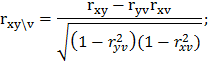
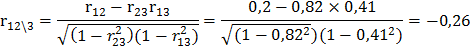
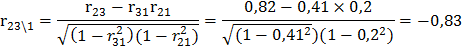
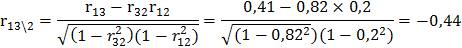
Оценим значимость вычисленных частных (парциальных) коэффициентов корреляции при уровне значимости a=0,05

Проверка гипотезы о значимости частного коэффициента корреляции

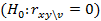осуществляется с использованием T- распределения Стьюдента.

Вычислим наблюдаемое значение критерия:

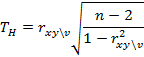
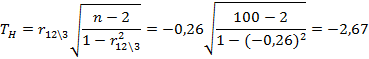
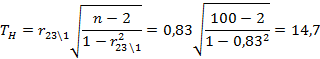
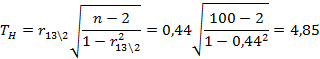
По таблице квантилей T - распределения Стьюдента найдем критическую точку.

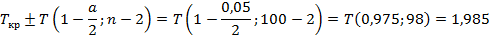
Так как 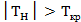, то гипотезу 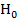отвергаем, то есть частные 9парциальные) коэффициенты корреляции значимы.