Условные законы распределения

Для того, чтобы охарактеризовать зависимость между составляющими двумерной случайной величины, вводится понятие условного распределения.

Условным законом распределениясоставляющей x, входящей в систему (X,Y),называется ее закон распределения, вычисленный при условии, что другая случайная величина Yприняла определенное значение y. Аналогично определяется условный закон составляющей Y.

Рассмотрим дискретную двумерную случайную величину (X,Y). Пусть возможные значения составляющих таковы: x₁,x₂,…,x_m и y₁,y₂,…,y_n. Обозначим условную вероятность того, что X примет значение x_i при условии, что Y = y_j, через P(x_i│y_j).Условная вероятность P(x_i│y_j), вообще говоря, не будет равна безусловной вероятности P(x_i).

Условным распределением составляющей X при Y = y_j называют совокупность условных вероятностей:

P(x₁│y_j), P(x₂│y_j), …, P(x_m│y_j).

Аналогично определяется условно распределение Y при X = x_i:

P(y₁│x_i), P(y₂│x_i), …, P(y_n│x_i).

Зная закон распределения двумерной дискретной величины, можно вычислить условные вероятности составляющих:

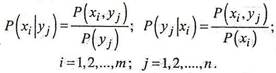
Сумма вероятностей условного распределения равна единице.

Рассмотрим теперь двумерную непрерывную случайную величину (X,Y).

Условной плотностью распределения составляющей X при заданном значении Y=y называют отношение плотности совместного распределения системы к плотности распределения составляющей Y:

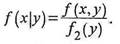
Отличие условной плотности f (x│y) от безусловной плотности f₁(x) состоит в том, что функция f (x│y) дает распределение X при условии, что составляющая Y приняла значение y, а функция f₁(x) дает распределение X независимо от того, какие из возможных значений приняла составляющая Y.

Аналогично определяется условная плотность распределения составляющей Y:

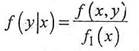
Свойства условных плотностей распределения:

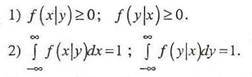
Если условные плотности распределения случайных величин Xи Y равны их безусловным плотностям, то величины Xи Yявляются независимыми.

Случайные величины Xи Yназываются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае величины X и Yназываются зависимыми.

Для того чтобы случайные величины Xи Yбыли независимыми, необходимо и достаточно, чтобы

F(x,y) = F_l(x)F₂(y)

или

f(х,у)= f₁ (х) f2(у).

Зная закон распределения системы двух случайных величин, можно всегда определить законы распределения отдельных величин, входящих в систему (маргинальныезаконы распределения).

Рассмотрим непрерывную двумерную случайную величину.

Так как 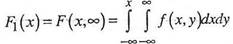, то, дифференцируя последнее выражение по х, будем иметь:

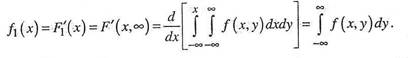
Аналогично,

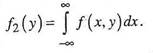
Зная f(х,у), легко определяются f(х) и f(у).

Чтобы определить f(х,у) по f(х) и f(у), надо знать условные законы распределения.