Трубопроводы с кольцевыми участками.

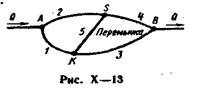
Кольцевой разветвленный участок представляет собой в простейшем случае две параллельные трубы между узлами АиВс одной или несколькими перемычками, соединяющими промежуточные сечения этих труб (рис. X—13). По перемычкам некоторое количество жидко­сти перетекает из одной трубы в другую. Направление по­тока в перемычке опреде­ляется величинами напоров в соединяемых перемычкой сечениях. Жидкость может подаваться в кольцевой раз­ветвленный участок или отби­раться из него через узлы А и В смыкания участка с под­водящей и отводящей трубами или через узлы К и S на концах перемычек.

При аналитическом расчете трубо­провода с кольцевыми участками применяют метод по­следовательных приближений. Например, если при за­данных размерах труб кольцевого участка известны величины притока и отбора жидкости в узлах и требуется определить расходы в трубах, то в качестве первого при­ближения эти расходы 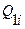задают удовлетворяющими условиям баланса расходов в узлах. Затем выбирают первое замкнутое кольцо разветвленного участка, и для всех входящих в него труб вычисляют потери напора. Расходы считаются заданными правильно, если алгебраи­ческая сумма потерь напора в кольце равна нулю. В про­тивном случае следует повторить выкладки при изме­ненных расходах в трубах:

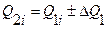
Поправка 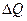должна удовлетворять уравнению

Подбор расходов следует продолжать до тех пор, пока алгебраическая сумма потерь напора в трубах рассма­триваемого кольца не станет равной нулю. Затем анало­гичные вычисления повторяют последовательно для каж­дого из замкнутых контуров разветвленного участка.

Расчет кольцевых трубопроводов с заданными раз­мерами в простых случаях можно проводить графическим способом. Рассмотрим такой способ применительно к схеме кольцевого участка на рис. X—13, предполагая, что жидкость подается в кольцо через узел А и отбирается из кольца через узел В.

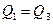
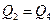При графическом решении задачи первоначально пред­полагаем, что перемычка KS перекрыта. В этом пред­положении и ; кроме того,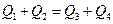

Для определения направления потока в перемычке составляют уравнения характеристик труб 1—4:

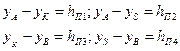(5.37)

где 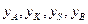— напоры в узлах; — потери на­пора в трубах, подсчитываемые по уравнению (1).

Вопросы для самопроверки.

1. Какие трубопроводы называются короткими и длинными, прос­тыми и сложными?

2. Какие типы уравнений используют при расчете трубопроводов?

3. Какие типы задач могут быть при расчете трубопроводов?

4. Как рассчитывают трубопроводы при параллельном и последо­вательном соединении?

5. Что такое сифонный трубопровод и как его рассчитать?

Раздел 6. ОБЩИЕ ВОПРОСЫ ГИДРОМЕХАНИКИ.

Тема 6.1. Основы теории гидродинамического подобия.

Подобие гидравлических явлений. Геометрическое, кинематичес­кое и динамическое подобие. Критерии подобия. Особенности моделиро­вания гидравлических явлений. Понятия об определяющих критериях подобия. Примеры моделирования гидравлических явлений при создании конструкций судовых машин.

Указания к теме 6.1.

1. Подобными называют такие потоки жидкости, у которых каждая характеризующая их физическая величина находится для любых сходственных точек в одинаковом отношении. Понятие гидродинамического подобия вклю­чает (рис. V—1) подобие поверхностей, ограничивающих потоки (геометрическое подобие); пропорциональность скоростей в сходственных точках и подобие траектории движения сходственных частиц жидкости (кинематическое подобие); пропорциональность сил, действующих на сход­ственные частицы жидкости и пропорциональность масс этих частиц (динамическое подобие).

Отношения однородных физических величин, постоян­ные во всех сходственных точках подобных потоков, на­зывают коэффициентами (масштабами) подобия. Соответ­ственно принятым в Международной системе единиц основ­ным физическим величинам (длина L, время Т и масса М) выделяют три основных коэффициента подобия; линейный масштаб 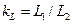,масштаб времени 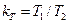и мас­штаб масс 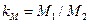. Масштабы всех остальных (произ­водных) физических величин выражаются через основные в соответствии с формулами размерности этих величин. Так, масштаб скоростей 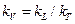,сил одинаковой фи­зической природы 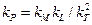,плотностей 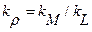и т. д.

Используя выражения масштабов 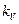и , 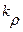можно полу­чить для масштаба сил зависимость

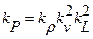, (6.1)

которая дает общий, закон динамического подобия Нью­тона:

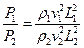(6.2)

Последний можно представить в форме

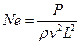, (6.3)

согласно которой безразмерная величина Ne (число Нью­тона), пропорциональная отношению действующих на по­добные частицы сил к силам инер­ции этих частиц, имеет одинаковое значение в сходственных точках по­добных потоков.

2. Для рассматриваемого ниже установившегося движения однород­ных несжимаемых жидкостей необ­ходимыми и достаточными условиями гидродинамического подобия явля­ются:

а) геометрическое подобие гра­ничных поверхностей, омываемых потоками (включая в некоторых случаях и подобие шероховатостей стенок);

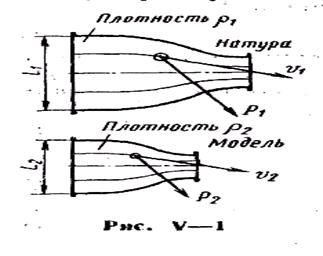
б) подобие кинематических краевых условий (подобное распределение скоростей во входных и выходных сече­ниях рассматриваемых объектов — каналов, местных со­противлений и т. д.);

в) одинаковые значения критериев динамического по­добия — безразмерных величин, пропорциональных отно­шениям сил инерции частиц жидкости к действующим на них силам вязкостного трения (число Рейнольдса Re) и
силам тяжести (число Фруда Fr).

Условием пропорциональности сил инерции и сил вяз­костного трения является одинаковое значение числа Re для потоков в натуре и модели

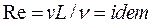, (6.4)

где v— характерная (обычно средняя в сечении) скорость; L — характерный размер (обычно диаметр сечения D); 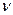— кинематическая вязкость.

Условие (4) приводит к соотношению для коэффи­циентов подобия:

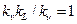(6.5)

и для скоростей в натуре и модели

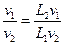(6.6)

Условием пропорциональности сил инерции и сил тя­жести является одинаковое значение числа Fr:

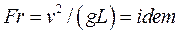(6.7)

Так как ускорение свободного падения g в натуре и модели практически всегда одинаково (масштаб ускоре­ний; к_g = 1), условие (7) приводит к соотношению для коэффициентов подобия

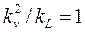(6.8)

и для скоростей в натуре и модели

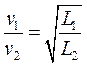(6.9)

Подобие потоков в натуре и модели требует одновре­менного выполнения условий (4) и (7) для чисел Rе и Fr или условий (5) и (8) для коэффициентов по­добия. Последнее возможно только тогда, когда масштабы линейных размеров и вязкостей находятся в соотношении

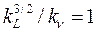(6.10)

из которого следует, что в модели меньших по сравнению с натурой размеров должна применяться менее вязкая жидкость:

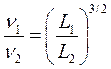(6.11)

При выполнении условий подобия все безразмерные характеристики потока, т. е. безразмерные комбинации различных физических величин (например, коэффициенты сопротивления 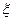, скорости 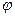, расхода 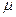и т. д.), имеют в натуре и модели одинаковое численное значение.

Моделируя поток некоторой жидкости при заданном геометрическом масштабе объектов 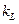(рис. V—2), необ­ходимо применить в модели другую жидкость, вязкость которой будет удовлетворять условию (11). Выполнение при этом условия (9) для скоростей требует опре­деленного соотношения между располагаемыми перепа­дами пьезометрических уровней (гидростатическими на­порами) Н для натурного объекта и его модели. Так как по уравнению Бернулли любая характерная скорость мо­жет быть выражена как 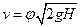(где 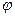— безразмер­ный коэффициент скорости), получаем

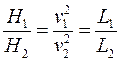(6.12)

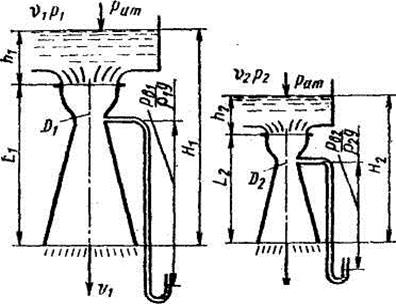т. е. располагаемые гидростатические напоры должны быть пропорциональны линейным размерам объектов.

Рис. V—2

При выполнении условий подобия масштаб времени 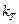для процессов течения в натуре и модели определяется принятым линейным масштабом 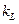и масштабом скоростей, равным по формуле (8)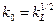

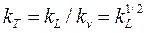
Указанные соотношения позволяют выразить масштабы всех производных физических величин как функции двух независимых масштабов — 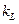и к 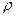. Так, для масштаба сил, исходя из формулы (1), имеем

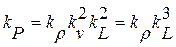
Для масштаба расходов 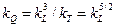потерь напора 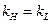,перепадов давлений

.

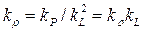3. В большинстве случаев реализация условия (11) технически весьма затруднительна или невозможна. По­этому в практике моделирования обычно осуществляют частичное подобие потоков, при котором выполняется условие подобия главных сил, наиболее существенных для рассматриваемого гидравлического явления.

Если характер движения в основном определяется свойствами инертности и весомости жидкости, а влияние вязкости относительно невелико (безнапорные русловые потоки, истечение маловязких жидкостей через большие отверстия и водосливы, волновые движения и т. д.), мо­делирование осуществляется по критерию гравитацион­ного подобия. При этом выполняется условие (9) для скоростей, а условие равенства чисел Рейнольдса, приво­дящее к соотношению (11), не соблюдается (натура и модель работают обычно на одной и той же жидкости). При моделировании по числу Fr масштабы всех физиче­ских величин (за исключением вообще произвольного 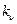)выражаются через два независимых масштаба 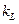и 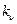таким же образом, как и при выполнении условий пол­ного подобия (табл. 1).

4. При напорном движении жидкости (для которого характерно отсутствие свободной поверхности) силы тя­жести не влияют на распределение скоростей в потоке, и для обеспечения кинематического подобия потоков вы­полнения условия гравитационного подобия не требуется. Вместе с тем характер движения существенно зависит от соотношения сил инерции и вязкости жидкости, поэтому моделирование напорных потоков осуществляется по кри­терию вязкостного подобия. Скорости в натуре и модели должны при этом удовлетворять соотношению (6) и определяться выбранными по условиям эксперимента
масштабам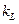и и 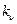. Если жидкости одинаковы ( 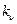= 1), то

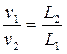(6.13)

Вопросы для самопроверки.

1.Какие потоки являются геометрически, кинематически и динами­чески подобными?

2. Сформулируйте условия гидродинамического подобия потоков и гидравлических машин.

3. Поясните физический смысл критерия Ньютона, Рейнольдса, Фруда и Эйлера.

4. Какая сила, действующая на поток жидкости, считается глав­ной действующей силой при моделировании по числу Фруда? По числу Рейнольдса?