Тема 5.2. Расчет простых и сложных трубопроводов.

Трубопроводы постоянного и переменного сечения. Сифонный трубопровод. Последовательное и параллельное соединение трубопроводов. Трубопровод с насосной подачей. Расчет судового трубопровода.

Указания к теме 5.1.

Любая система на судне, будьто система энергетической уста­новки /например, топливная, охлаждения двигателя, питательная паро­вого котла/ или общесудовая /например, пожарная, осушения/, сос­тоит из трубопроводов и гидравлических машин. Каждый инженер должен знать и уметь выполнять расчеты трубопроводов, так как впрактичес­кой деятельности приходится вносить изменения, реконструк­цию той или иной системы.

В зависимости от длины и условий работы различают два типа трубопроводов: короткие и длинные. Короткими называют такие трубопро­воды, в которых местные потери являются значительными и составляют не менее 5-10 % от потерь напора по длине. Длинными называют трубопроводы, имеющие значительную протяженность, в которых потери напо­ра по длине являются основными.

В зависимости от гидравлической схемы работы трубопроводы подразде­ляются на простые /не имеющие ответвлений/ и сложные.

1. Простым трубопроводом называют трубопровод, по которому жидкость транспортируется от питателя к прием­нику без промежуточных ответвлений потока (рис. IX—1). Питателями и приемниками в гидросистемах могут являться различные устройства — насосы и гидродвигателн, аккумуляторы, резервуары и др.

Трубопровод может иметь постоянный диаметр по всей длине или же состоять из ряда последовательно соеди­ненных участков различного диаметра.

Исходным при расчетах простого трубопровода яв­ляется уравнение баланса напоров (уравнение Бернулли) для потока от сечения а в питателе перед входом в трубо­провод до сечения b в приемнике после выхода жидкости из трубопровода. При установившемся движении жидко­сти:

,

где — сумма потерь напора на пути между выбран­ными сечениями, состоящая из потерь на трение по длине и потерь в местных сопротивлениях, расположенных на трубопроводе (к местным потерям напора относятся также потеря при входе потока из питателя в трубопровод и при выходе потока из трубопровода в приемник).

Для удобства расчетов вводится понятие располагае­мого напора трубопровода

,

который представляет перепад гидростатических напоров в питателе и приемнике и выражается разностью пьезо­метрических уровней в сечениях а и b.

Преобразуя уравнение баланса напоров, получаем общий вид расчетного уравнения простого трубопровода:

(5.1)

Если площади сечений питателя и приемника доста­точно велики по сравнению с сечением трубопровода (например, трубопровод, соединяющий два больших ре­зервуара), скоростными напорами жидкости в этих сече­ниях при составлении баланса напоров можно пренебречь. При этом расчетное уравнение приобретает вид

(5.2)

отвечая процессу, в котором весь располагаемый напор затрачивается на преодоление гидравлических сопротив­лений.

Уравнение (2) применимо также независимо от размеров питателя и приемника в тех случаях, когда трубопровод имеет достаточно большую длину, при кото­рой скоростные напоры на входе и выходе из трубопровода оказываются пренебрежимо малыми по сравнению с по­терями напора на трение по его длине.

1. 2. Применим уравнение (2) к простому трубопро­воду, который соединяет два больших резервуара с по­стоянными уровнями жидкости и состоит из k последова­тельных участков длиной l_l и диаметром d_l (рис. IX—2). Заметим, что показанные на схеме уровни жидкости в резервуарах следует рассматривать в более общем смысле как пьезометрические уровни в питателе и прием­нике.

Выражая потери на трение по длине и местные потери напора общими формулами

;

получим

,

где и — коэффициент сопротивления трения и сум­марный коэффициент местных сопротивлений на каждом участке; — средняя скорость потока в каждом участке;v_k — средняя скорость потока в выходном сечении трубо­провода; — потеря напора при выходе из тру­бопровода в резервуар, равная скоростному напору потока в выходном сечении трубопровода (для турбулент­ного режима коэффициент кинетической энергии ; для ламинарного режима в круглой трубе ).

Используя уравнение расхода

, (5.3)

получим расчетное уравнение трубопровода в виде

, (5.4)

где F_k — площадь выходного сечения трубопровода; F_i —площадь сечения участка диаметром d_i.

Для простого трубопровода длиной l и постоянным диаметром уравнение (4) при турбулентном режиме имеет вид:

, (5.5)

где — сумма коэффициентов местных сопротивлений в трубопроводе.

Выражая скорость через расход и определяя числовой множитель при g = 9,81 м/с², получим:

(5.6)

где l, d, Н — в м; Q— в м³/с.

В ряде задач на определение пропускной способности трубопровода при турбулентном режиме движения целе­сообразно приводить уравнение (5) к виду

,

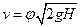где - коэффициент скорости трубопровода.

При этом расход выражается формулой:

, (5.7)

где — коэффициент расхода и — пло­щадь сечения трубопровода.

При истечении жидкости из большего резервуара через трубопровод в атмосферу (рис. IX —3) уравнение Бернулли имеет вид:

, (5.8)

где H — располагаемый напор трубопровода, опреде­ляемый высотой пьезометрического уровня в резервуаре-питателе над центром выходного сечения трубопровода; — скоростной напор в выходном сечении;

— сумма потерь напора в трубопроводе.

Так как потеря напора при выходе потока из трубо­провода в данном случае отсутствует, уравнение (8) при подстановке в него выражений потерь переходит в уравнение (4). Следовательно, приведенные выше расчетные зависимости являются общими для трубо­провода при истечении, как под уровень, так и в атмосферу.

1. 3. Графики напоров, построение которых дано на рис. IX—2 и IX—3, показывают изменение по длине трубо­провода полного напора потока и его составляющих. Линия напора (удельной механической энергии потока) строится путем последовательного вычитания потерь, нарастающих вдоль потока, из начального напора потока (заданного пьезометрическим уровнем в питающем резервуаре). Пьезометрическая линия (дающая изменение гидростатического напора потока) строится путем вычи­тания скоростного напора в каждом сечении из полного напора потока.

Пьезометрический напор 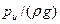в каждом сечении (р_и — избыточное давление) определяется на графике заглублением центра сечения под пьезометрической ли­нией; скоростной напор — вертикальным расстоя­нием между пьезометрической линией и линией напора. Построение графика напоров для вертикального трубо­провода дано на рис. IX—4. Напоры в каждом сечении откладываются по горизонтали таким образом, чтобы ось трубы являлась началом отсчета пьезометрических на­поров.

1. 4. Если часть длины трубопровода находится под вакуумом (например, сифонный трубопровод, рис. IX—5), необходимо проверить наибольший вакуум в опасном сечении С:

, (5.9)

где h — высота сечения С над начальным пьезометриче­ским уровнем в баке-питателе;

v—скорость в этом сечении;

- сумма потерь напора на участке трубопровода для этого сечения.

Для обеспечения нормальной (бескавитационной) ра­боты трубопровода должно выполняться условие:

,

где — атмосферное давление; —давление насы­щенных паров жидкости при данной температуре.

1. 5. При достаточно большой относительной длине l/d трубопровода скоростной напор v²/(2g) пренебрежимо мал по сравнению с общей потерей напора в трубопроводе.

Поэтому для длинного трубопровода постоянного диа­метра расчетное уравнение (5) или (6) можно заменить приближенным:

(5.10)

При расчете длинных трубопроводов, в которых доми­нируют потери на трение по длине, целесообразна замена местных сопротивлений эквивалентными длинамипо со­отношению

. (5.11)

При такой замене расчетное уравнение (10) можно представить в виде, характерном для трубопровода без местных сопротивлений:

,(5.12)

где— приведенная длина трубопровода.

Для трубопровода, состоящего из k последовательных участков различного диаметра, имеем аналогичное соот­ношение:

(5.13)

График напоров для длинного трубопровода строится упрощенно (рис. IX—6), поскольку относительная малость скоростных напоров позволяет рассматривать линию, на­пора и пьезометрическую линию как практически совпадающие.

1. 6. Расчет трубопровода на основе приведенных выше соотношений связан с выбором коэффициентов местных сопротивлений 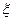и коэффициента сопро­тивления трения . Значения при различных режимах движения жидкости определяются следующими зависи­мостями.

а) Ламинарный режим ( ). Коэффициент сопротивления трения и потеря напора на трение

(5.14)

б) Турбулентный режим ( )

Область гидравлически гладких труб. Коэффициент сопротивления трения можно определить по формуле Конакова:

(5.15)

и по формуле Блазиуса :

, (5.16)

в соответствии, с которой потеря напора на трение (ве­личины — в международной системе единиц)

(5.17)

Зависимость от Re для гидравлически гладких труб

Re		Re		Re
4 000	0,0400	40 000	0,0225	400 000	0,0140
6 000	0,0360	60 000	0,0200	600 000	0,0130
8 000	0,0335	80 000	0,0190	800 000	0,0120
10 000	0,0315	100 000	0,0180	1 000 000	0,0115
15 000	0,0285	150 000	0,0165	2 000 000	0,0105
20 000	0,0270	200 000	0,0155	3 000 000	0,0100

К указанной области сопротивления относятся техни­чески гладкие трубы (цельнотянутые из цветных метал­лов — медные, латунные, свинцовые, стеклянные трубы и др.) во всем диапазоне их практического использования по числам Re, а также стальные трубы до значений числа Рейнольдса, ориентировочно равных (здесь — эквивалентная абсолютная шероховатость).

Переходная область. Значения в функции Re и относительной гладкости для стальных труб, по данным Мурина (Всесоюзный теплотехнический институт им Ф. Э. Дзержинского), приведены на графике при­ложения 2.

Близкие к опытным значениям результаты дает уни­версальная формула Альтшулля (применимая во всех областях турбулентного режима)

(5.18)

Средние значения эквивалентной шероховатости для новых стальных цельнотянутых труб = 0,1 мм и быв­ших в употреблении (незначительно корродированных) = 0,2 мм. Верхняя граница переходной области ориен­тировочно определяется выражением:

.

Область гидравлически шероховатых труб (ква­дратичная область).

Значения в функции даются формулой Никурадзе

(5.19)

или близкой к ней формулойШифринсона

(5.20)

Для старых водопроводных (стальных и чугунных) труб, значительно корродированных в результате дли­тельной эксплуатации ( мм), применимо также выражение (d в м)

(5.21)

Зависимость от Re в квадратичной области

	0,0379		0,0192	2 500	0,0159
	0,0304		0,0188	3 000	0,0153
	0,0269		0,0184	3 500	0,0148
	0,0249		0,0181	4 000	0,0144
	0,0234		0,0178	5 000	0,0137
	0,0223		0,0176	6 000	0,0132
	0,0216		0,0173	7 000	0,0128
	0,0207		0,0171	8 000	0,0125
	0,0202		0,0169	9 000	0,0122
	0,0197		0,0167	10 000	0,0120

Для труб некруглого сечения (например, прямоуголь­ных, овальных и др.) потери напора на трение по длине выражаются общей формулой:

где v — средняя по сечению скорость; — гидравличе­ский диаметр сечения (представляет отношение учетве­ренной площади F сечения трубы к его периметру: и для круглой трубы совпадает с геометрическим диаметром: ).

Значения коэффициента сопротивления трения опре­деляются по формулам, приведенным выше для круглых труб, с заменой в них диаметра d на .

2. Сложный трубопровод имеет разветвленные участки, со­стоящие из нескольких труб (ветвей), между которыми распределяется жидкость, поступающая втрубопровод из питателей.

Сечения трубопровода, в которых смыкаются несколько ветвей, называются узлами.

В зависимости от структуры разветвленных участков различают следующие основные типы сложных трубо­проводов: с параллельными ветвями, с концевойраздачей жидкости, с непрерывной раздачей жидкости, с кольцевыми участками. В практике встречаются также разно­образные сложные трубопроводы комбинированного типа.

Как и при расчете простого трубопровода (см. гл. IX), можновыделить три основные группы задач расчета слож­ных трубопроводов.

a) Определение размеров труб по заданным в них расходам и перепадам напоров в питателях и приемниках.

b) Определение перепадов напоров в питателях и приемниках по заданным расходам в трубах заданных размеров.

c) Определение расходов в трубах заданных размеров по известным перепадам напоров.

Последние две группы задач представляют поверочные расчеты существующего трубопровода, выясняющие условия его работы при различных значениях гидравлических параметров.

Встречаются также задачи смешанного типа, пред­ставляющие комбинации из задач основных групп.

Для решения сформулированных задач составляется система уравнений, которые устанавливают функциональ­ные связи между параметрами, характеризующими по­токи жидкости в трубах, т. е. между размерами труб, расходами жидкости и напорами. Эта система состоит из уравнений баланса расходов для каждого узла и уравне­ний баланса напоров (уравнений Бернулли) для каждой ветви трубопровода.

Поскольку обычно сложные трубопроводы являются длинными, в уравнениях Бернулли можно пренебрегать скоростными напорами, принимая полный напор потока в каждом расчетном сечении трубопровода практически равным гидростатическому и выражая его высотой пьезо­метрического уровня над принятой плоскостью сравнения. Кроме того, в сложных трубопроводах можно также пре­небрегать относительно малыми местными потерями напора в узлах. Это значительно упрощает расчеты, по­скольку позволяет считать одинаковыми напоры потоков в концевых сечениях труб, примыкающих к данному узлу, и оперировать в уравнениях Бернулли понятием напора в данном узле.

Потери напора в трубах выражаются формулой:

,

которую для расчета удобно привести к виду (Числовой множитель в формуле (1)равен , где уско­рение свободного падения g выражено в м/с²)

(5.22)

где l_i и d_i — длина и диаметр трубы; — коэффициент местного сопротивления; v_i — средняя скорость потока в трубе; — коэффициент сопротивления трения; — приведенная длина трубы (учитывает местные сопротив­ления с помощью их эквивалентных длин ); , здесь .

Конкретный вид системы расчетных уравнений к способы ее решения определяются типом сложного трубо­провода и характером поставленной задачи. Для получе­ния однозначного решения система расчетных уравнений должна быть замкнутой, т. е. число независимых неиз­вестных в ней должно быть равно числу уравнений.