Манометрическое давление и вакуум

В открытых сосудах, водоемах абсолютным давлением окружающей среды является атмосферное давление р_а. Для этих слу­чаев уравнение (2.9) будет иметь вид:

Если абсолютное давление в данной точке жидкости больше атмосферного (р > р_a), то последний член уравнения (2.10) определяет манометрическое давление

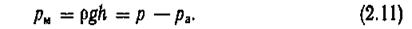Манометрическое давление представляет собой избыток давления в данной точке над атмосферным. Из уравнения (2.11) можно определить пределы изменения манометрического давления: при р = р_а ,p_m= 0, при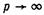

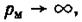т. е. значение манометрического давления может изме­няться от 0 до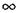

Если абсолютное давление в данной точке жидкости меньше атмосферного (р < р_а), то послед­ний член уравнения (2.10) опре­деляет вакуум, или разрежение,

Вакуум представляет собой не­достаток давления в данной точке до атмосферного.

Пределы изменения вакуума могут быть установлены из выражения (2.12): при р → 0 р_в→ р_а при р = р_а р_в = 0, т. е. значение вакуума может меняться от 0 до р_а.

Проиллюстрируем графически все сказанное выше о вакууме, манометрическом и абсолютном давлениях.

Представим себе плоскость, во всех точках которой абсолютное давление р = 0. След этой плоскости изображен на рис. 2.6 горизонтальной линией 00; А А - след плоскости, абсолютное да­вление во всех точках которой равно атмосферному р = р_а. Таким образом, линия 00 является базой для отсчета абсолютного давле­ния, а линия АА — базой для отсчета манометрического давления и вакуума.

Расстояние от точки С до линии 00 представляет собой абсолютное давление в этой точке p_с, а расстояние от точки С до линии АА — манометрическое давление в этой точке р_мС.

Аналогично расстояние от точки D до линии 00 представляет собой абсолютное давление в этой точке p_Dj а расстояние от точки D до линии АА — вакуум в этой точке р_BD.

Приведенная на рис. 2.6 схема дает также наглядное представление о пределах изменения манометрического давления и вакуума, которые были установлены выше из выражений (2.11) и (2.12).

Для измерения рассмотренных выше давлений применяют различные измерительные приборы, принцип действия и устройство которых рассмотрены в главе 9.

Закон Паскаля

Поместим на свободную поверхность жидкости, находящейся в равновесии в резервуаре (рис. 2.10, а), поршень и приложим к нему силу 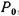, в результате чего со стороны поршня на жидкость возникает давление 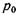. В соответствии с основным уравнением гидростатики (2.9) абсолютные давления в произвольно выбранных точках жидкости А, В, С будут соответственно равны:

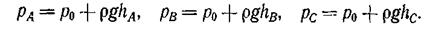
Из анализа полученных уравнений видно, что абсолютные давления в точках жидкости, находящихся на разной глубине, будут различные, однако внешнее давление на жидкость, заключенную в замкнутом сосуде, передается всем ее частицам без изменения. В этом суть закона Паскаля.

Практически закон Паскаля используется в ряде гидравлических машин: гидравлических прессах и подъемниках, объемных насосах и гидродвигателях (см. главы 10 и 14) и др.

На рис. 2.10, б приведена принципиальная схема гидравлического пресса. Прикладывая к меньшему поршню силу 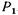, создаем в жидкости давление

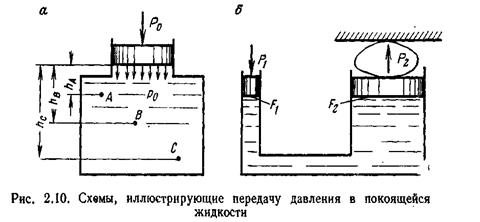
P=P₁:F₁ которое в соответствии с законом Паскаля передается большему поршню, вызывая силу P₂ = pF₂. Если пренебречь сопротивлениями, то