Государственный комитет рыбного хозяйства украины

МИНИСТЕРСТВО АГРАРНОЙ ПОЛИТИКИ УКРАИНЫ

ГОСУДАРСТВЕННЫЙ КОМИТЕТ РЫБНОГО ХОЗЯЙСТВА УКРАИНЫ

КЕРЧЕНСКИЙ ГОСУДАРСТВЕННЫЙ МОРСКОЙ ТЕХНОЛОГИЧЕСКИЙ

УНИВЕРСИТЕТ

Кафедра «Эксплуатация судовых энергетических установок»

ГИДРОМЕХАНИКА

КОНСПЕКТ ЛЕКЦИЙ

для студентов направления

6.070104 «Морской и речной транспорт»

специальности «Эксплуатация судовых

энергетических установок»

дневной и заочной форм обучения

Керчь, 2009

Автор – Осовский Д.И. к.т.н. доц. кафедры СЭУ КГМТУ.

Рецензент – к.т.н. доцент кафедры СЭУ КГМТУ Конюков В.Л., директор ООО «Сифопродукт» Худолей М.В.

Конспект лекций рассмотрен и одобрен на заседании кафедры СЭУ КГМТУ,

протокол № 1 от 31.08.2009 г.

Конспект лекций рассмотрен и рекомендован к утверждению на

заседании методической комиссии МФ КГМТУ,

протокол № 1 от 02.10.2009 г.

Методические указания утверждены на заседании Методического совета КГМТУ,

протокол № 1 от 15.10.2009 г.

© Керченский государственный морской технологический университет

ОГЛАВЛЕНИЕ.

Введение…………………………………………………………………….……….5

ГИДРАВЛИКА

Глава 1. Общие сведения о жидкости………………………………......................5

Тема 1.1. Основные определения и физические свойства жидкости………….5

Глава 2. Гидростатика. ……………………………………………………………12

Тема 2.1. Гидростатическое давление и его свойства………….……………...... 12

Тема 2.2. Взаимодействие покоящейся жидкости с твердой поверхностью……13

Тема 2.3. Плавание тел в жидкости…………..…………………………................13

Глава 3. Кинематика и динамика идеальной жидкости…………………………31

Тема 3.1. Кинематика и динамика идеальной жидкости……………………...….31

Тема 3.2. Вихревое движение жидкости………………………………………......31

Тема 3.3. Виды движения…………………………………………………………..33

Тема 3.4. Дифференциальные уравнения движения и баланса энергии для невязкой жидкости……………………………………………………………… … 43

Тема 3.5.Уравнение Бернулли для элементарной струйки невязкой жидкости..46

Тема 3.6. Энергетический и гидравлический смысл уравнения Бернулли….47

Тема 3.7.Уравнение Бернулли для газов при переменной плотности………….50

Тема 3.8.Уравнение Бернулли для элементарной струйки и потока вязкой жидкости. Рассеивание энергии, потери напора………………………………..........52

Тема 3.10. Поправочный коэффициент к скоростному напору………………..53

Тема 3.11. Мощность потока…………………………………………………….55

Тема 3.12. Применение уравнения Бернулли для решения задач………………55

Тема 3.13. Гидравлическое уравнение количества движения (Уравнение импульсов)…………………………………………………………………………….57

Тема 3.14. Ламинарный режим движения………………………………………..59

Тема 3.15. Закон распределения скоростей по сечению……………………….. 59

Тема 3.16. Расход и средняя скорость потока. Коэффициент Кориолиса……... 60

Тема 3.17. Закон гидравлического сопротивления. Коэффициент Дарси…….. 62

Раздел 4. Динамика реальной жидкости………………………………………… 64

Тема 4.1. Динамика реальной жидкости………………………………………… 64

Тема 4.2. Общие сведения о режимах движения жидкос­ти…………………..... 65

Тема 4.3. Ламинарное течение жидкости в круглых трубах……………............ 66

Тема 4.4. Турбулентное течение жидкости в трубах………………………….... 83

Тема 4.5. Местные гидравлические сопротивления……………………………. 85

Тема 4.6. Истечение жидкости через отверстия и насадки……….……………. 91

Тема 4.7. Кавитационное течение………………………………………..……....101

Тема 4.8. Неустановившееся движение жидкости………………………..…….103

Глава 5. Гидравлический расчет трубопроводов………………………………..104

Тема 5.1. Основное расчетное уравнение простого трубопровода.................….104

Тема 5.2. Расчет простых и сложных трубопроводов………...…………….…..110

Глава 6. Общие вопросы гидромеханики……………………………………….121

Тема 6.1. Основы теории гидродинамического подобия…………..……...…....121

Тема 6.2. Взаимодействие потока жидкости с твердыми телами………...….…125

Введение

Главной целью курса "Гидромеханика " является получение сведений в области анализа и прогнозирования условий течения реальных жидких и газообразных сред в элементах судовых энергетических установок (СЭУ), теплообменных аппаратах, вентиляторах, насосах, гидравлических системах, гидро- и пневмоприводах. Задачами дисциплины является дать будущим специалистам знания в следующих направлениях: движения жидкостей и газов, определения сил гидростатического давления на плоские и криволинейные поверхности, остойчивости и условий плавания тел, определения параметров истечения газов и жидкостей через отверстия и насадки, методы теории подобия и моделирования явлений гидромеханики, характеристик трубопроводов, гидромашин и насосов.

В результате изучения данной дисциплины студент получит знания:

- об основных физических свойствах жидкости,

- режимах движения жидкости,

- о теории ламинарного и турбулентного режима движения жидкости.

Каким образом происходит истечение жидкости через отверстия и насадки. Как производится гидравлический расчет трубопроводов. Получит понятие по теории гидравлического подобия. Устройство насосов, гидравлических приводов, устройств управления потоками жидкости.

После получения необходимых знаний, студент сможет проводить инженерные расчеты параметров трубопроводов машин и агрегатов, определять режим течения жидкости и рассчитывать потери давления в трубопроводах и на запорнорегулирующей арматуре. Уметь рассчитывать параметры любой гидравлической и воздушной системы и дать анализ ее работоспособности.

Кроме того, курс " Гидромеханика " необходим при изучении таких дисциплин, как "Судовые вспомогательные и промысловые меха­низмы, системы и их эксплуатация", "Судовые паровые и газовые тур­бины и их эксплуатация", "Судовые двигатели внутреннего сгорания и их эксплуатация" и др.

Изучать курс целесообразно по темам, руководствуясь настоя­щими методическими указаниями. Сначала следует изучить теоретичес­кую часть раздела, проанализировать приведенные здесь примеры и задачи с решениями. При этом вести краткий конс­пект, отражая в нем формулировки законов, выводы формул. Затем не­обходимо ответить на вопросы для самоподготовки, которые приведены в конце каждой темы.

ГИДРАВЛИКА

ГЛАВА 1 ОБЩИЕ СВЕДЕНИЯ О ЖИДКОСТИ

1.1 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТИ

Жидкостью называется непрерывная среда, обладающая свойством текучести.

Рассматриваемые в настоящем курсе жидкости можно разделить на две группы: капельные — практически несжимаемые (вода, спирт, ртуть, масла) и газообразные — легко сжимаемые (воздух и другие газы). Характерным различием этих жидкостей является также наличие у капельных жидкостей и отсутствие у газов свободной поверхности — поверхности раздела между жидкостью и газообразной средой.

Плотность представляет собой массу однородного вещества в единице объема

Размерность Единицей плотности в системе
СИ является килограмм на кубический метр (кг/м³). Значения
плотности некоторых жидкостей приведены в приложениях 1 и 2.

Иногда в справочниках вместо плотности приводятся значе­ния относительной плотности различных веществ.

Относительная плотность — безразмерная величина, представляющая собой отношение плотности рассматриваемого веще­ства к плотности стандартного вещества в определенных физических условиях

В качестве стандартного вещества при определении относительной плотности принимают: для твердых тел и капельных жидкостей — дистиллированную воду при температуре 277 К (4° С) и давлении 401 325 Па, имеющую плотность для газов — атмосферный воздух при стандартных условиях: температуре 293 К (20° С), давлении 101 325 Па и относительной влажности 50%, имеющий плотность

Для непосредственного измерения плотности капельных жидкостей в технике часто используют приборы, называемые ареометрами.

Сжимаемость — свойство жидкости изменять свою плотность при изменении давления и (или) температуры.

Плотность капельных жидкостей при температуре и давлении, отличных от начальных, может быть найдена из выражения

где — плотность жидкости при начальных температуре и давлении;

— приращения температуры и давления;

— коэффициенты температурного расширения и объемного сжатия, представляющие собой относительное изменение объема жидкости при изменении температуры или давления на одну единицу:

Величина, обратная ,β_ρ называется модулем упругости жидкости Значения коэффициентов весьма малы. Так, например, в интервале давлений Па при средние значения составляют: для воды Па^-1; для минеральных масел, при­меняемых в гидроприводах,

Поэтому при решении большинства практических задач изменением плотности капельных жидкостей при изменении температуры или давления обычно пренебрегают (исключение составляют задачи о гидравлическом ударе, об устойчивости и колебании гидравлических систем и некоторые другие, где приходится учитывать сжимаемость жидкости).

В отличие от капельных жидкостей плотность газов в сильной степени зависит от температуры и давления. Рассмотрим уравнение Клапейрона — Менделеева

где р — абсолютное давление; - объем; - масса;

m - молярная масса; - универсальная газовая постоянная (R=8,314 Дж/(моль^. К)

Т - абсолютная температура; u=V/m - удельный объем;

газовая постоянная (для воздуха R=287Дж/(кг^.К), для метана R=287Дж/(кг^.К),

Из этих уравнений можно установить зависимость плотности газа от температуры и давления

где r и r₀ — плотности газа соответственно при новых давлении
и температуре и начальных давлении и температуре

Оценить сжимаемость жидкостей можно и другим образом. Так, в состоянии покоя характерным параметром сжимаемости жидкости является скорость распространения в ней звуковых колебаний (скорость звука

где - приращение давления; — приращение плотности жидкости.

Чем больше скорость звука, тем меньше сжимаемость данной жидкости, и наоборот.

Для оценки сжимаемости движущейся жидкости пользуются обычно не абсолютным значением скорости звука, а отношением скорости потока v к скорости звука, а в данной жидкости, которое называется числом Маха,

Если скорость движения жидкости мала по сравнению со ско­ростью распространения в ней звука, т. е. число Маха значительно меньше единицы, то независимо от абсолютного значения скорости звука капельную жидкость (или газ) при таком движении можно считать практически несжимаемой.

При повышении температуры или снижении давления капельной жидкости до определенных значений, когда давление станет меньше или равно давлению насыщенных паров этой жидкости при данной температуре , внутри жидкости начинают образовываться пузырьки и даже целые полости, заполненные парами данной жидкости и растворенными в ней газами, которые нарушают сплошность капельной жидкости. Таким образом, законы, установленные для сплошных сред, в этих случаях неприменимы.

Таблица 1.1

Давление (упругость) насыщенных паров некоторых жидкостей при различных температурах (р_н. _ш кПа)

При наличии в жидкости свободной поверхности эти пузырьки всплывают и выходят через нее, т. е. происходит кипение жидкости. Если капельная жидкость находится в замкнутом пространстве и не имеет свободной поверхности, то эти пузырьки или полости, перемещаясь в массе жидкости или вместе с ней и попадая в области с более низкой температурой или более высоким давлением, почти мгновенно (за несколько миллисекунд) смыкаются (так как пары конденсируются, а газы снова растворяются в жид­кости и в образовавшиеся пустоты с большими скоростями устремляются частицы жидкости), что приводит к резкому повышению давления в этих местах, а также к местному повышению температуры. Это явление называется кавитацией.

Кавитация в трубопроводах и гидравлических машинах является крайне вредной, так как многократное местное повышение давления, сопровождающееся ударами частиц жидкости о стенки труб и проточных элементов гидромашин, приводят к их эрозии.

Капиллярность — способность капельной жидкости в трубках малого диаметра подниматься выше свободной поверхности в резервуаре, образуя вогнутый мениск (если жидкость смачивает стенки трубки), или опускаться ниже свободной поверхности, образуя выпуклый мениск (если жидкость не смачивает стенки трубки). Эта способность обусловлена поверхностным натяжением жидкости и молекулярными силами взаимодействия между жидкостями.

Рис, 1.1. Относительное движение слоев жидкости.

Высота h поднятия или опускания жидкости в трубке может быть вычислена по формуле

где — поверхностное натяжение; — плотность жидкости; — диаметр трубки; — постоянная для данной жидкости.

При подстановке в формулу (1.8) d в миллиметрах значения k можно принимать равными: для воды +30 мм², для спирта + 11 мм², для ртути — 10 мм² .

Вязкость - свойство жидкости оказывать сопротивление относительному движению (сдвигу) частиц жидкости.

При движении реальной жидкости вследствие ее вязкости между соседними слоями жидкости, а также жидкостью и стенками русла возникают силы внутреннего трения и вызванные ими касательные напряжения, направленные в сторону, противоположную движению, что приводит к различию скоростей частиц в разных слоях потока и их деформации (сдвигу).

Если представить поток состоящим из отдельных слоев бесконечно малой толщины (рис. 1.1), то скорости этих слоев будут изменяться по некоторому закону от нуля (у стенки) до максимума (в центре потока). Пусть скорости соседних слоев будут u и u+du. В прямолинейном движении du можно рассматривать как скорость деформации, а градиент скорости как угловую скорость деформации.

Согласно гипотезе И. Ньютона, высказанной им в 1686г., а затем экспериментально и теоретически обоснованной в 1883 г.проф. Н. П. Петровым, сила внутреннего трения , возникающая между двумя слоями движущейся прямолинейно жидкости, прямопропорциональна поверхности соприкасающихся слоев , градиенту скорости du/dy , зависит от рода жидкости и температуры и не зависит от давления ¹

где m - динамическая вязкость.

Жидкости, в которых силы внутреннего трения не подчиняются уравнению (1.9), называются аномальными или неньютоновскими. К ним относятся некоторые масла при отрицательных температурах, коллоиды, парафинистые нефтепродукты при низких температурах. Вода, воздух, спирт, ртуть, большинство масел, приме­няемых в гидроприводах, и другие относятся к обычным, т. е. ньютоновским жидкостям.

Разделив обе части уравнения (1.9) на получим касательное напряжение (напряжение силы трения)

Так как T и t всегда положительны, то в уравнениях (1.9)и (1.10) должен быть поставлен знак плюс, если du/dy положительно, и знак минус, если du/dy отрицательно.

Из уравнения (1.10) следует, что динамическая вязкость m =t :(du/dy) численно равна касательному напряжению при градиенте скорости , равном едини-

це, т. е. имеет вполне определенный физический смысл и полностью характеризует вязкость жидкости.

Размерность , Единицей динамической вязкости в системе СИ является паскаль-секунда (Па*с). Широко применялась также единица системы СГС — пуаз (П = дин *с/см²); 1 П =0,1 Па-с.

При выполнении технических расчетов в гидравлике обычно пользуются кинематической вязкостью v, представляющей собой отношение динамической вязкости жидкости к ее плотности

Размерность Единицей кинематической вязкости в системе СИ является метр в квадрате на секунду (м²/с)².

Широко применялась также единица системы СГС — сантиметр в квадрате на секунду, называвшаяся стокс (см^а/с = Ст), а также ее производная — сантистокс (сСт); 1 м^а/с = 10⁴ Ст = 10^е сСт. В соответствии с СТ СЭВ 1052—78 такие единицы вязкости, как пуаз, стокс, сантистокс в настоящее время не применяются.

Для определения вязкости жидкостей используют приборы, называемые вискозиметрами. Для измерения вязкости жидкостей более вязких, чем вода (масел, нефтепродуктов) применяют обычно вискозиметр (рис. 1.2), состоящий из двух сосудов, пространство между которыми заполняется водой для поддержания требуемой температуры. К сферическому дну внутреннего сосуда прикреплена трубочка с внутренним диаметром .около 3 мм, отверстие в которой нормально закрыто клапаном.

Во внутренний сосуд до определенного уровня наливается ис­пытуемая жидкость и с помощью нагревательного устройства темпе­ратура ее доводится до требуемого значения t', фиксируемого термометром, после чего клапан открывается и с помощью секундомера измеряется время истечения 200 см³ этой жидкости. Аналогичный опыт произво­дят с дистиллированной водой при t = 20° С. Отношение измеренных времен истечения испытуемой жидкости Т_и,ж и дистиллированной воды Т_д,п составляет число градусов условной вязкости (или градусов Энглера):

Для перевода градусов условной вязкости в единицы системы СИ (м²/с) пользуются эмпирической формулой Уббелоде

Вязкость зависит от рода жидкости, ее температуры и давле­ния. Значения вязкости некоторых жидкостей в различных единицах приведены в приложениях 1 и 2.

С увеличением температуры вязкость капельных жидкостей уменьшается, а газообразных — увеличивается. Зависимость вязкости от температуры для разных жидкостей различна и выразить ее аналитически общим уравнением не представляется возможным.

При выполнении расчетов можно воспользоваться следующими зависимостями (м⁸/с): для воздуха

Для минеральных масел, применяемых в гидроприводах в интервале температур 30—150° С и при вязкости до 10°C

где - кинематическая вязкость соответственно при данной температуре и при 50° С;

t — температура, °С;

n - показатель степени, значение которого в зависимости от °ВУ составляет

Характер изменения вязкости жидкостей при изменении давления различен и зависит от начальной вязкости и температуры. Для большинства капельных жидкостей с повышением давления вязкость несколько увеличивается.

Вязкость минеральных масел в пределах давлений 0—50 МПа изменяется практически линейно и может быть вычислена по формуле

где v_p и v₀ - кинематическая вязкость соответственно при давлении р и атмосферном давлении;

k_p - опытный коэффициент (при расчетах систем гидроприводов в пределах указанных давлений принимается равным 0,03);

p - давление, при котором определяется вязкость, МПа.

Вопросы для самопроверки.

1.В чем состоит отличие жидкостей от твердых тел и газов?

2.Какова взаимосвязь между плотностью и удельным весом?

3.Как изменяется плотность жидкости при увеличении давления
и температуры?

4.Какова связь между коэффициентом объемного сжатия и объемным модулем упругости?

5.Что представляет собой коэффициент температурного расшире­ния?

6.Что называется вязкостью? В чем состоит закон жидкостного
трения Ньютона?

7.Какова связь между динамическим и кинематическим коэффициентами вязкости?

8. Чем отличается идеальная жидкость от реальной?

9. Что называется давлением насыщенных паров жидкости и от чего оно зависит?

10. Что такое поверхностное натяжение и от чего оно зависит?

ГЛАВА 2 ГИДРОСТАТИКА

С твердой поверхностью

Силы давления жидкости на плоские и криволинейные поверхности. Эпюры давления. Центр тяжести и центр давления. Определение равнодействующей сил давления на плоскую и криволинейную поверхности. Тело давления. Равновесие жидкости в движущихся сосудах.

Закон Паскаля

Поместим на свободную поверхность жидкости, находящейся в равновесии в резервуаре (рис. 2.10, а), поршень и приложим к нему силу 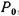, в результате чего со стороны поршня на жидкость возникает давление 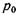. В соответствии с основным уравнением гидростатики (2.9) абсолютные давления в произвольно выбранных точках жидкости А, В, С будут соответственно равны:

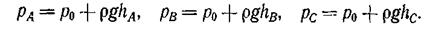
Из анализа полученных уравнений видно, что абсолютные давления в точках жидкости, находящихся на разной глубине, будут различные, однако внешнее давление на жидкость, заключенную в замкнутом сосуде, передается всем ее частицам без изменения. В этом суть закона Паскаля.

Практически закон Паскаля используется в ряде гидравлических машин: гидравлических прессах и подъемниках, объемных насосах и гидродвигателях (см. главы 10 и 14) и др.

На рис. 2.10, б приведена принципиальная схема гидравлического пресса. Прикладывая к меньшему поршню силу 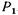, создаем в жидкости давление

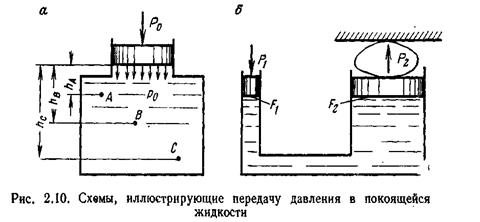
P=P₁:F₁ которое в соответствии с законом Паскаля передается большему поршню, вызывая силу P₂ = pF₂. Если пренебречь сопротивлениями, то

Закон Архимеда

Сила, с которой жидкость воздействует на погруженное в нее тело, равна весу жидкости в объеме погруженного тела. Плавучесть тела определяется условиями его равновесия на свободной поверхности.

Плавающее тело при качке может наклоняться в одну и в другую сторону или, как обычно говорят, давать крен. Способность судна выходить из крена в первоначальное положение называется остойчивостью судна.

Метацентром называют точку пересечения оси плавания с линией действия архимедовой силы при крене плавающего тела или судна. Метацентрической высотой называют превышение метацентра над центром тяжести тела. Для остойчивости судна или тела надо иметь положительное значение метацентрической высоты.Рассмотрим погруженное в покоящуюся жидкость твердое тело произвольной формы, объем которого V (рис. 2.16). В соответствии 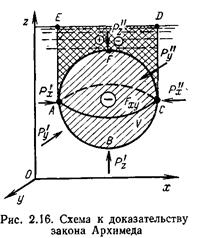с уравнением (2.26) на поверхность этого тела со стороны жид­кости будет действовать сила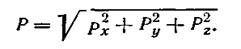

Если рассечь тело вертикальными плоскостями, параллель­ными плоскостям xOz и yOz, таким образом, чтобы площади сечений получились максимальными, то нетрудно показать, что горизонтальные составляющие Р_х и Р_у равны нулю, так как на каждую из частей будут действовать равные и противоположно направленные силы:

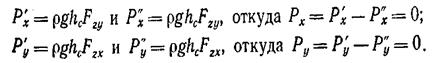
Вертикальная составляющая силы давления жидкости на тело

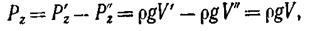
Где V’- объем ABCDEA, 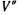— объем AFCDEA, 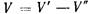результирующий объем тела давления, равный в данном случае объему погруженного в жидкость тела (объему ABCFA) и являющийся фиктивным. '

Подставляя в уравнение (2.26) значения 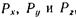, получим

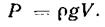(2.31)

На погруженное в жидкость тело действует архимедова сила, направленная вертикально вверх и равная силе тяжести жидкости в объеме погруженной части тела. Это и есть закон Архимеда, открытый им в 250 году до н. э.

В уравнении (2.31): Р—архимедова сила, V—объемное водоизмещение (объем вытесненной телом жидкости), 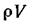—водоизмещение (масса вытесненной телом жидкости).

Тело, погруженное в покоящуюся жидкость, находится под действием двух сил: силы тяжести 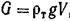, приложенной в центре тяжести тела, и архимедовой силы 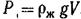, приложенной в центре объемного водоизмещения. В этих формулах: 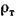— плотность тела, 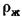— плотность жидкости.

При погружении тела в жидкость может быть три характерных случая:

1. 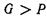, т. е. сила тяжести тела больше архимедовой силы в этом случае их результирующая 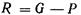будет направлена вниз, следовательно, тело тонет.

2. 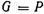, т. е. сила тяжести тела равна архимедовой силе; в этом случае их результирующая 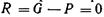, следовательно тело будет находиться в жидкости в состоянии безразличного равновесия (подводное плавание).

3. 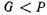, т. е. сила тяжести тела меньше архимедовой силы в этом случае их результирующая 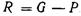будет направлена вверх, следовательно, тело всплывает.

В последнем случае при выходе части тела из жидкости архимедова сила уменьшается и в определенный момент наступит равновесие 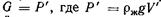(надводное плавание). Объем погруженной части плавающего на поверхности жидкости тела может быть найден по формуле

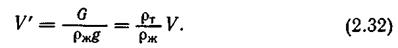
Для равновесия тела при подводном или надводном плавании помимо равенства сил 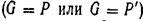необходимо еще равенство нулю суммарного момента. Последнее условие соблюдается тогда, когда центр тяжести тела лежит на одной плоскости с центром водоизмещения. Более подробно вопросы плавания тел и устойчивости их равновесия рассматриваются в специальных курсах.

Закон Архимеда широко используется при расчете и проектировании судов и других плавающих средств, различных поплав­ковых устройств (датчиков уровня, дифманометрев поплавкового типа), в гравитационных методах обогащения полезных ископа­емых и т. д.

Вопросы для самопроверки

1. Что называют гидростатическим давлением? В каких единицах его выражают? Каковы свойства гидростатического давления?

2. Что называют избыточным, абсолютным давлением, вакуумом?
Чему равна наибольшая величина вакуума?

3. Объясните физический смысл величин, входящих в дифференциальные уравнения равновесия жидкости Эйлера?

4. В чем разница между напором и давлением?

5. Что такое поверхность равного давления? Каковы ее формы
и уравнения при абсолютном покое, в случае движения сосуда вокруг
вертикальной оси?

6. Как формулируется закон Паскаля и какова его связь с основным уравнением гидростатики?

7. Почему центр давления находится ниже центра тяжести смо­ченной поверхности наклонной плоскости стенки?

8. Какие правила следует соблюдать при вычерчивании тела давления?

9. Сформулируйте закон Архимеда и напишите условия плавания тел.

10. Что такое плавучесть и остойчивость судна?

11. Дайте определения понятиям: метацентр, метацентрическая
высота, метацентрический радиус, водоизмещение.

12. Изложите условия статической остойчивости судна.

Способы описания движения

Движущаяся жидкость представляет сплошную среду сово­купности частиц, которые перемещаются с различными параме­трами, изменяющимися в зависимости от координат и времени.

Частица сплошной среды — это весьма малый элемент объема среды (элементарный объем), который можно считать точечным. В кинематике жидкости возможны два способа описания движения — Лагранжа и Эйлера.

По способу Лагранжа движение жидкости задается путем указания зависимости координат определенной (намеченной) частицы жидкости от времени. Движущаяся частица жидкости описывает в пространстве траекторию, вдоль которой изменяется скорость.

На рис. 3.1, а показана траектория движения частицы А в неподвижной системе координат, где за определенное время координаты частицы изменялись с х₀, z₀ на x_lt z₁ за время t₁ ; х₂, z₂ за время t_z и т. д. Таким образом, при описании движения пере­менными являются скорость, ускорение и координаты частицы. Практически для большинства инженерных задач нет необходи­мости в знании параметров движения отдельных частиц, поэтому способ Лагранжа применяется только в особых случаях: например, Для описания переноса жидкостью мельчайших твердых частиц (ила).

Способ Эйлера заключается в том, что движение определяется полем скоростей жидкости в пространстве в каждый момент времени, т. е. описывается движение различных частиц, проходящих через намеченные точки пространства, заполненного жидкостью. При этом переменными являются скорости частиц, а координаты точки пространства, через которые проходят частицы, остаются постоянными (известными). На рис. 3.1, б показаны зафиксированные точки 1, 2, 3 в пространстве, через которые в разное время t₁ , t₂ проходят частицы co скоростями u₁(t₁), u₂(t₁), u₃(t₁), u₁(t₂),u₂(t₂),u₃(t₂).

Последнее обстоятельство значительно облегчает проведение теоретических и экспериментальных исследований, так как координаты зафиксированных точек в пространстве известны и постоянны.

При решении большинства инженерных задач необходимо знать, с какими скоростями различные частицы жидкости про­ходят через определенные элементы конструкций или инженерных сооружений или подходят к ним. Поэтому способ описания движения Эйлера принят основным.

По Эйлеру задано поле скоростей жидкости в пространстве в каждый момент времени в проекциях скорости и на оси непо­движной прямоугольной декартовой системы координат:

Проекции ускорений элементарных объемов среды в этой системе координат по правилу дифференцирования сложной функции будут:

Зная, что являются проекциями скорости и в

момент времени t, и подставляя их в уравне­ния проекций ускорений, получим:

Рассмотрим кинематический смысл каждого слагаемого в правой части системы уравнений (3,2).

Последние слагаемые du/dt представляют проекции локального ускорения, которое обусловливается изменением поля скоростей со временем при фиксированных координатах, т. е. местным локальным изменением.

Первые три слагаемые в правой части (3.2) дают проекции конвективного ускорения, которое образуется за счет изменения координат частицы, соответствующих ее передвижению (конвекции).

Конвективное ускорение возможно только при движении жидкости и газов.

ВИДЫ ДВИЖЕНИЯ

Вихревое движение

Движению жидкости часто сопутствует вихревое движение, вызванное вращением элементарного объема. Угловая скорость вра­щения со элементарного объема жидкости называется вихрем, а линия, касательная во всех точках к векторам вихря вихревой линией (рис. 3.4, а).

Поверхность, образованная вихревыми линиями, проведенными через все точки элементарного замкнутого контура, называют вихревой трубкой, а жидкость, заключенную внутри вихревой трубки, — вихревой нитью — шнуром (рис. 3.4, б).

Расчетным вихрем является вектор угловой скорости вращения частиц относительно мгновенной оси. Физический вихрь — группа частиц, вращающихся как твердое тело вокруг некоторой мгновенной оси. Мгновенная ось вращения может быть неподвижной или перемещающейся в пространстве. Перемещающиеся вихри наблюдаются сзади какого-либо тела, движущегося в жидкости, в виде колец дыма и пара, выходящих из труб. В природе они часто встречаются в виде смерчей. Изучение перемещающихся вихрей имеет большое значение при конструировании и исследовании лопастных машин, самолетов и при транспортировании жидкостью твердых тел. В гидромеханике широко п