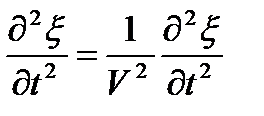Свободные гармонические колебания в колебательном контуре
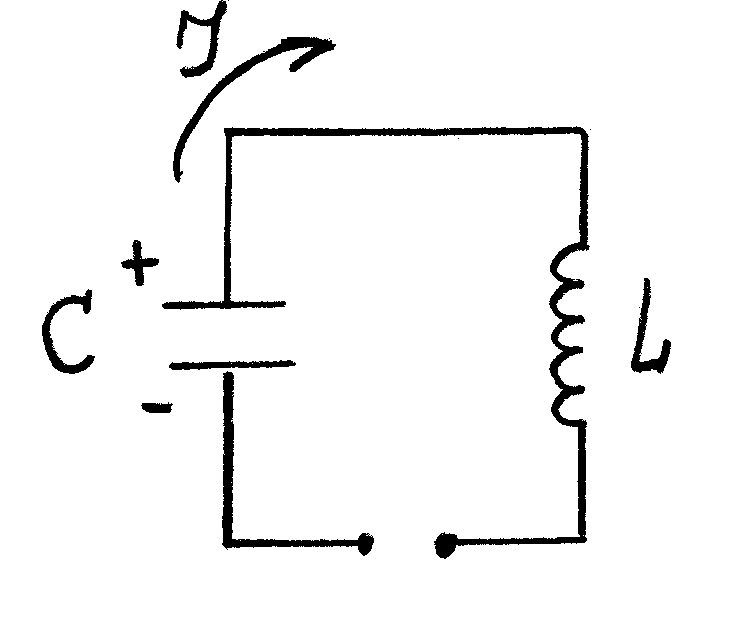
Рассмотрим идеальный колебательный контур
(R = 0).
; 
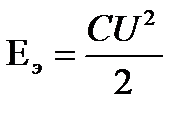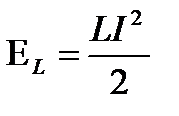
Полная энергия:
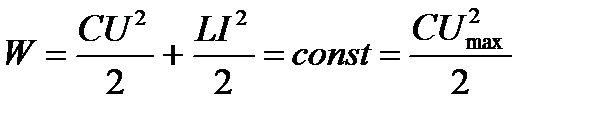
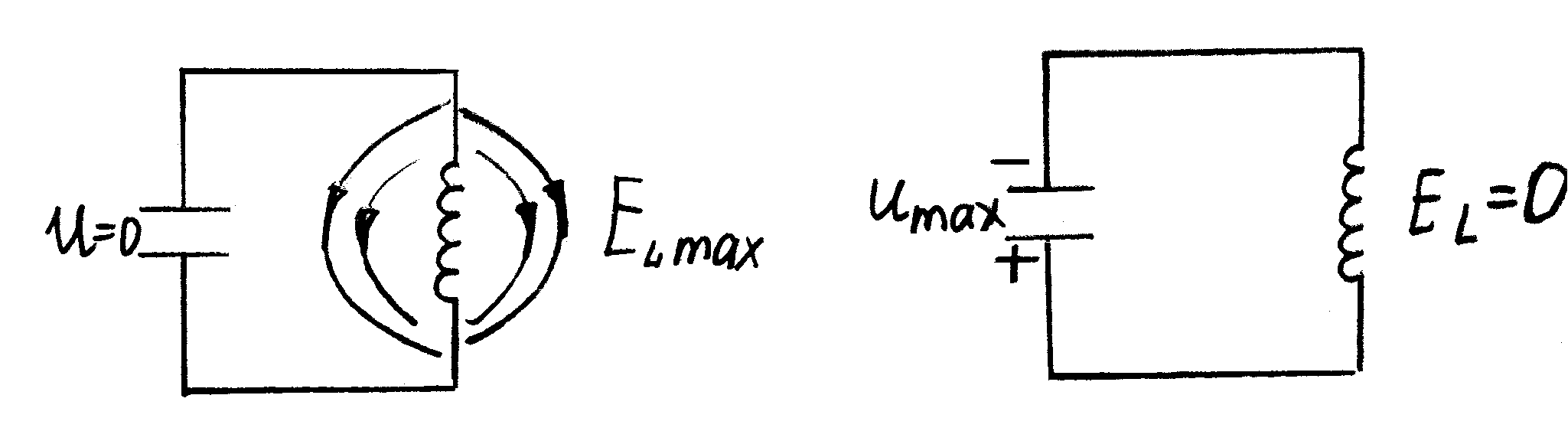
В контуре возникают электромагнитные колебания. Процесс связан не только с колебаниями величины заряда, но и с перекачкой энергии из электрического поля в магнитное и наоборот.
В любой момент времени разность потенциалов на обкладках конденсатора равна ЭДС самоиндукции.
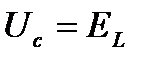
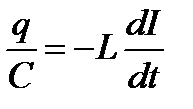
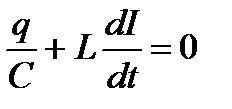
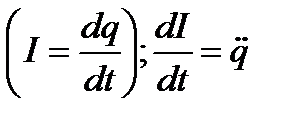
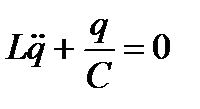
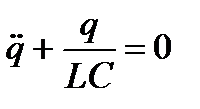- дифференциальное уравнение гармонических
электромагнитных колебаний
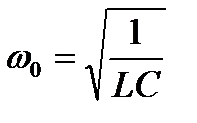
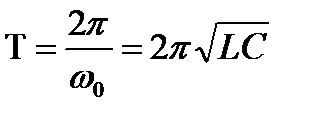- формула Томсона
Сила тока в колебательном контуре (в катушке)
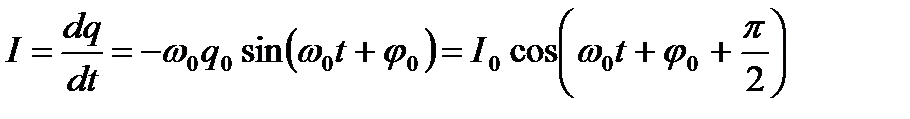
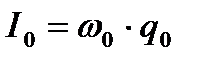- амплитуда тока
Напряжение в конденсаторе
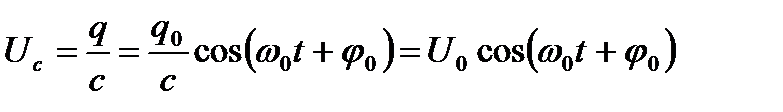
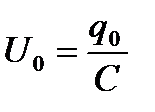- амплитуда напряжения
Затухающие колебания в колебательном контуре.
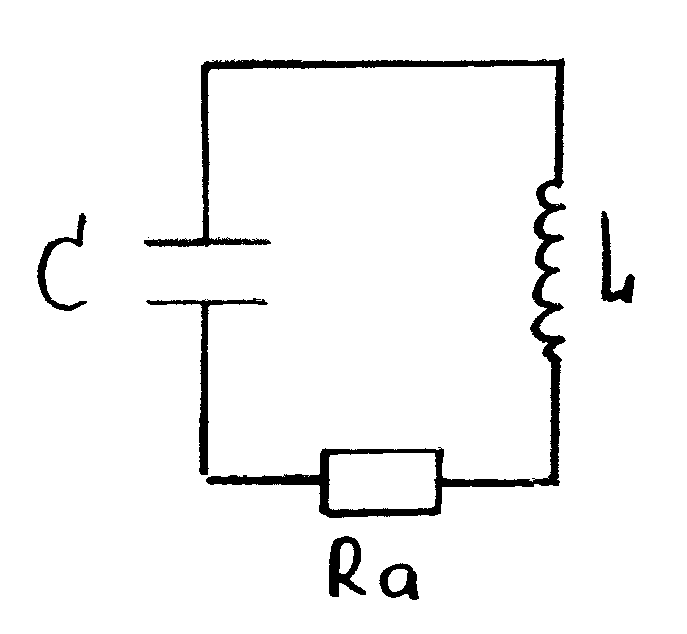По закону Ома для контура:
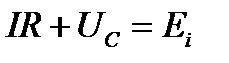
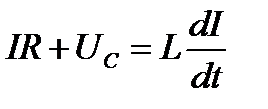
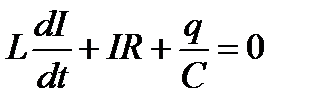
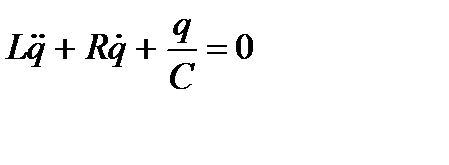
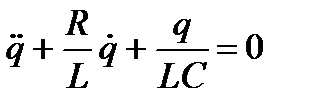- дифференциальное уравнение затухающих колебаний
п заряда в колебательном контуре.
; 
;
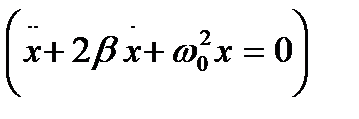
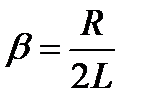
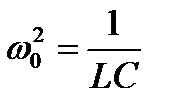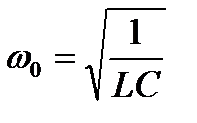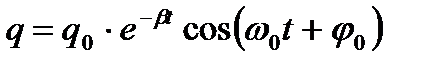- уравнение колебаний заряда
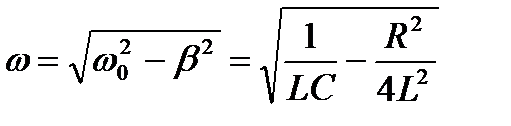-частота колебаний заряда ω меньше собственной частоты
колебательного контура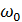 
; 
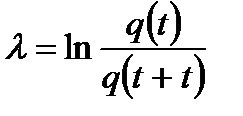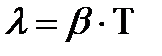
ВОЛНОВЫЕ ПРОЦЕССЫ
Волна – это процесс распространения колебаний в сплошной среде.
При распространении волны частицы среды не движутся вместе с волной, а совершают колебания около своих положений равновесия. Вместе с волной от частицы к частице передается лишь состояние колебательного движения и его энергия.
Основное свойство волн – перенос энергии без переноса вещества.
| ВОЛНЫ |
| Упругие (механические) |
| Электромагнитные |
| Продольные |
| Поперечные |
Продольные волны – частицы среды колеблются в направлении распространения волны.
Могут распространяться в средах, в которых возникают упругие силы при деформациях сжатия и растяжения, т. е. в твердых, жидких и газообразных телах.
Поперечные волны – частицы среды колеблются в плоскости, перпендикулярной направлению распространения волны.
Распространяются в среде, где возникают упругие силы при деформации сдвига, т. е. только в твердых телах.
Гармоническая упругая волна – если соответствующие ей колебания частиц среды являются гармоническими.
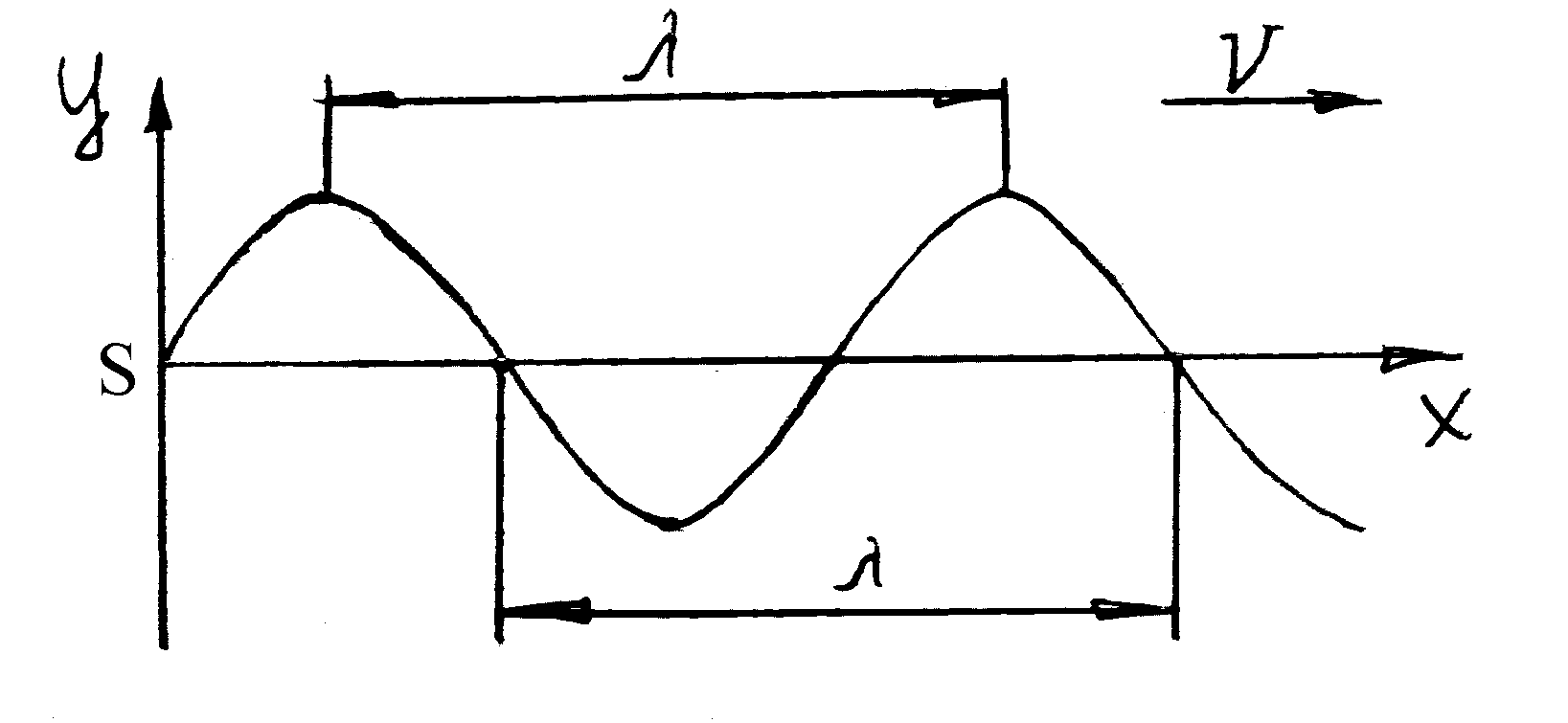
Закон колебаний точки S.
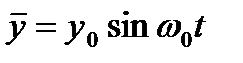
Длина волны - расстояние, на которое распространяется фаза колебаний за время равное периоду:
; 
; 
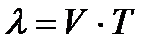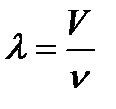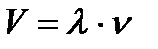
Волновая поверхность – геометрическое место точек, колеблющихся в одинаковой фазе.
Фронт волны – геометрическое место точек, до которых доходят колебания к моменту времени t.
Волновой фронт также является волновой поверхностью.
У плоской волны волновая поверхность – это совокупность плоскостей, параллельных друг другу.
У сферической волны – волновая поверхность - это совокупность сфер.
Уравнение бегущей волны. Фазовая скорость.
Волновое уравнение
1. Бегущая волна – это волна, которая переносит в пространстве энергию.
Перенос энергии количественно характеризуется вектором Умова (вектор плотности потока энергии). Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.
Уравнение бегущей волны, которая распространяется в прямом направлении:
Если плоская волна распространяется в противоположном направлении, то
В общем случае:
Где А – амплитуда волны;
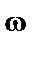- циклическая частота волны;
- фаза волны
Для волн в качестве основной характеристики используетсяволновое число:
Тогда уравнение бегущей волны.
Фазовая скорость.
Пусть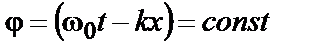 
, тогда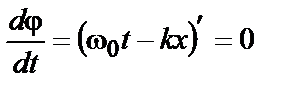 
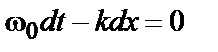
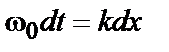
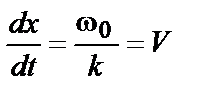
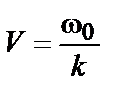- фазовая скорость.
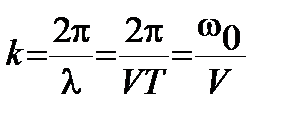– волновое число
3. Волновое уравнение – это дифференциальное уравнение волны:
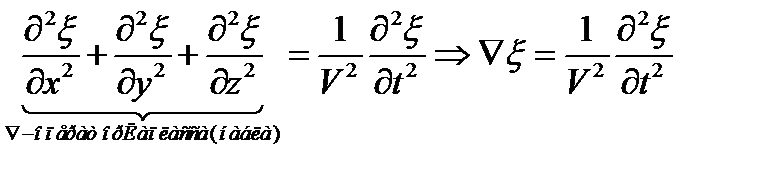
V – фазовая скорость.
Для плоской волны, распространяющейся вдоль оси Х:
