Форма фигуры Лиссажу зависит от соотношения амплитуд, частот и разности фаз.

Рассмотрим несколько примеров:

а) Сложение двух гармонических колебаний одинаковой частоты ω, которые осуществляются вдоль координат OXи OY и имеют разность фаз колебаний φ

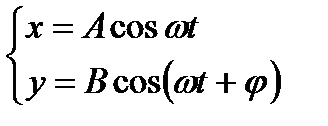
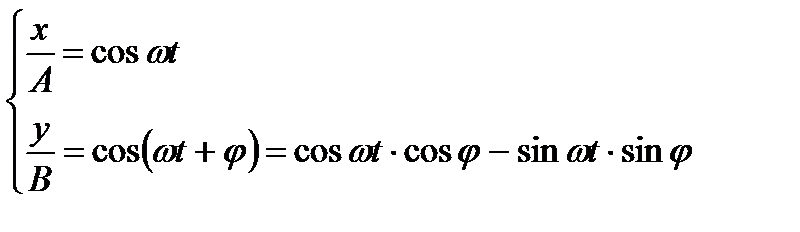
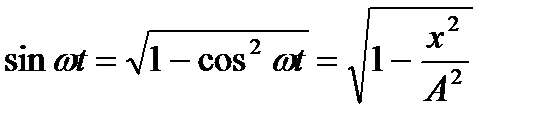
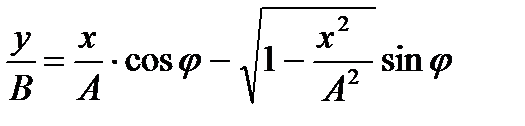
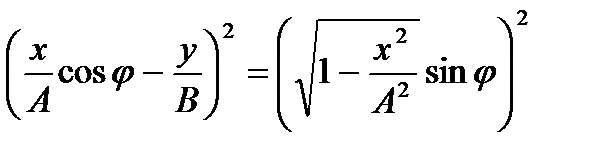
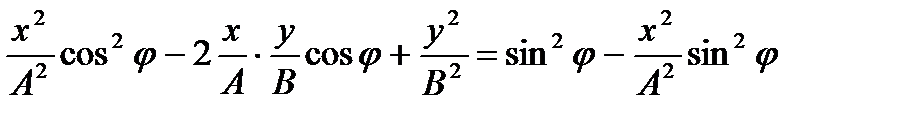
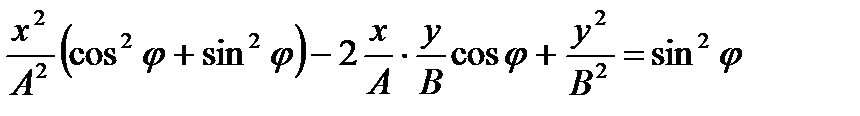
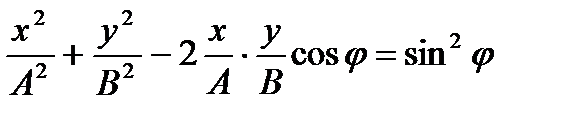- уравнение траектории движения точки.

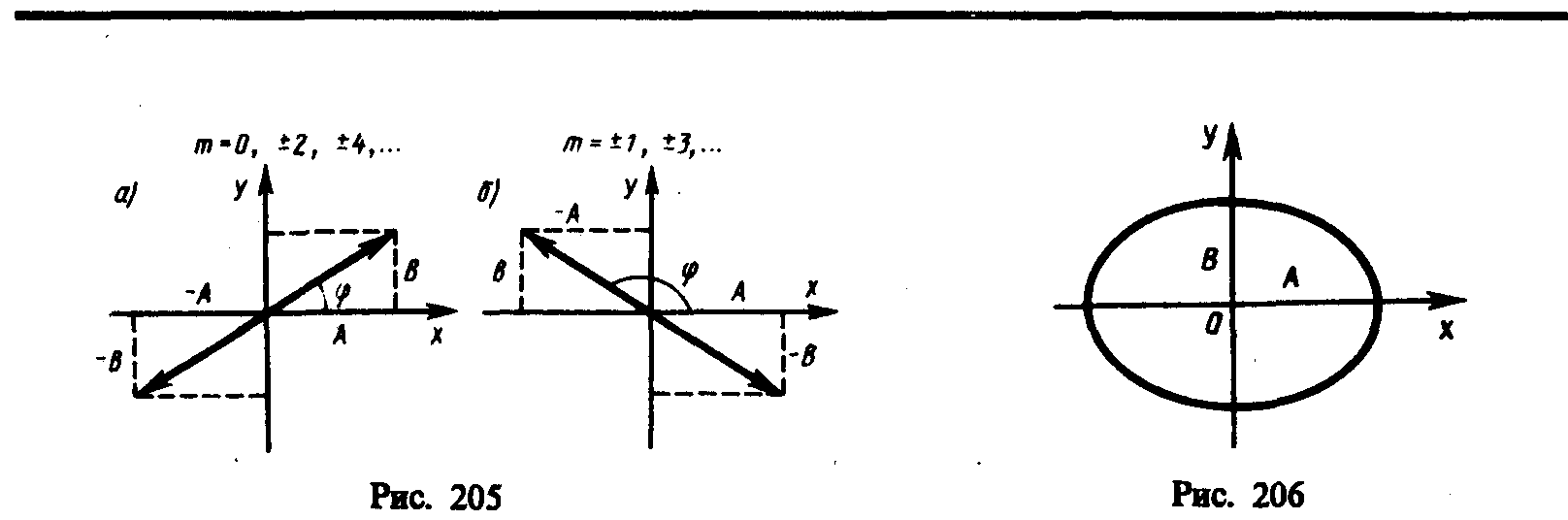
б) Сложение двух гармонических колебаний одинаковой частоты ω, которые осуществляются вдоль координат OXи OY и имеют разность фаз колебаний π/2

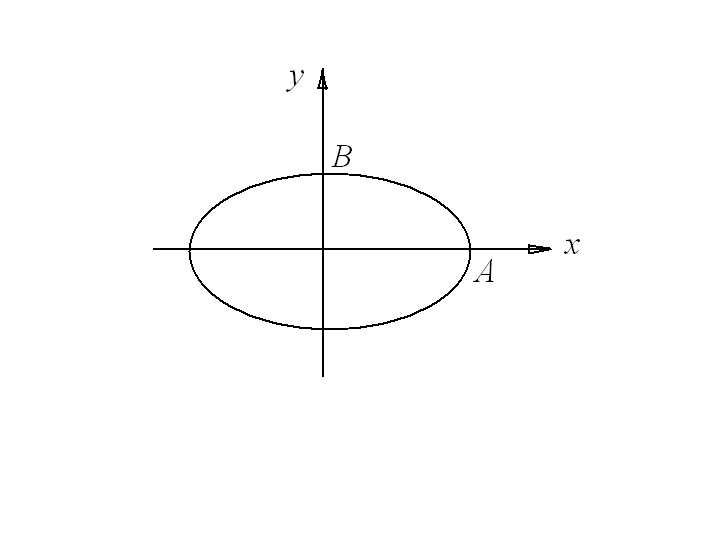
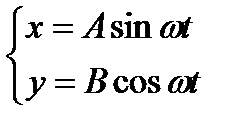отсюда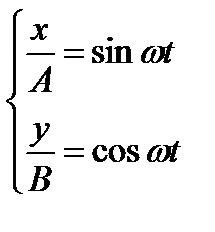

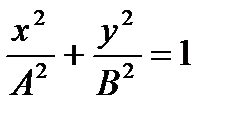- уравнение эллипса

Если амплитуды колебаний А и В одинаковые, то эллипс превращается в окружность

в) Сложение двух гармонических колебаний одинаковой частоты ω, которые осуществляются вдоль координат OXи OY и имеют разность фаз колебаний π

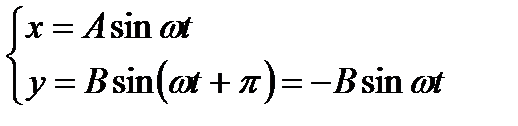
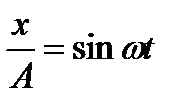
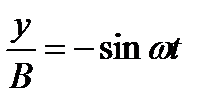
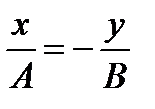
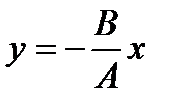- уравнение прямой

Результирующее колебание является гармоническим колебанием с частотой w и амплитудой 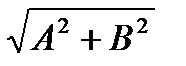, совершающимся вдоль прямой, составляющей с осью х угол j=arctg .

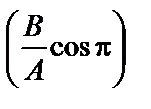Затухающие колебания

Это колебания, амплитуда которых со временем уменьшается

Дифференциальное уравнение затухающего колебания

.

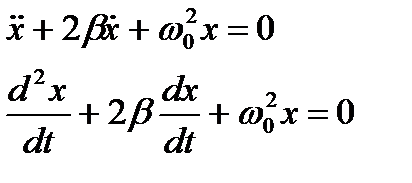Решением дифференциального уравнения является уравнение вида:

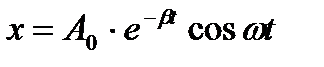
В общем случае уравнение затухающих колебанийможно записать в виде:

=

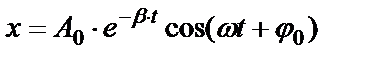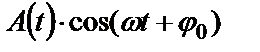
Амплитуда затухающих колебанийуменьшается со временем по экспоненциальной зависимости:

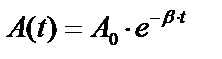
где A₀ - начальная амплитуда (характеризует максимальное отклонение параметра х в момент времени t=0)

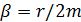– коэффициент затухания (характеризует скорость затухания

колебаний).

где r - коэффициент сопротивления; m - масса

T

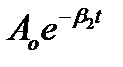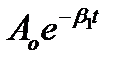хo

t

хo

t

х

Пунктирная линия на графике затухающих колебаний – это зависимость амплитуды от времени. Чем больше коэффициент затухания β (нижний рис ), тем больше скорость затухания колебаний

.

Логарифмический декремент затухания λ, который определяется как натуральный логарифм отношения амплитуды колебаний A(t) в момент времени t к амплитуде A(t+T) в момент времени (t+T), то есть через время, равное периоду колебаний.

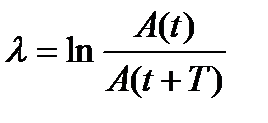
Логарифмический декремент затухания λсвязан с коэффициентом затухания β и характеризует скорость затухания амплитуды колебаний

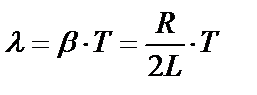
Вообще основными характеристиками затухающих колебанийявляются:

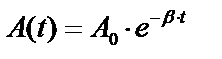- амплитуда колебаний(в момент времени t=0 она имеет максимальное значение А₀).

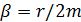- коэффициент затухания

(r - коэффициент сопротивления; m - масса)

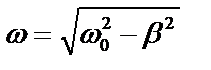- циклическая частота затухающих колебаний.

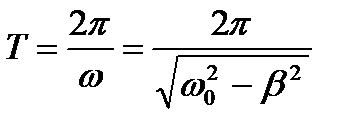- период колебаний.

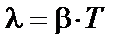- логарифмический декремент затухания.

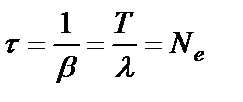- время релаксации (характеризует время, за которое амплитуда уменьшается в е раз).

Ν_е - число полных колебаний за время релаксации.

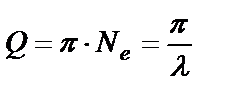- добротность контура(характеризует число колебаний за время релаксации).

Вынужденные колебания

Вынужденные колебания – это колебания, возникающие под воздействием внешней периодически меняющейся силы.

F = F₀ · cos ωt

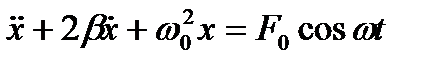-дифференциальное уравнение вынужденных

колебаний

Решением дифференциального уравнения является уравнение:

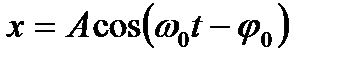
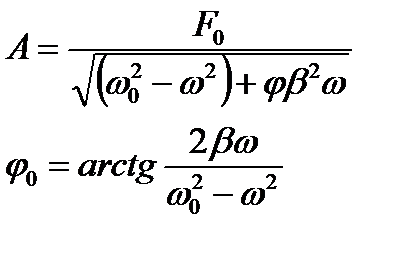
- амплитуда вынужденных колебаний

- начальная фаза

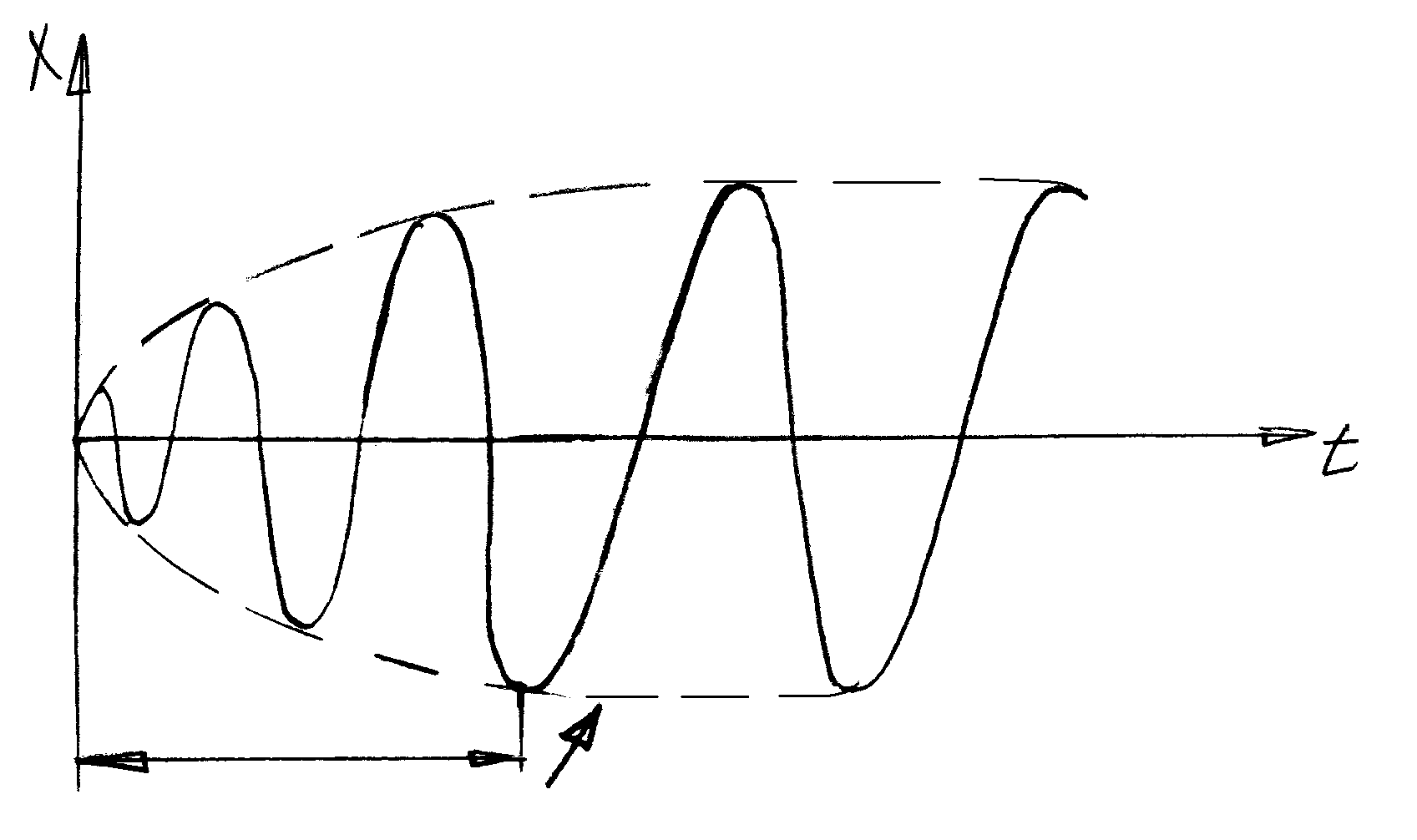
установление колебаний с частотой

При приближении частоты вынуждающей силы ( ) к собственной частоте колебательной системы ( ), наступает резкое увеличение амплитуды t - явление РЕЗОНАНСА.

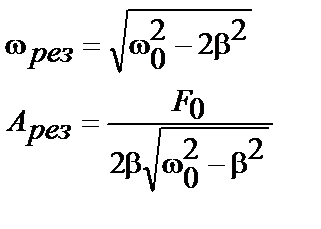
(на рис. коэффициент затухания β обозначен как δ )

ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ