Основные положения теплового расчета

Теплообменным аппаратом называется всякое устройство, назначением которого является передача тепла от, одного теплоносителя к другому. Такие аппараты многочисленны и по своему назначению и конструктивному оформлению весьма разнообразны. По принципу действия теплообменные аппараты могут быть разделены на рекуперативные, регенеративные и смесительные.

Рекуперативными называются такие аппараты, в которых горячая и холодная жидкости протекают одновременно, и тепло передается через разделяющую их стенку. Примером таких аппаратов являются паровые котлы, бойлеры, подогреватели, конденсаторы и др.

Регенеративными называются такие аппараты, в которых одна и та же поверхность нагрева омывается то горячей, то холодной жидкостью. При протекании горячей жидкости тепло воспринимается стенками аппарата и в них аккумулируется, при протекании же холодной жидкости это аккумулированное тепло передается холодной жидкости. Примером таких аппаратов являются регенераторы мартеновских и стеклоплавильных печей, воздухоподогреватели доменных печей, воздухоподогреватели Юнгстрема и др.

В рекуперативных и регенеративных аппаратах процесс передачи тепла неизбежно связан с поверхностью твердого тела. Поэтому такие аппараты называются также поверхностными.

В смесительных аппаратах процесс теплопередачи происходит путем непосредственного соприкосновения и смешения горячей и холодной жидкостей. В этом случае теплопередача протекает одновременно с материальным обменом. Примером таких теплообменников являются башенные охладители (градирни), скрубберы и др.

Специальные названия теплообменных аппаратов обычно определяются их назначением, например, паровые котлы, печи, водоподогреватели, испарители, перегреватели, конденсаторы, деаэраторы и т. д.

Несмотря на большое разнообразие теплообменных аппаратов по виду, устройству, принципу действия и рабочим телам, назначение их в конце концов одно и то же, это - передача тепла от одной, горячей жидкости к другой, холодной. Поэтому и основные положения теплового расчета для них остаются общими.

При проектировании новых аппаратов целью расчета является определение поверхности нагрева. Если же последняя известна, то целью расчета является установление режима работы аппарата и определение конечной температуры рабочих жидкостей. В обоих случаях основными расчетными уравнениями являются:

уравнение теплопередачи

Q = kF (t₁ —t₂) ккал/час (2.1)

и уравнение теплового баланса

Q = w₁f₁c_p1(t₁’ – t₁') = w₂f₂c_p2(t₂” – t₂”) ккал/час (2.2)

В этом уравнении w - часовая скорость жидкости, м/час.

Здесь и ниже индекс (1) означает, что величины относятся к горячей жидкости, а индекс (2) - к холодной. Вторым индексом (') обозначается температура при входе, а индексом (“) - при выходе рабочей жидкости из аппарата.

При выводе расчетных формул теплопередачи было принято, что в любой точке теплообменного устройства температура рабочей жидкости остается постоянной. Однако, это положение справедливо лишь при кипении жидкости и конденсации паров. В общем же случае температура рабочих жидкостей в теплообменниках изменяется - горячая охлаждается, а холодная нагревается. Вместе с этим изменяется и температурный напор между ними Δt_i = (t₁ - t₂)_i. В таких условиях уравнение теплопередачи (2.1) применимо лишь в дифференциальной форме к элементу поверхности dF, а именно:

dQ = k Δt_idF_i ккал /час.

Общее же количество тепла, переданное через всю поверхность F, определяется интегралом этого выражения:

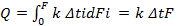ккал /час. (2.3)

Это и есть расчетное уравнение теплопередачи. Здесь Δt среднее значение температурного напора по всей поверхности нагрева. ,

В тепловых расчетах очень важное значение имеет понятие о так называемом водяном эквиваленте теплоносителя W, численная величина которого определяет собой количество воды, которое по теплоемкости эквивалентно теплоемкости часового количества рассматриваемой жидкости, т. е.

W = wγ/c_p = Vγc_p = Gc_p ккал/час °С, (2.4)

где w - часовая скорость;

V - объем часового расхода жидкости;

G - вес часового расхода жидкости.

Если ввести водяной эквивалент в уравнение теплового баланса (2.2), то оно принимает вид:

W₁ (t₁’ - t₁") = W₂ (t₂"—t₂’) ккал\час,

откуда

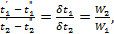(2.5)

Последнее означает, что отношение изменения температуры рабочих жидкостей обратно пропорционально отношению их водяных эквивалентов. Такое соотношение справедливо как для всей поверхности нагрева F, так и для каждого ее элемента dF, т. е.

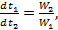(2.6)

где dt₁ и dt₂ — изменения температур рабочих жидкостей на элементе поверхности.

Характер изменения температуры рабочих жидкостей вдоль поверхности зависит от схемы их движения и соотношения значений их водяных эквивалентов. Если в теплообменном аппарате горячая и холодная жидкости протекают параллельно и в одном направлении, то такая схема движения называется прямотоком (рис. 2.1, а). Если жидкости протекают параллельно, но в прямо противоположном направлении - противотоком (рис. 2.1,б). Наконец, если жидкости протекают в перекрестном направлении - перекрестным током (рис. 2.1, в). Помимо таких простых схем движения на практике осуществляются и сложные: одновременно прямоток и противоток (рис. 2.1, г), многократно - перекрестный ток (рис. 2.1 д, в, ж) и т. д.

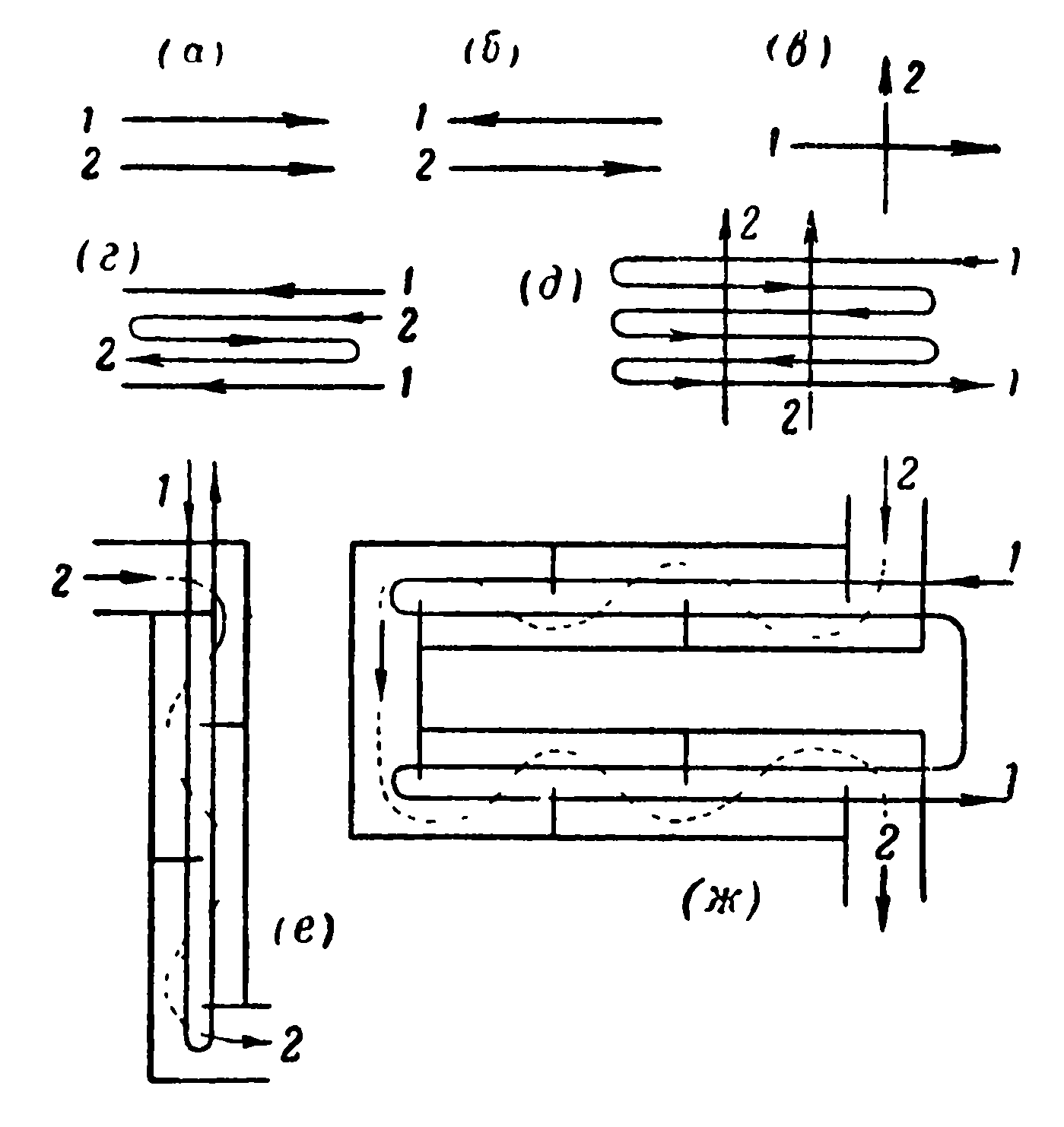
Рис. 2.1. Схемы движения рабочих жидкостей в теплообменниках.

В зависимости от того, осуществляется ли прямоток или противоток и больше W₁ или меньше, чем W₂, получаются четыре пары кривых изменения температуры вдоль поверхности нагрева, представленные на рис. 2.2. Здесь по осям абсцисс отложена поверхность нагрева F, а по осям ординат температуры рабочих жидкостей. В соответствии с уравнением (2.5) на графиках большее изменение температуры t’ - t" = δt получается для той жидкости, у которой водяной эквивалент меньше.

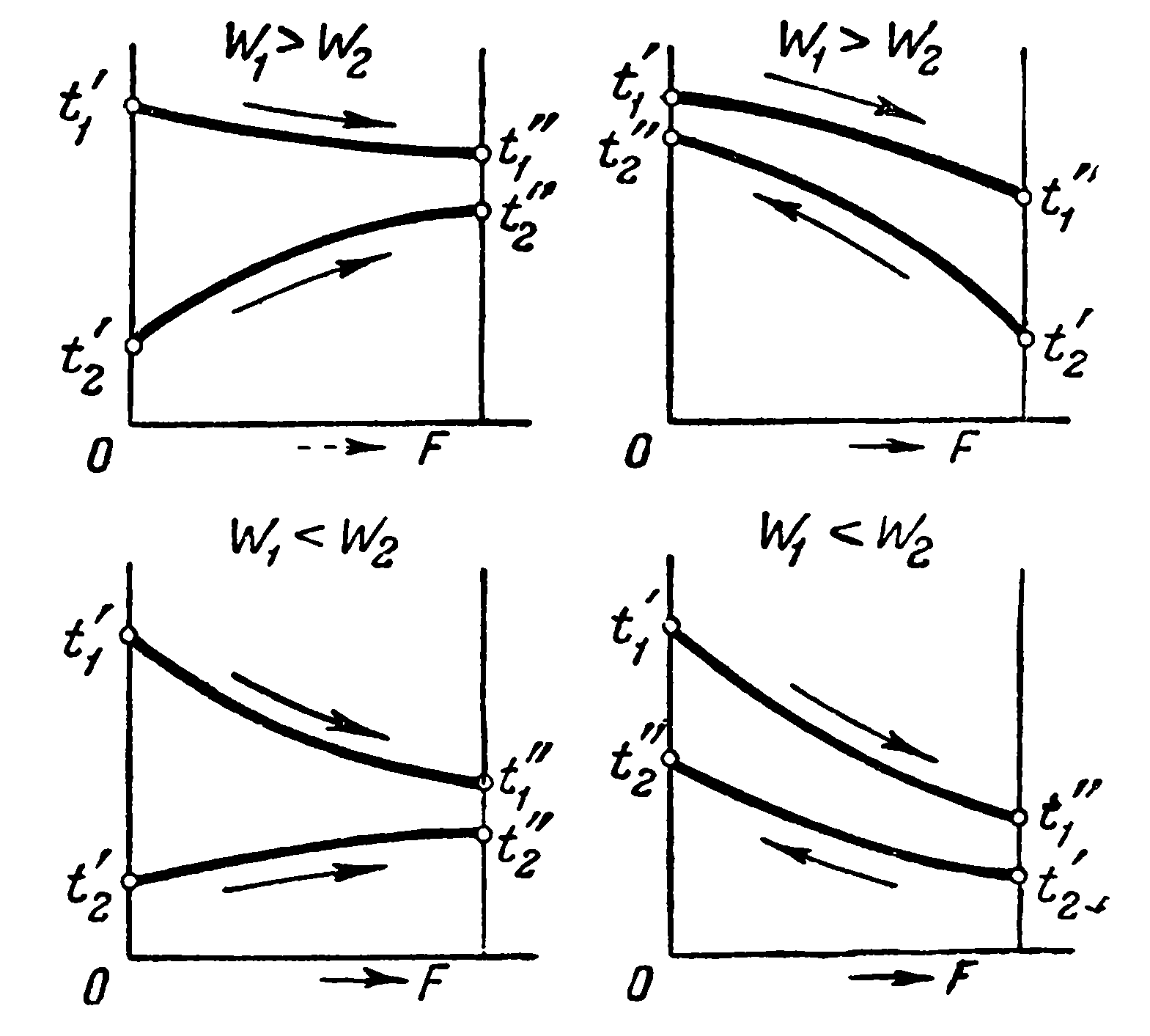
Рис. 2.2. Характер изменения температур рабочих жидкостей при прямотоке и противотоке.

Из рассмотрения графиков следует также, что при прямотоке конечная температура холодной жидкости t₂^” всегда ниже конечной температуры горячей жидкости t₁^”. При противотоке же конечная температура холодной жидкости может быть выше конечной температуры горячей. Следовательно, при одной и той же начальной температуре холодной жидкости при противотоке ее можно нагреть до более высокой температуры, чем при прямотоке; иначе говоря, при противотоке от горячей жидкости можно отвести то же количество тепла меньшим количеством охлаждающей жидкости.

Температурный напор вдоль поверхности нагрева при прямотоке изменяется сильнее, чем при противотоке. Вместе с тем среднее значение температурного напора при противотоке больше, чем при прямотоке. За счет этого при противотоке теплообменник получается компактнее. Однако, если температура хотя бы одной из рабочих жидкостей постоянна, то среднее значение температурного напора независимо от схемы движения оказывается одним и тем же. Так именно получается при кипении жидкостей и при конденсации паров, либо когда расход одной рабочей жидкости настолько велик, что ее температура изменяется ^очень мало.

Рассмотрев общие уравнения теплового расчета аппаратов и уяснив температурные условия работы теплообменников, перейдем теперь к более подробному рассмотрению величин, входящих в уравнение (2.3).

Средний температурный напор

При выводе формулы усреднения температурного напора рассмотрим простейший теплообменный аппарат, работающий по схеме прямотока. Количество тепла, передаваемого в час от горячей жидкости к холодной через элемент поверхности dF (рис, 2.3), определяется следующим уравнением:

dQ = k(t₁ – t₂)_xdF ккал час. (а)

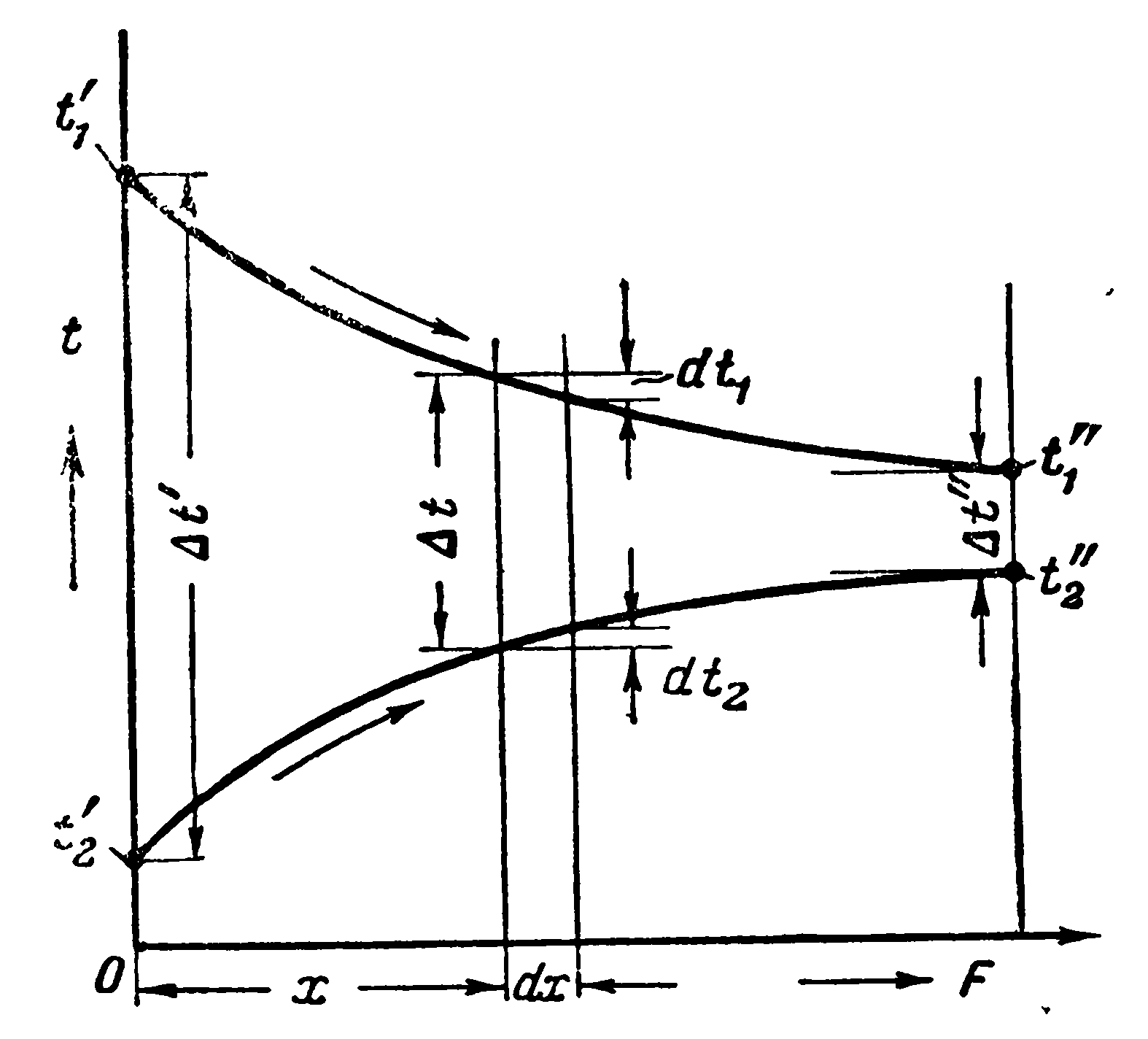
Рис. 2.3. К выводу формулы усреднения

При этом температура горячей жидкости понизится на dt1, а холодной повысится на dt₂. Следовательно,

dQ = -G₁c_p1dt₁ = G₂c_p2dt₂, (b)

откуда

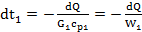(c)

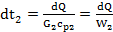(d)

Изменение же температурного напора при этом равно:

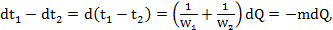(e)

где

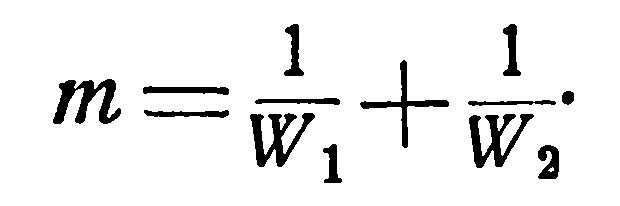
Подставляя в уравнение (е) значение dQ из уравнения (а), получим:

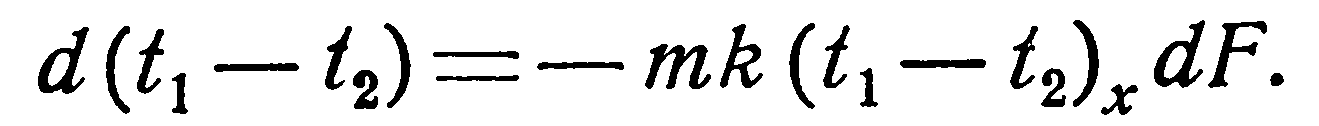(f)

Обозначим (t₁ — t₂)_x через _Δtx и произведем разделение переменных:

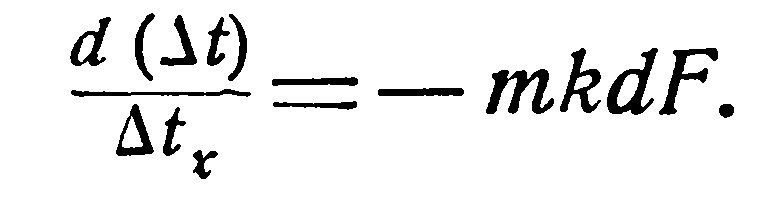(g)

Если значения m и k постоянны, то, интегрируя уравнение (g), получим:

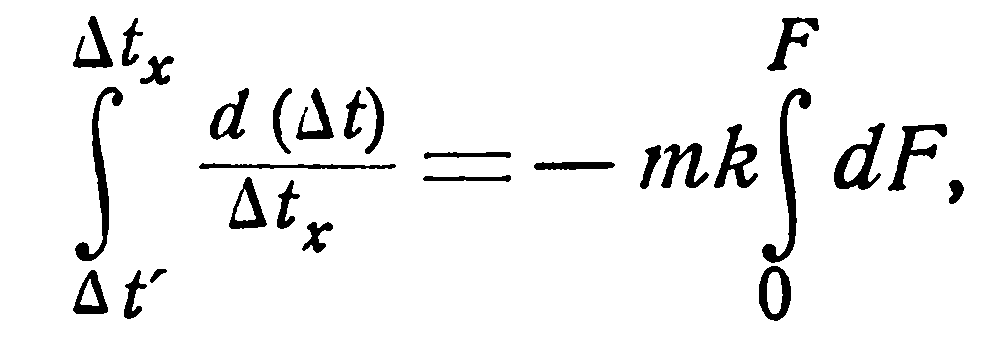
или

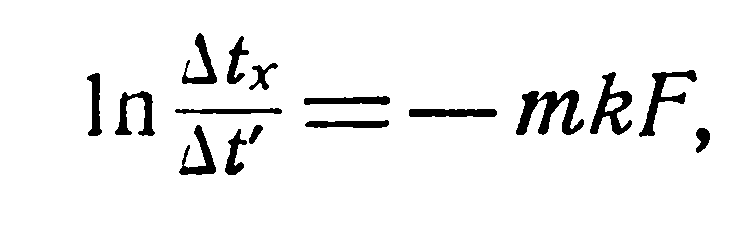(h)

откуда

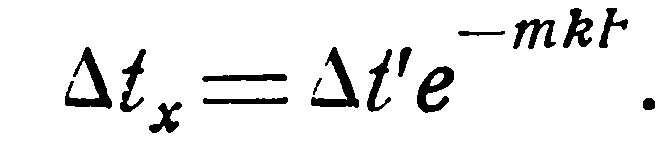(i)

Из уравнения (i) видно, что вдоль поверхности нагрева температурный напор изменяется по экспоненциальному закону. Зная этот закон, легко установить и среднее значение температурного напора Δt. На основании теоремы о среднем (при k = const) имеем:

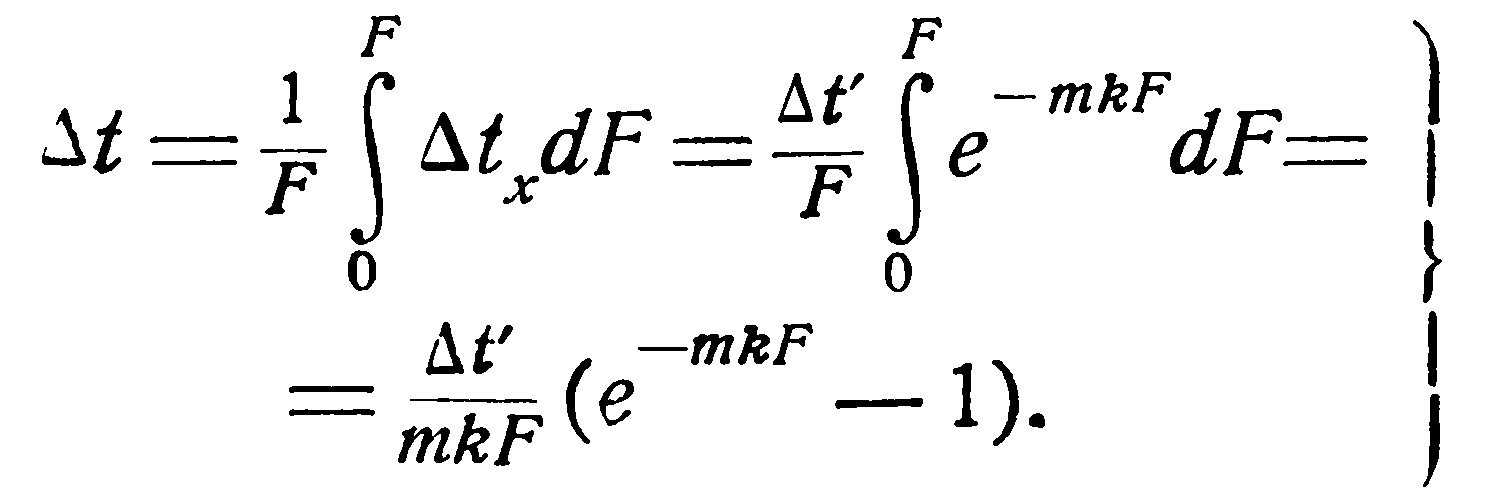(j)

Подставляя в уравнение (j) значения mkF и е^-mkF из уравнений (h) и (i) и имея в виду, что согласно рис. 2.3 в конце поверхности нагрева Δt_x = Δt", окончательно имеем:

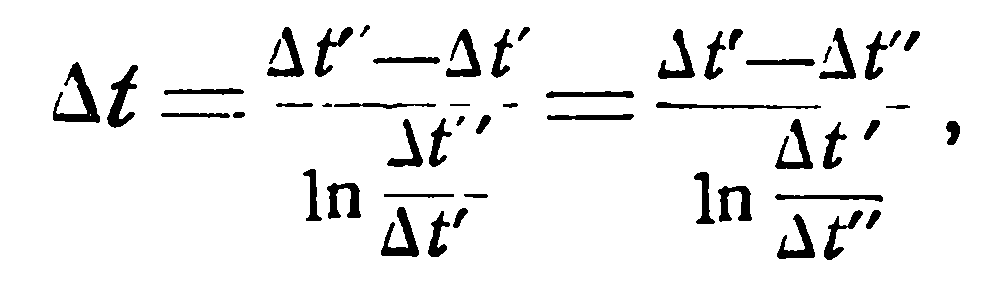(2.7)

или

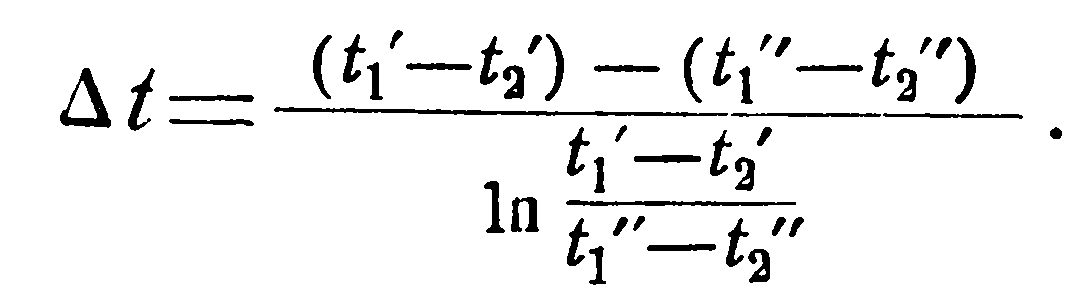(2.7’)

Такое значение температурного напора называется среднелогарифмическим.

Точно таким же образом выводится формула усреднения температурного напора и для противотока. Отличие лишь в том, чго в правой части уравнения {d) следует поставить знак минус и поэтому здесь 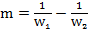. Окончательная формула для среднего температурного напора при противотоке имеет следующий вид

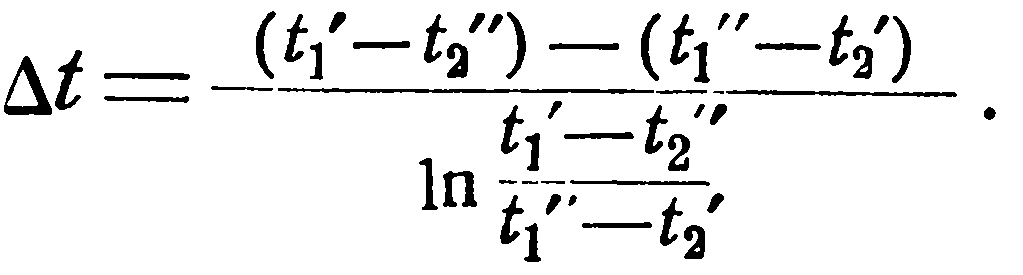(2.8)

При равенстве водяных эквивалентов в случае противотока m = 0, тогда из уравнения (i) имеем, что Δt_х = Δt’. В этом случае температурный напор по всей поверхности постоянен:

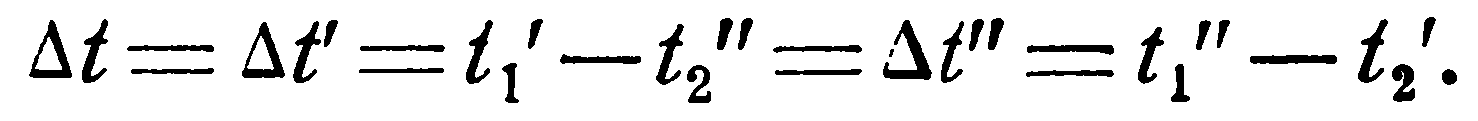(k)

Обе формулы (7) и (8) можно свести в одну, если

независимо от начала и конца поверхности через Δt’ обозначить больший, а через Δt” меньший температурные напоры между рабочими жидкостями. Тогда окончательная формула для прямотока и противотока принимает следующий вид:

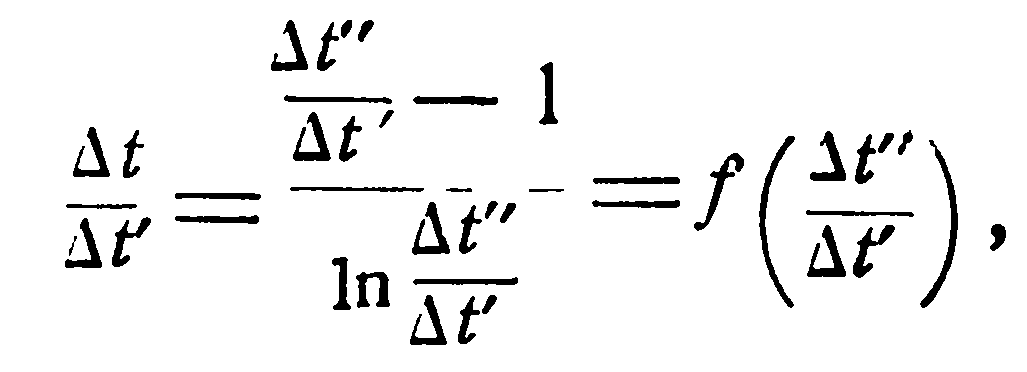(2.9)

Формула (9) представлена на фиг. 2.4; здесь по оси абсцисс нанесено значение 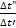, а по оси ординат значение 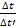,. Зная 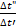и Δt’ сначала определяется 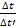, а затем и Δt .

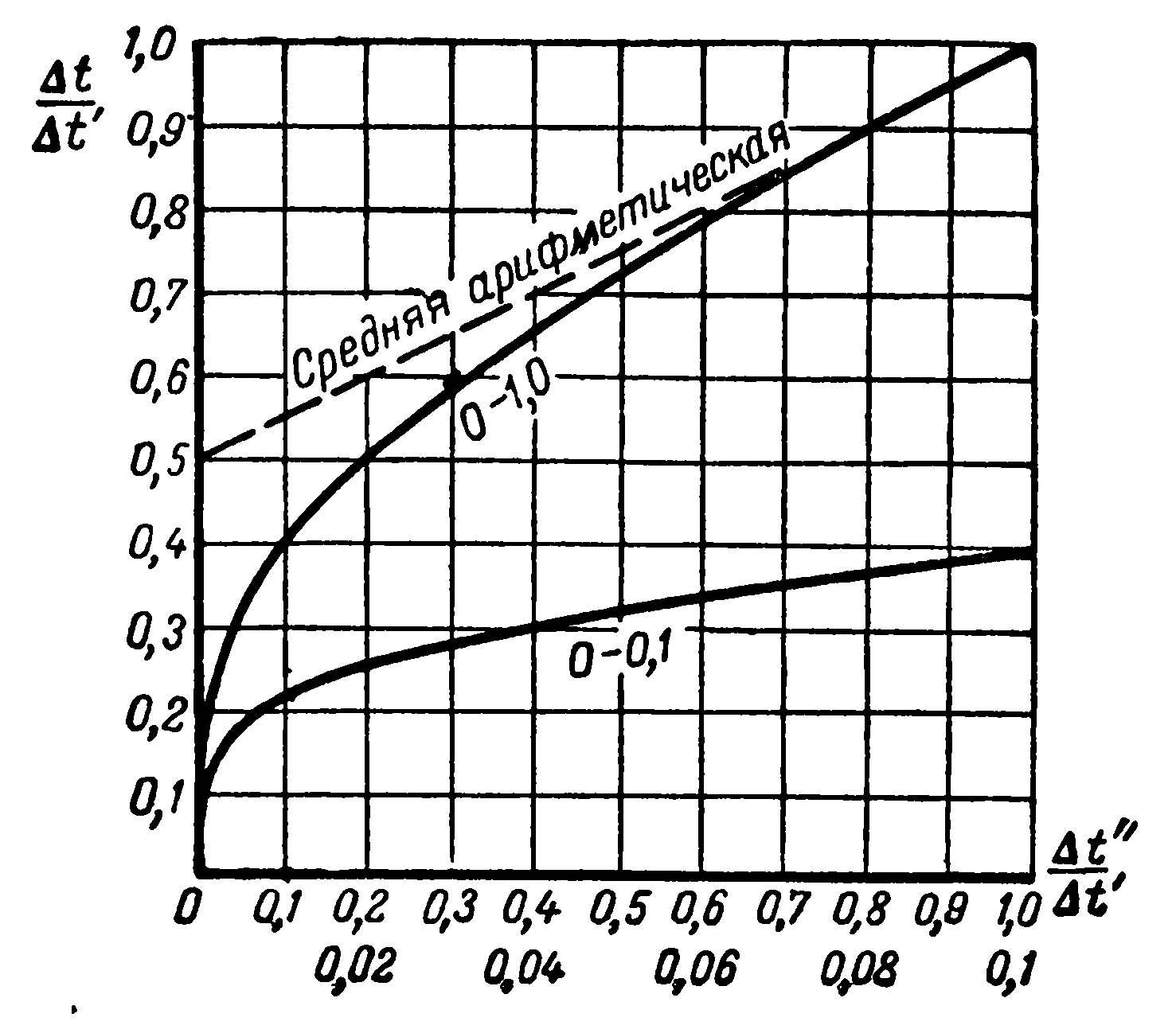
Рис. 2.4. График для определения среднелогарифмического температурного напора.

Вывод формул для среднелогарифмического температурного напора сделан в предположении, что расход и теплоемкость рабочих жидкостей, а также коэффициент теплопередачи вдоль поверхности нагрева остаются постоянными. Так как в действительности эти условия выполняются лишь приближенно, то и вычисленное по формулам (7), (8) или (9) значение Δt также приближенно. В этом слабое место расчета.

В тех случаях, когда температура рабочих жидкостей вдоль поверхности нагрева изменяется незначительно, средний температурный напор можно вычислять как среднее арифметическое из крайних напоров Δt’ и Δt"

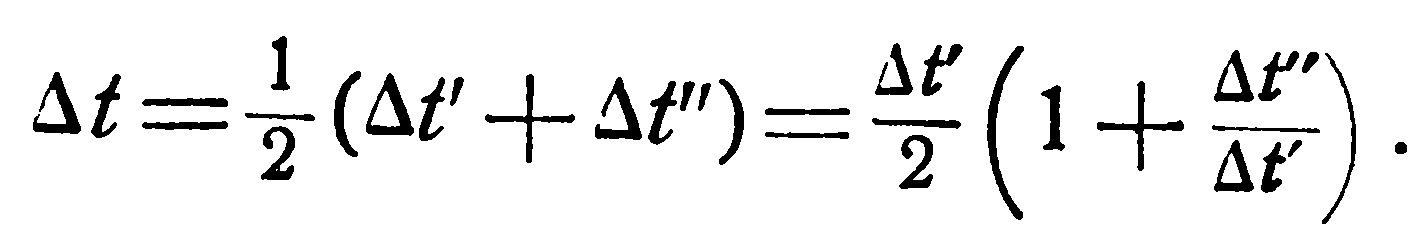(2.10)

Значение среднеарифметического всегда больше среднелогарифмического. Но при 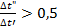они отличаются друг от друга меньше чем на 4% (рис. 2.4). Такая погрешность в технических расчетах вполне допустима.

Для аппаратов с перекрестным и смешанным током рабочих жидкостей задача об усреднении температурного напора отличается сложностью математических выкладок. Поэтому для наиболее часто встречающихся случаев результаты решения обычно представляются в виде графиков.

Пример 2.1. В холодильной установке каждый час надо охлаждать 250 л горячей жидкости с плотностью ρ₁=1100 кг/м³ и теплоемкостью с_р1 = 0,727 ккал/кг°С с t₁’ = 120 °С до t₁” = 50 °С. Для охлаждения располагаем 1000 л воды в час при t₂’ = 10 °С. Определить потребную поверхность нагрева при прямотоке и противотоке, если k =1 000 ккал/м³час°С.

Сначала определим водяные эквиваленты W₁ и W₂:

W₁ = 0,250 1100·0,727 = 200 ккал/час°С,

W₂ = 1 1000 1 = 1 000 ккал/час °С.

Подставляя их значения в уравнение (5), получим конечную температуру воды t₂”

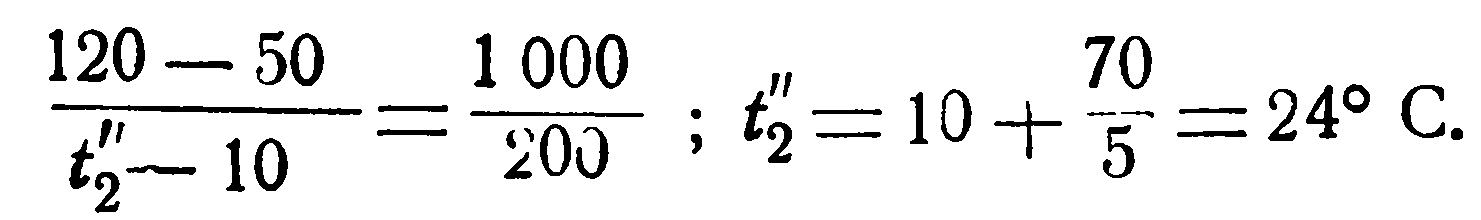
Теперь определим среднюю разность температур.

При прямотоке:

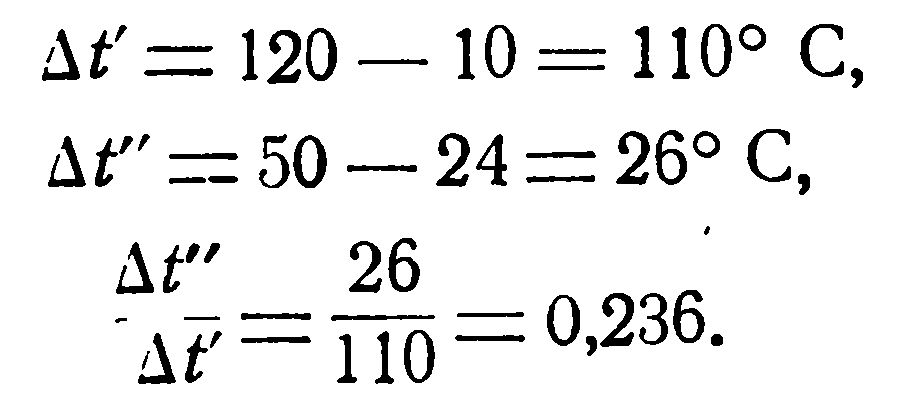
По графику (рис. 2.4) находим:

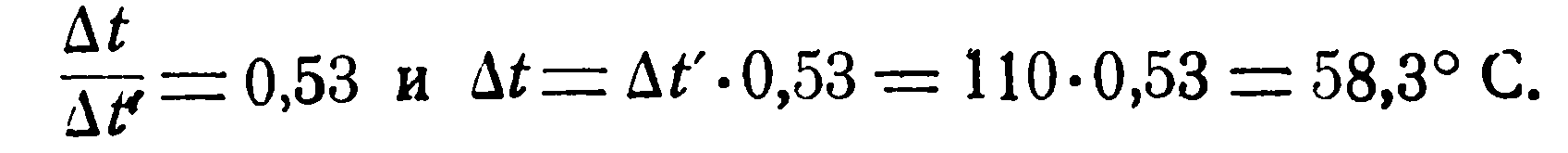
При противотоке:

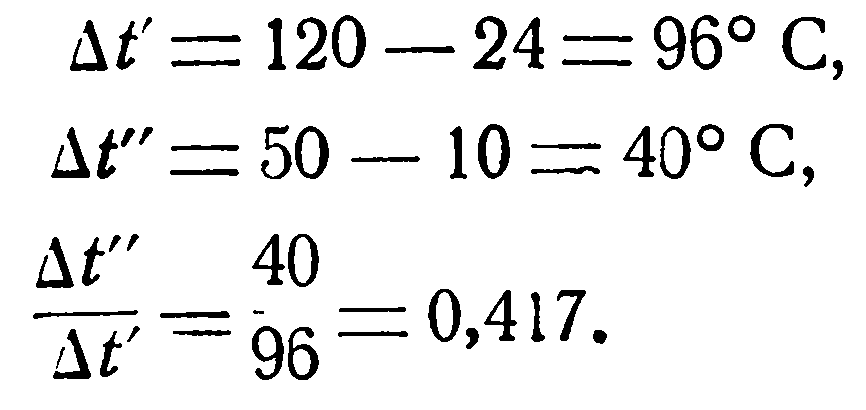
По графику (фиг. 2.4) находим 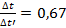и Δt=Δt’·0,67=96·0,67=64,3°С.

Количество переданного тепла определяется по уравнению (2):

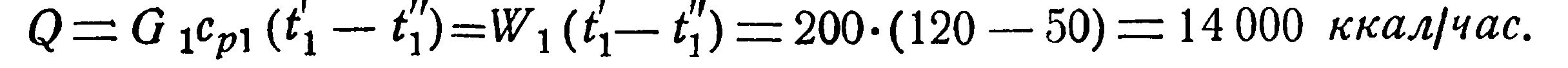
Имея значения Q и Δt, по уравнению (1) легко определить произведение kF,

При прямотоке:

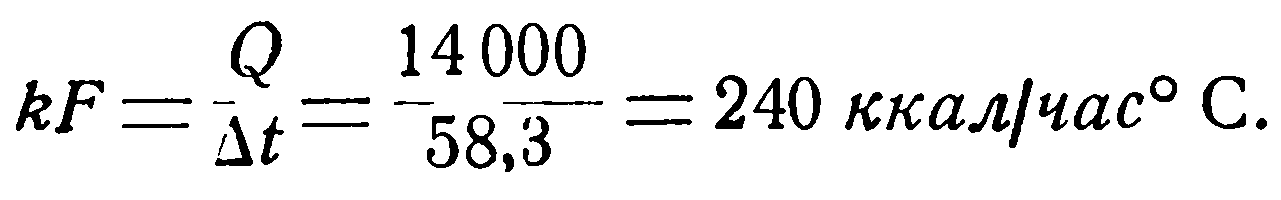
При противотоке:

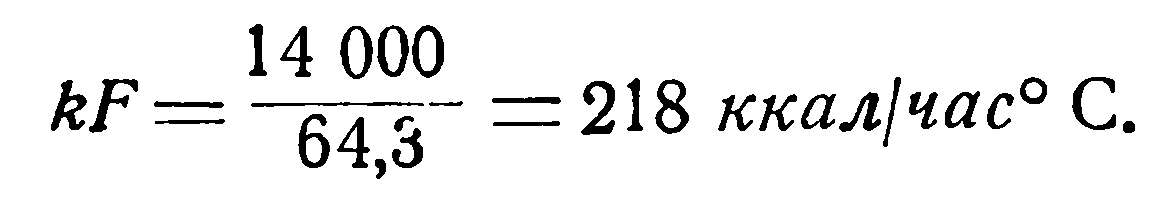
Следовательно, при прямотоке 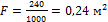и при противотоке .

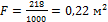Теплопередача в аппаратах

При расчете теплообменных аппаратов большие трудности возникают при выборе значения коэффициента теплопередачи k. Эти трудности в основном определяются изменением температуры рабочих жидкостей и сложностью геометрической конфигурации поверхности теплообмена. Влияние этих факторов трудно учесть. Специфические же особенности процесса теплообмена в рассчитываемых аппаратах учитываются при выборе значений коэффициентов теплоотдачи а.

При расчете коэффициента теплопередачи в первую очередь необходимо произвести анализ частных термических сопротивлений, и если возможно, то следует произвести упрощение расчетной формулы.

Далее необходимо учесть влияние на коэффициент теплопередачи изменения температуры рабочих жидкостей. Большей частью такой учет сводится к отнесению коэффициентов теплопередачи к средним температурам рабочих жидкостей. Для жидкости с большим водяным эквивалентом средняя температура берется как среднеарифметическое из крайних значений, например, t_б = 0,5 (t_б’ + t_б”). При этом для другой жидкости, с меньшим водяным эквивалентом, средняя температура определяется из соотношения: t_m = t_б ± Δt. Здесь Δt является среднелогарифмическим температурным напором; знак минус (-) применяется в тех случаях, когда t_б означает температуру горячей жидкости, а знак плюс (+) в тех, когда t_б означает температуру холодной.

Иногда вычисление коэффициента теплопередачи производят по температурам рабочих жидкостей в начале и в конце поверхности нагрева. Если полученные значения k’ и k" друг от друга отличаются не очень сильно, то среднеарифметическое из них принимается за среднее значение коэффициента теплопередачи k, а именно:

k=0,5 (k' + k"). (2.11)

В большинстве практических случаев такое усреднение является достаточным. В случае же сильного расхождения между собой значений k’ и k" необходимо разделить поверхность нагрева на отдельные участки, в пределах которых коэффициент теплопередачи изменяется незначительно, и для каждого такого участка расчет теплопередачи производить раздельно.

Так же поступают и в тех случаях, когда резко меняются условия омывания поверхности нагрева рабочей жидкости, например, в нижней части поверхности нагрева поперечное омывание, в средней продольное и в верхней - снова поперечное. Если при этом температура рабочей жидкости изменяется незначительно, то применяется следующее усреднение:

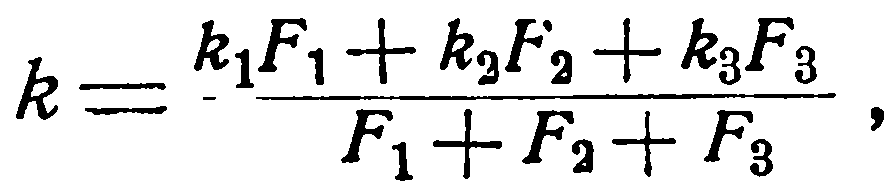(2.12)

где F₁, F₂ и F₃ - отдельные участки поверхности нагрева;

k₁, k₂ и k₃ - средние значения коэффициента теплопередачи на этих участках.