Методы информационного параметра

Методы связаны с прохождением через радиоустройства информационного параметра .

Входными сигналами моделей могут являться: информационный параметр , полезное сообщение или его параметры, а также помехи или их параметры.

Выходными сигналами являются либо оценка информационного параметра), либо связанный с ней выходной сигнал устройства .

Формульный метод

Используется, когда оказывается возможным описание преобразований информационного параметра в выходной сигнал , при котором гарантируется статистическая эквивалентность модели и радиоустройства.:

(!)

- некоторые функционалы.

Методы статистических эквивалентов

Метод применим, когда удается найти статистическое описание или на выходе с достаточной для моделирования точностью.

Описание сигнала на выходе дискриминатора на основе метода статистических эквивалентов

Дискриминатор – это нелинейное звено следящей системы, вырабатывающее сигнал, зависящий от ошибки слежения.

Напряжение на выходе дискриминатора:

- математическое ожидание напряжения (неслучайная составляющая)

- шумовое напряжение (случайная составляющая).

Усреднение производится за время, много большее периода несущей частоты сигнала и много меньше, чем , - максимальная частота в спектре информационного параметра.

В этом случае не успевает существенно измениться и тогда

- дискриминационная характеристика дискриминатора. В отсутствии помех совпадает с детекторной характеристикой.

В общем случае форма дискриминационной характеристики зависит от отношения сигнал/шум на входе дискриминатор.

Полагаем, что на входе дискриминатора действует помеха, имеющая нормальное распределение.

Для описания шумового напряжения на выходе дискриминатора используется корреляционная функция:

.

Спектральная плотность мощности

Параметр можно исключить из записи, т.к. меняется медленно.

Из графика видно, что спектральная плотность мощности шума достаточно равномерна в пределах полосы пропускания, значит шум на выходе дискриминатора можно моделировать как белый шум.

На выходе дискриминатора всегда есть цепи, которые выделяют из шумов узкую полосу частот:

.

- флюктуационная характеристика дискриминатора.

Если изменения не приводят к изменению спектрального состава шумового напряжения на выходе дискриминатора, а вызывают лишь изменение его интенсивности, и спектральная плотность мощности постоянна, то

- нормированный белый шум с единичной спектральной плотностью.

, определяются в результате анализа реального дискриминатора.

Статистический эквивалент имеет вид:

При цифровом моделировании .

Модель фазового детектора по методу статистических эквивалентов

На входе ФД действует смесь сигнала с узкополосной помехой:

Опорное напряжение

Фазы сигнала, помехи и опорного колебания - это медленно меняющиеся функции времени.

Структурная схема ФД:

Информационным параметром является фаза

Первое слагаемое – дискриминационная (детекторная) характеристика и оно не зависит от отношения с/ш на входе ФД.

Второе слагаемое связано с взаимодействием помехи и опорного колебания и не зависит от информационного параметра .

При усреднении второе слагаемое обращается в 0.

Информационный параметр является медленно меняющейся функцией времени.

Спектральная плотность мощности шума на выходе ФД:

.

Значение спектральной плотности мощности выходного напряжения определяется биениями опорного колебания амплитудой и частотой с составляющими спектра помехи сосредоточенными в окрестности частот .

Спектр мощности биений получается смещением спектров помехи в области низких частот и последующим суммированием результатов.

Спектральная плотность мощности помехи на выходе в результате биений опорного колебания на каждой из частот с соответствующими составляющими помехи есть:

Результирующая спектральная плотность

В предположении равномерной спектральной плотности, достаточно взять соотношение

Модель замкнутой следящей системы по методу информационного параметра

Рассмотрим на примере ФАПЧ

Фазовый детектор сравнивает полную фазу напряжения гетеродина с полной фазой напряжения входного сигнала

.

Фаза напряжения входного сигнала отсчитывается относительно фазы напряжения гетеродина.

- частота свободных колебаний гетеродина;

- начальная фаза колебаний гетеродина.

При петлевом управляющем напряжении в петле ФАПЧ начальная частота гетеродина образует с частотой сигнала начальную разность частот , которая устраняется в процессе захвата. Фаза учитывает относительную начальную разность фаз напряжений сигнала и гетеродина. Напряжение с выхода ФД фильтруется, усиливается и управляет частотой гетеродина так, чтобы уменьшилась разность частот гетеродина и сигнала . Если частота входного сигнала близка к частоте колебаний гетеродина и постоянна, то действие ФАПЧ приведет к тому, что частота гетеродина оказывается «захваченной» входным сигналом, а разность фаз между напряжениями сигнала и гетеродина имеет конечную величину. Эта разность фаз необходима для выработки напряжения рассогласования , с помощью которого происходит перестройка гетеродина от частоты свободных колебаний в разомкнутой системе на частоту сигнала. ФНЧ ослабляет высокочастотные составляющие напряжения, управляющего частотой гетеродина, и корректирует передаточную функцию замкнутой системы.

Аналоговая модель ФАПЧ

Напряжение на выходе ФНЧ:

Напряжение на выходе усилителя:

- коэффициент усиления усилителя

Частота гетеродина:

- чувствительность управителя.

Фаза гетеродина:

На модели могут быть исследованы следующие характеристики системы:

1) переходные процессы при захвате частоты;

2) полоса захвата;

3) срывы слежения за частотой сигнала.

Цифровая модель ФАПЧ

Задержка 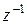ставится для упрощения вычислений, в каждом такте моделирования не приходится решать нелинейное относительно уравнение. Нелинейность содержится в .

В качестве ФНЧ может быть использовано инерционное звено:

Очень часто для обеспечения устойчивости используется пропорционально-интегрирующий фильтр, у которого при :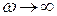

.

Используем метод билинейного Z-преобразования для обеспечения наилучшего совпадения частотных характеристик аналоговой и цифровой моделей.

.

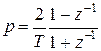Так как блоки соединены последовательно, то можно объединить в один блок.