Цифровое моделирование нелинейных узлов р/устройств

Нелинейные узлы делятся на 4 части:

1) Безынерционные нелинейные звенья (БНЗ).

Цифровое моделирование таких узлов связано с преобразованием входного сигнала в выходной в соответствии с характеристикой нелинейности:

.

Если задана аналитически, моделирование осуществляется путем вычисления по формуле; если задана графически или таблицей, то моделирование осуществляется с помощью таблиц.

2) Нелинейные инерционные функциональные разомкнутые звенья.

Это звенья, в которых можно выделить развязанные относительно друг друга линейные инерционные и безынерционные звенья.

- передаточные функции линейных инерционных звеньев.

3) Нелинейные инерционные функциональные замкнутые звенья.

К таким замкнутым звеньям сводятся большинство следящих устройств.

4) Нелинейные инерционные нефункциональные звенья.

Способ моделирования – с помощью нелинейных ДУ.

Рассмотрим моделирование нелинейных инерционных функциональных замкнутых звеньев.

Пусть звено с 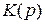- это фильтр первого порядка с постоянными коэффициентами

Пусть .

Тогда:

В каждом такте моделирования надо решать нелинейное относительно уравнение. Это всегда имеет место при моделировании замкнутых функциональных нелинейных узлов.

Для упрощения вычислений используют вычисленные в предыдущем такте значения Y. Получим:

В модель вводится блок 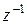. Введение этого блока приводит к дополнительной ошибке, которую можно сделать сколь угодно малой, уменьшая Т. Получаем:

Одно и то же устройство может принадлежать к любому из 4-ех классов.

Рассмотрим амплитудный детектор.

1. Как устройство первого класса АД моделируется, если моделируются его функциональные преобразования (формально описывается преобразование сигнала).

.

Недостаток данной цифровой модели: необходимость помнить всю реализацию входного сигнала от до .

2. Если надо проанализировать возможные искажения огибающей сигнала, вызванные, допустим, неправильным выбором постоянной времени фильтра, то детектор моделируется как устройство 2-ого класса. В этом случае добавляется фильтр с передаточной функцией 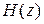и этот фильтр – цифровая модель RC-цепи.

3. Если при моделировании надо учесть реакцию нагрузки на диод, то детектор моделируется как устройство 3-его класса.

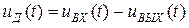
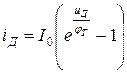
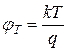- температурный потенциал

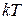- тепловая энергия

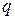- заряд

;

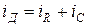
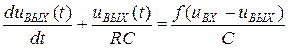
Переход от тока диода к выходному напряжению осуществляется с помощью линейного инерционного звена, имеющего передаточную функцию, определяемую нагрузкой детектора:

.

.

4. Если требуется учесть инерционные свойства диода, то АД моделируется как 4-ый класс. Решение – решение нелинейного дифференциального уравнения.

Моделирование основных нелинейных р/технических преобразований

К таким преобразованиям относятся:

1) модуляция;

2) преобразование частоты;

3) детектирование АМ-, ЧМ-, ФМ-сигналов.

Модуляция

1) Всякая функция времени может быть получена в результате решения на ЭВМ дифференциального уравнения.

2) Можно моделировать с помощью рекурсивных фильтров (полагая, что фильтры соответствуют колебательным цепям большой добротности).

Преобразование частоты

См. моделирование р/приемного устройства методом комплексной огибающей на основе функциональной схемы.

Имеется сигнал:

.

Процесс преобразования частоты сводится к переносу частоты с сохранением амплитудных и фазовых соотношений.

.

.

Таким образом, с функциональной точки зрения преобразование частоты сводится к замене в математической модели сигнала частоты на .

Детектирование

Пусть задан узкополосный сигнал:

.

Процесс представляется квадратурными составляющими:

Требуется разработать алгоритмы, которые по известным квадратурным составляющим позволяют получить дискретные последовательности ; ; , соответствующим процессам амплитудного, фазового и частотного детектирования.

Для амплитудного детектора:

Для фазового детектора:

Напряжение на выходе ФД пропорционально

Для частотного детектора:

Частота – это производная от фазы

- текущее значение частоты.