Модель апериодического усилителя на основе схемы замещения.

Схема замещения

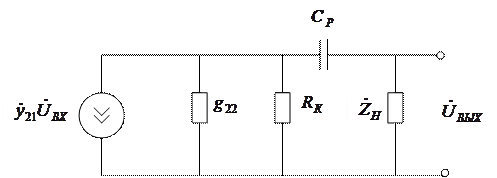Коэффициент передачи для всей области частот:

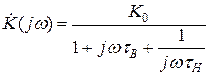
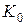( - коэффициент передачи на средней частоте)

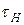- постоянная времени в области нижних частот

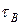- постоянная времени усилителя в области верхних частот (учитывает инерционные свойства).

Записываем коэффициент передачи в операторной форме:

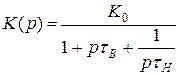
Изображение выходного напряжения:

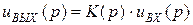
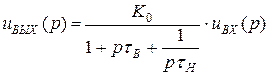
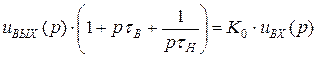
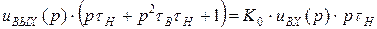
От изображения переходим к оригиналу, вспоминая, что умножение на р – операция дифференцирования.

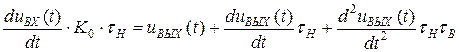
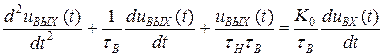
Получили линейное дифференциальное уравнение второго порядка, которое может быть решено на ЭВМ стандартными методами при задании .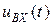

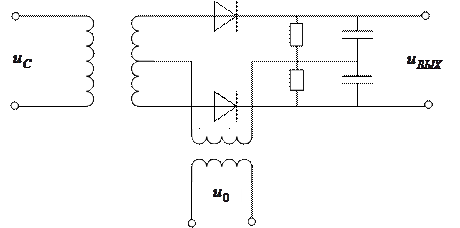
Модель фазового детектора на основе структурной схемы.

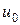- мгновенное значение опорного напряжения

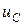- мгновенное значение сигнального напряжения.

ФД сравнивает фазу сигнального напряжения с фазой опорного напряжения.

.

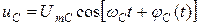
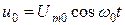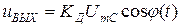
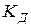- коэффициент передачи.

Перемножаем напряжения:

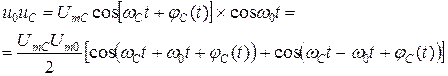
Разность частот 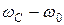практически равна 0.

На основе анализа последней формулы вытекает схема ФД.

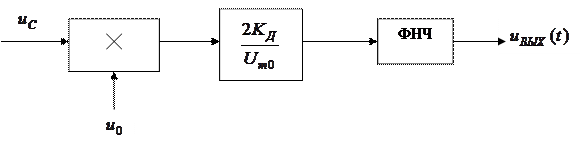ФНЧ – фильтр нижних частот (отфильтровывает частоты 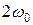и пропускает разностные частоты.

В качестве ФНЧ может быть использовано инерционное звено.

Описывается ДУ первого порядка.

Использование метода несущей для моделирования РПрУ на основе функциональной схемы.

Сигнал на входе:

.

- собственный шум, например, приведенный ко входу приемника.

- помехи.

УРЧ: 1) ДУ;

2) спектральный метод;

3) временной метод;

4) с использованием методов цифровой фильтрации.

При спектральном методе используется алгоритм: (устанавливается связь выходного сигнала с входным)

.

.

.

Временной метод:

При временном методе используются интегралы Дюамеля

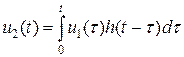
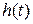- импульсная характеристика.

Дискретное представление интеграла Дюамеля

n – текущее значение момента времени.

Получили формулу для вычисления реакции нерекурсивного фильтра.

Преобразователь частоты (ПЧ).

Его можно промоделировать как перемножитель.

Для простоты опускаем начальную фазу.

.

.

Фильтр настроен на .

УПЧ: линейный избирательный усилитель. Он может быть промоделирован как и УРЧ четырьмя методами.

Детектор может быть промоделировать с помощью ДУ.

Видеоусилитель – линейная цепь.

Метод комплексной огибающей

Сущность метода сводится к замене реального р/звена моделью низкочастотного звена с входным воздействием в виде комплексной огибающей реального узкополосного сигнала. Метод применяется, как правило, при моделировании на основе принципиальных схем, структурных и функциональных схем. Метод применяется для узкополосных сигналов, у которых 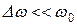( 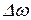- ширина спектра, 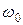- частота несущей).

Сигнал описывается следующим образом:

.

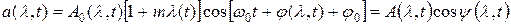В общем случае между 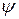и 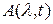нет однозначного соответствия. Неоднозначность можно избежать введением комплексного или аналитического сигнала:

,

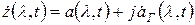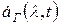- сигнал, сопряженный по Гильберту.

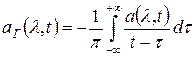
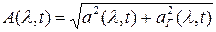(1)

.

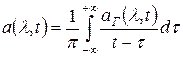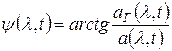(2)

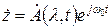
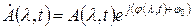
В 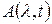заложена вся информация об АМ.

Ф-ла (1) является математической моделью идеального детектора, ф-ла (2) – мат. моделью идеального фазового детектора.

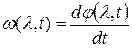(3)

Ф-ла (3) – математическая модель идеального фазового детектора.

При таком описании сигнала исключается множитель 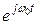, который является переносчиком информации.

Моделирование по методу комплексной огибающей сводится к разработке алгоритма, связывающего комплексные огибающие на входе и выходе.

Получаемая модель является низкочастотной, так как комплексная огибающая сигнала – это медленно меняющаяся во времени функция.

В методе экономится машинное время и память.

Моделирование процесса преобразования комплексной огибающей сигнала линейной цепью.

Сигнал на выходе связан с входным воздействием: (интеграл Дюамеля):

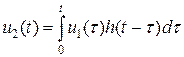(4)

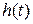- импульсная характеристика цепи.

Для низкочастотного эквивалента цепи можно записать:

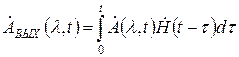(5)

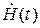- комплексная импульсная характеристика.

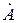- комплексная огибающая.

Комплексную огибающую на выходе линейной цепи можно промоделировать прямо по формуле (5) (в универсальной ЭВМ, где есть представление комплексных чисел).

В случае (5) по сравнению с (4) количество операций сложения и умножения будет больше. Можно разработать рекурентные соотношения, с помощью которых можно будет моделировать быстрее, но не точнее.

Если в ЭВМ нет представления комплексных чисел, то фильтр с импульсной характеристикой 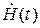можно будет промоделировать с помощью четырех фильтров, имеющих действительные импульсные характеристики.

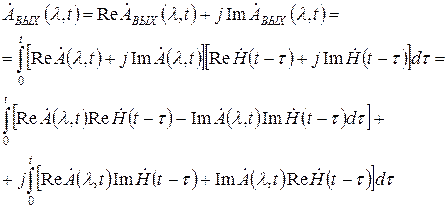
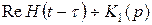
¸ - прямое преобразование Лапласа.

.
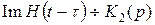