Общие сведения математической теории управления запасами
Математическое моделирование управления запасами используется для оценки оптимального запаса материальных ресурсов, предметов потребления, товаров различного вида и т.п. с целью удовлетворения спроса на некотором интервале времени. В любой задаче управления запасами требуется определять количество заказываемой продукции и сроки размещения заказа.
Многие примеры, приводимые в настоящем пособии, будут затрагивать создание запаса товаров в магазине. Однако запасы необходимы практически для любой организации. Это и запасы канцтоваров в офисе, и запасы деталей и заготовок на заводе, и запасы удобрений и ГСМ в сельскохозяйственном предприятии и т.д.
Имеющийся спрос можно удовлетворить по-разному. Существует два крайних случая:
· создать большой запас на весь предполагаемый период действия организации (на весь срок годности товара, на весь имеющийся объем склада и т.п.) и из этого запаса удовлетворять все поступающие заявки (крайне избыточный запас);
· завозить товар по мере поступления заявки (полное отсутствие запаса).
Достоинствами первого варианта является минимум затрат на оформление и доставку запасов, минимизация рисков дефицита, возможные скидки от объемов закупки. Недостатки первого варианта – большие капиталовложения в организацию хранения товара, риски порчи и устаревания товара.
Второй способ имеет высокую себестоимость организации поставок и высокие риски дефицита, однако не требует больших затрат средств на хранение.
В большинстве организационных и торговых систем организация поставок обоими крайними способами приводит к значительным затратам. Необходим некоторый промежуточный вариант, минимизирующий совокупные затраты. Заметим, что обычно объем спроса не зависит от организации поставок и определяется потребностями в товаре. В связи с этим суммарный объем поставок за интервал времени должен быть неизменным. В частности, если поставки могут осуществляться только одинаковыми партиями размера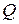 
, а число таких партий за интересующий интервал времени равно 
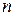, то их произведение постоянно:
.
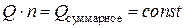Совокупные затраты системы управления запасами в самом общем случае можно выразить в виде следующей суммы:
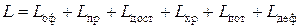
где участвуют следующие составляющие:
· 
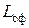– затраты на оформление заказа;
· 
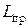– затраты на приобретение заказа;
· 
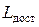– затраты на доставку заказа;
· 
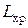– затраты на хранение заказа;
· 
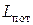– затраты на потерю заказа (потери при порче товара или снижении его продажной цены);
· 
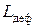– затраты на дефицит (выплаты неустоек при отсутствии товара, потеря репутации, недополучение прибыли).
Затраты на оформление заказапредставляют собой расходы, связанные с его подбором и оформлением. Они обычно слабо зависят от размера заказа и во многих моделях принимаются постоянными. В этом случае, при организации поставок мелкими партиями затраты на оформление растут пропорционально количеству этих партий, а увеличение размера партии поставки соответственно снижает их.
Затраты на приобретение определяются закупочной ценой на единицу товара. В случае неизменности цены в зависимости от объема поставки эти затраты за общую сумму заказов постоянны и не зависят от размеров партий. Ситуация заметно меняется, если используются скидки в зависимости от размера партии заказа (оптовые скидки).
Затраты на доставку заказа могут быть постоянными для каждой партии (в случае, когда вся партия доставляется единым средством и не превышает его размеры) и пропорциональными размеру партии (когда доставляется большое количество товара и средства доставки пропорциональны размерам заказа). В первом случае эти затраты аналогичны затратам на оформление и растут пропорционально количеству партий заказа. Во втором случае имеем аналог затрат на приобретение, они не меняются в зависимости от количества партий и едины для неизменной общей суммы заказа.
Затраты на хранение запаса представляют собой расходы на организацию хранения (аренда или покупка помещений, зарплата складского персонала) и содержание запасов на складах (энергозатраты на холодильные и/или нагревательные установки и т.п.). В зависимости от системы хранения эти затраты могут быть пропорциональны размеру максимального количества запаса (при организации больших складских помещений) или пропорциональны произведению текущего количества запаса на время его хранения (при малых запасах).
Затраты на потерюзаказа или его части представляют собой потерю прибыли из-за порчи товаров, их устаревания или окончания срока годности.
Затраты на дефицит складываются из сумм штрафных санкций, выплачиваемых предприятием при невозможности удовлетворения спроса, сумм недополученной прибыли из-за нехватки определенных ресурсов или падения репутации организации.
Заметим, что в некоторых случаях определенные виды затрат бывают несущественными для моделирования или просто отсутствуют. Бывают случаи, когда некоторые затраты (например дефицит или потери товара) невозможны или недопустимы по сути экономической или технологической постановки задачи.
На рисунке 1. представлена типовая схематическая зависимость затрат каждого вида и суммарных затрат от размера партии заказа. По рисунку видно, что при некотором оптимальном объеме партии заказа достигается минимум совокупных затрат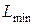 
.
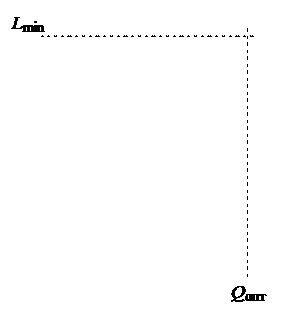
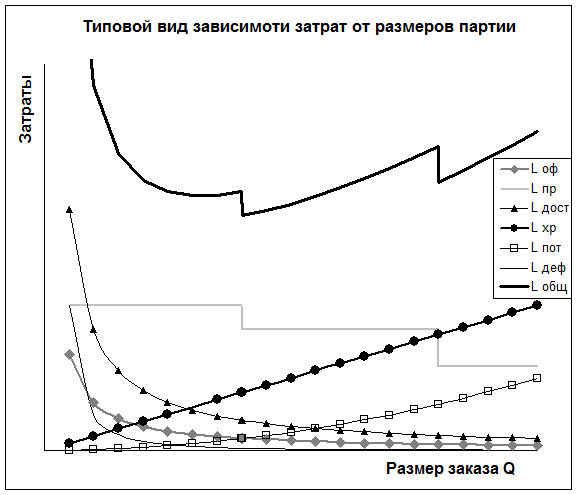
Рис. 1.
В результате анализа мы должны дать ответ на два основных вопроса:
· Сколько ресурса заказывать?
· Когда заказывать?
В качестве ответа на первый вопрос мы должны определить оптимальный размер заказа – количество ресурсов, которое необходимо поставлять каждый раз, когда происходит размещение заказа.
В качестве ответа на второй вопрос мы должны определить оптимальную точку заказа – момент, когда необходимо производить заказ. В зависимости от системы УЗ, точка заказа может определяться как временем (момент заказа), когда необходимо размещать заказ, так и количеством товара, оставшегося в системе (уровень запаса), при котором необходимо делать новую заявку.
Обычно при осуществлении периодического контроля состояния запасов (раз в день, неделю, месяц и т.д.) необходимо обеспечивать поставку нового количества ресурсов в объеме размера заказа через равные интервалы времени, совпадающие с интервалами периодического контроля. Примером такой системы может служить организация запасов канцтоваров в офисе с ежемесячным или ежеквартальным сбором отчетов об использовании и заявок.
При осуществлении непрерывного контроля состояния запаса необходимо размещать новый заказ в размере объема запаса, когда его уровень достигает точки заказа.
Модель Уилсона
Простейшей моделью управления запасами является Модель Уилсона. Эта модель достаточно хорошо описывает незначительные поставки продуктов первой необходимости (хлеб, молоко и т.п.), организацию запасов предметов обеспечения текущей деятельности организации (канцтовары, электротовары и т.п.), поставки запчастей для механизмов и расходных материалов и ряд других ситуаций.
В модели Уилсона принимаются следующие допущения.
1. Имеется внешний неограниченный источник товара. Заказ доставляется от поставщика, у которого имеется неограниченное количество товара или со склада, на котором хранится ранее произведенный товар в достаточно больших количествах.
Неограниченность товара необходимо понимать в рамках данной задачи следующим образом. Количество товара у поставщика или на складе должно быть таким, чтобы удовлетворить каждый раз любую требуемую нами заявку. Например, для розничного магазина, закупающего по 5-10 коробок товара в день, достаточно, чтобы на складе постоянно находилось не менее 10 коробок товара.
2. Известна интенсивность потребления, и она не меняется с течением времени. Это справедливо, когда отсутствуют сезонные или недельные колебания спроса или ими можно пренебречь в рамках данной задачи. Рассмотрим, например, ситуацию с поставками и продажами пищевых продуктов длительного хранения (крупы, растительное масло и т.п.). Эти товары испытывают сезонные и недельные колебания спроса. Однако период их поставки обычно заметно больше недели, но меньше полугода. В этих условиях для оптимизации поставок мы можем рассматривать средненедельную интенсивность спроса, а оптимизировать поставки в течение каждого сезона в отдельности.
3. Время поставки заказа – известная постоянная величина.
4. Каждый заказ поставляется в виде одной партии.
5. Затраты на осуществление заказа не зависят от размера заказа. Считается, что оформление заявки и документов на получение заказа не зависит от его размеров. От размеров заказа в рамках данной постановки мы считаем независимой и стоимость доставки товара (это предположение, очевидно, справедливо для розничных и мелкооптовых партий товара, умещающихся в одной машине).
6. Затраты на хранение и потери запаса пропорциональны размеру хранимого запаса и времени хранения.
7. Недопустим дефицит товара. То есть товар всегда должен быть в наличии.
Таким образом, в рамках этой модели справедливо:
· 
.
· 
.
· 
.
· 
.
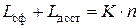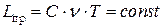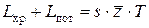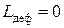где
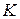– затраты на оформление и доставку одной партии товара (руб.);
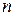– количество партий товара за рассматриваемый интервал времени;
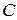– цена за единицу товара (руб./ед.тов.);
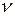– интенсивность (скорость) потребления запаса (ед. тов./ед. времени);
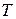– продолжительность рассматриваемого интервала времени (ед. времени);
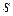– затраты на хранение единицы товара в единицу времени (руб./ед.тов ед. времени.);
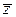– среднее количество запасов (ед.тов.).
Анализ модели Уилсона показывает, что оптимально поставлять товар одинаковыми партиями размера 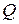. Тогда за рассматриваемый интервал времени 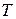будет поставлено товара 
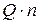. За этот же промежуток времени товар будет потреблен в количестве 
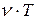. Из условия недопустимости дефицита и нерациональности поставок, превышающих спрос следует условие:
.
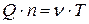Откуда
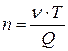. (1)
Заметим, что если мы имеем строго фиксированный промежуток времени 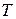, то необходимо потребовать целочисленности числа поставок 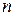. Однако обычно интервал 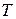задает лишь характерное время анализа (например неделю, месяц и т.п.). В этом случае важна лишь частота поставок и число 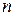может быть нецелочисленным (например 3,2 поставки в неделю означает, что необходимо осуществлять 
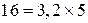поставок за 5 недель).
Уровень запаса товара в данной модели представлен на рис. 2.
 |
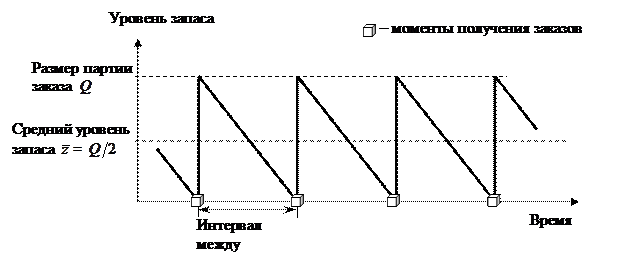Рис. 2. График циклов изменения запасов по модели Уилсона.
тогда затраты за рассматриваемый интервал времени равны
; 
; 
.
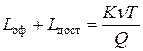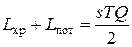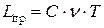
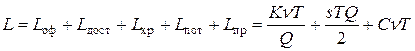Все величины, кроме объема партии 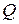, в этих формулах постоянны.
Если потребовать минимума величины совокупных затрат:
,
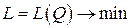то из необходимого условия экстремума
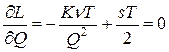
определяем объем оптимальной партии (формула Уилсона):
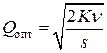. (2)
После этого определяем минимальные совокупные затраты за интервал времени:
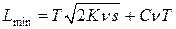
Так как оптимальный запас часто приходится округлять, то минимальные затраты лучше вычислять по общей формуле:
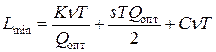(3)
На рис. 3. показаны типовые графики зависимости затрат от объемов поставки для модели Уилсона, полученные по приведенным выше формулам.
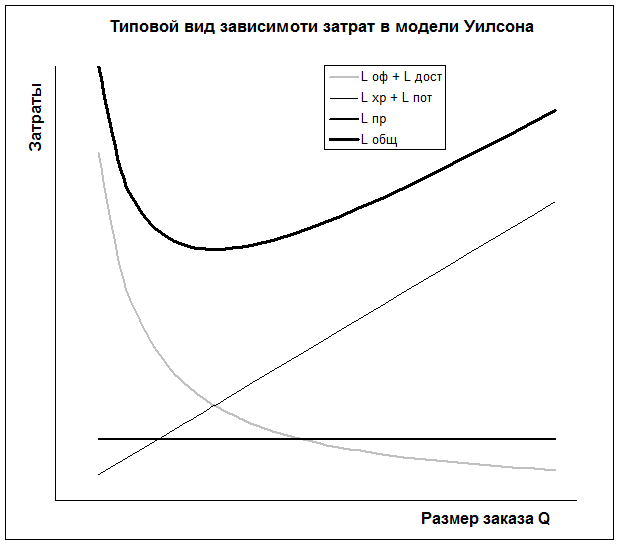
Рис. 3. Зависимость затрат от объема поставки в модели Уилсона
По формуле (1) определяем оптимальное количество поставок за исследуемый интервал времени:
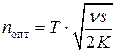, (4)
оптимальную частоту заказов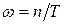 
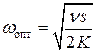, (5)
и интервал между поставками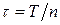 
:
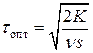(6)
Если время выполнения и доставки заказа равно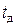 
, то очевидно, необходимо подавать заказ за это время до требуемого момента получения заказа (см. рис. 4). При этом величина запаса в момент подачи заказа 
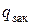(точка заказа) будет равна
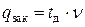. (7)
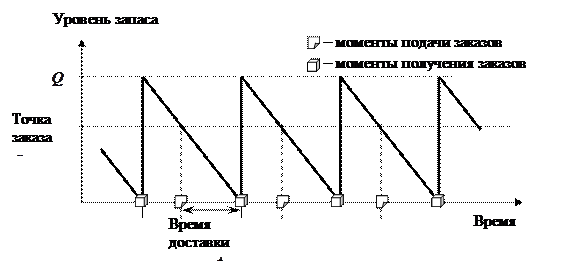
Рис. 4. График циклов изменения запасов по модели Уилсона
с учетом времени доставки.