Понятие о цене информации в игре с природой
В игре с природой часто возникает возможность получения информации или уточнения данных о реализации состояний природы. Такая информация «предоставляется» не «бесплатно» – для ее получения необходимо затратить определенные усилия, вложить средства и т.п.
Встает вопрос о максимальной «цене» такой информации. Сколько мы можем «заплатить» за информацию, чтобы выигрыш при обладании ей за вычетом платы за информацию был не меньше выигрыша без учета этой информации? При этом необходимо сравнивать, очевидно, случаи оптимального поведения при дополнительной информации и без нее.
Проще всего данный вопрос осветить на примере игры с природой, имеющей частые повторения (партии) в одинаковых условиях. В этом случае для выбора оптимальной стратегии предпочтительно использовать критерий Байеса.
В качестве примера рассмотрим следующую ситуацию.
Коммерсант ежедневно возит молочную продукцию на своем автомобиле для продажи в дачном поселке. Он закупает молоко ящиками по 20 бутылок по мелкооптовой цене 20 рублей за бутылку и продает в розницу по 35 рублей за бутылку. За день может быть реализовано от 1 до 5 ящиков. Так как в автомобиле нет холодильника, то все нереализованное молоко портится и выбрасывается. По предварительным опросам дачников, коммерсант делает предположение о вероятностях спроса: спрос в 1 ящик имеет вероятность 10%, в 2 ящика – 20%, в 3 ящика – 30%, в 4 ящика – 30%, в 5 ящиков – 10% (для простоты рассмотрения будем считать, что ежедневно продается целое количество ящиков молока). Таким образом, ежедневно коммерсант должен принять решение, сколько ящиков молока закупить и привезти на продажу.
Запишем матрицу игры с природой для этой задачи. Выигрышем будем считать прибыль, которую получит коммерсант в каждой ситуации. Строки матрицы будут соответствовать возможным стратегиям коммерсанта – купить 1, 2, 3, 4 или 5 ящиков. Столбцы будут соответствовать спросу на молоко: 1, 2, 3, 4 или 5 ящиков. Матрица игры с природой будет иметь представлена в табл. 5.
Поясним, как получились значения в таблице. Как следует из условия, при покупке одного ящика коммерсант тратит 400 руб., а при продаже получает 700 руб. Таким образом, каждый проданный ящик приносит прибыль 300 руб., а каждый пропавший приносит убыток 400 руб. (то есть прибыль минус 400 руб.).
Рассмотрим ситуацию, когда коммерсант привез 4 ящика. Если спрос равен 4 ящикам, то прибыль будет равна 1200 руб. При спросе 3 ящика прибыль составит 500 руб. Для спроса 2 ящика получаем убытки 200 руб. (результат игры равен – 200). Для спроса 1 ящик результат равен – 900 руб. Если же спрос равен 5 ящикам, то продается только 4, так как больше товара нет, и спрос остается неудовлетворенным. В этом случае, как и при спросе, равном 4, результат игры равен 1200 руб. Для других вариантов завоза результаты получаются аналогично.
Таблица 5.
Игра с природой для примера Исполнитель – Заказчик
| Спрос Закупка | 1 ящ. | 2 ящ. | 3 ящ. | 4 ящ. | 5 ящ. |
| 1 ящ. | |||||
| 2 ящ. | – 100 | ||||
| 3 ящ. | – 500 | ||||
| 4 ящ. | – 900 | – 200 | |||
| 5 ящ. | – 1300 | – 600 | |||
Вероятности  | 0,1 | 0,2 | 0,3 | 0,3 | 0,1 |
Если другой информации у коммерсанта нет, то ему лучше применять для выбора стратегии критерий Байеса – в этом случае он сможет оптимизировать среднюю прибыль и добиться наилучшего результата за многодневный период торговли.
Таким образом, лучше возить по 3 ящика молока. Тогда средняя дневная прибыль составит 620 рублей.
Рассмотрим две возможности дополнительной информации:
1. Имеется возможность знать состояние природы перед каждой следующей партией в игре. В данном случае – знать спрос на следующий день (например, можно провести мониторинг спроса на следующий день, организовать продажи по записи и т.п.).
2. Имеется возможность уточнить значения вероятностей состояний природы (например, собрать информацию об аналогичных объектах, провести подробное изучение спроса и т.п.).
Описанные возможности требуют дополнительных затрат средств и времени. Каковы максимально допустимые удельные затраты (затраты в пересчете на один день торговли)?
Изучим первую возможность. Если коммерсант будет точно знать спрос на следующий день, то он привезет оптимально количество молока – ровно столько ящиков, сколько будет закуплено. При этом прибыль составит по 300 руб. с 1 ящика, 600 руб. с 2-х, 900 руб. с 3-х, 1200 руб. с 4-х и 1500 руб. с 5-ти ящиков. Так как знание спроса не влияет на частоту его реализации, то 1 ящик он будет возить 10% дней, 2 ящика – 20%, 3 ящика – 30%, 4 ящика – 30% и 5 ящиков – 10%. В итоге коммерсант получит среднюю прибыль, равную:
руб.
Таким образом, владея информацией о спросе, коммерсант увеличил свою среднюю прибыль на 310 руб. в день. Именно это и есть удельная стоимость точной информации о спросе.
Важно заметить, что в результате получения информации коммерсант принципиально поменял свою деятельность: вместо ежедневного завоза по 3 ящика молока он должен возить различное количество, строго определенное дополнительной информацией.
Изучим второй вид дополнительной информации. Представим, что у коммерсанта имеется противоречивая информация о вероятностях спроса. Первая версия описана выше (0,1; 0,2; 0,3; 0,3; 0,1). По второй версии спрос равновероятен, то есть вероятность спроса равна 0,2 для всех вариантов. Третьи источники утверждают, что спрос в 1, 2, 3, 4 и 5 ящиков имеет вероятности соответственно 0,1; 0,1; 0,1; 0,4; 0,3. Если мы можем провести серию мероприятий по уточнению этой информации, то какова максимальная удельная стоимость таких мероприятий?
Оптимальный выбор стратегии при первом варианте мы уже сделали – нужно возить по 3 ящика и получим в среднем 620 руб. в день.
Для второго варианта вероятностей:
Несмотря на то, что среднее значение прибыли заметно изменилось, выбор стратегии не поменялся. Можно сделать вывод, что уточнение между первым и вторым вариантами вероятностей состояний ничего не стоит. (Это справедливо лишь для поставленной цели определения количества завозимого ежедневно молока. Если же главной целью является оценка рентабельности бизнеса, то цена такой информации может быть совсем ненулевой. Подумайте, почему?).
Для третьего варианта вероятностей:
В данном случае лучше возить по 4 ящика молока и получим в среднем 780 руб. в день прибыли. То есть такая информация побуждает нас сменить решение. Однако посмотрим, сколько же стоит информация с учетом «разумности» нашего поведения при потенциальной возможности первого или третьего вариантов распределения.
Предполагая возможность всех вариантов распределения (а не точную уверенность в одном из них), коммерсант находится в дилемме выбора между 3 и 4 ящиками. Выбрав 4 ящика, в первом случае он получит 500 руб. в день вместо 620 (потеря 120 руб.). Во втором случае он получит 360 руб. вместо 480 (потеря 120 руб.). Выбрав же 3 ящика при третьей возможности вероятностей, он получит 710 руб. вместо 780 (потеря 70 руб.). Таким образом, минимальная потеря достигается выбором 3 ящиков и равна 70 рублям. Это и есть максимальная удельная цена данного уточнения.
Интересно заметить, что оценивая разные варианты, мы фактически применили критерий Сэвиджа к новой матричной игре, в которой состояниями природы являются уже варианты распределения вероятностей, а результатами – средние результаты при данных вероятностях:
Таблица 6.
Вторичная игра с природой для оценивания
результатов при разных распределениях вероятностей
| Вероятности Закупка | 0,1;0,2;0,3;0,3;0,1 | 0,2;0,2;0,2;0,2;0,2 | 0,1;0,1;0,1;0,4;0,3 |
| 1 ящ. | |||
| 2 ящ. | |||
| 3 ящ. | |||
| 4 ящ. | |||
| 5 ящ. |
Максимальная удельная стоимость информации в таком случае оказалась равна минимаксу матрицы рисков для такой игры:
Заметим, что все приведенные рассуждения справедливы в предположении, что уточняя информацию о вероятностях, мы получим один из известных вариантов распределения. Таким образом, выбирая решение без точной информации, мы все же учитывали ее потенциальные возможности. Получение же неожиданного нового варианта распределения считалось невозможным. Оценка стоимости информации о вероятностях состояний природы без фиксации предварительных вариантов – гораздо более сложная задача.
В общем случае можно определить стоимость информации так: стоимость точной информации не может превышать разницу выигрышей, полученную за счет изменения стратегии в результате обладания данной информацией относительно лучшего варианта стратегии при рассмотрении всех возможных вариантов как потенциально реализуемых.
Задание для самостоятельного решения
Числовые условия задания формируются на основе двух последних цифр зачетной книжки или студенческого билета. Выполнение чужого варианта задания не допускается. В задачах данной темы:
;
;
;
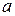– последняя цифра номера зачетной книжки;
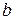– предпоследняя цифра номера зачетной книжки.
Задание
Фирма постоянно поставляет на рынок новинки видеозаписей. Себестоимость одного диска (диск, работа, лицензионные отчисления) равна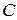 
рублей. В первую неделю продаж диск позиционируется как новинка и продается в собственном магазине по цене 
руб. за штуку. Со второй недели цена дисков резко падает и они передаются в торговые сети по остаточной стоимости 40 руб. за диск. Директор фирмы знает, что за первую неделю возможно продать от 2 до 4 коробок с дисками по 500 штук в каждой. Вероятность спроса равна 30% для 2 коробок, 50% для 3 коробок и 20% для 4 коробок. Если сделать скидку на диски, равную 
%, то вероятность спроса поменяется и будет равна 20% для 2 коробок, 40% для 3 коробок и 40% для 4 коробок.
1. Определить оптимальную стратегию поведения фирмы для оптимизации прибыли. Имеет ли смысл делать скидку на фильмы?
2. Определить, какова максимальная стоимость информации о реальном спросе на конкретную видеозапись? Имеет ли смысл делать скидку в этом случае?
Подсказка: предложения со скидкой и без нее рассмотреть как отдельные возможные стратегии статистика с зависящими от них вероятностями состояний природы.
ТЕМА 2.
Управление запасами.
Детерминированные модели