Кишкинова О.А., Левченкова Т.В., Черенкова И.А.

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«МОСКОВСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ВЕТЕРИНАРНОЙ МЕДИЦИНЫ и БИОТЕХНОЛОГИИ - МВА имени К.И. СКРЯБИНА»

_______________________________________________________________________

Кишкинова О.А., Левченкова Т.В., Черенкова И.А.

МАТЕМАТИКА

Методические рекомендации и

контрольные задания

Москва - 2016

УДК 51 (07)

Кишкинова, О.А. Математика. Методические рекомендации и контрольные задания /. О.А Кишкинова, Т.В. Левченкова, И.А. Черенкова – М.: ФГБОУ ВО МГАВМиБ – МВА имени К.И. Скрябина, 2016. – 58 с.

Приведены: содержание дисциплины «Математика», методические рекомендации, задачи для контрольной работы и список литературы.

Предназначены для студентов факультета зоотехнологии и агробизнеса заочного и очно-заочного (вечернего) отделений по специальности (направление подготовки) 36.03.02. «Зоотехния», квалификация (степень) – бакалавр.

Рецензенты: кандидат биологических наук, профессор кафедры генетики и разведения животных им. В.Ф. Красоты ФГБОУ ВО МГАВМиБ – МВА имени К.И.Скрябина Ф.Р. Бакай.

Утверждено на заседании учебно-методической комиссии факультета зоотехнологий и агробизнеса ФГБОУ ВО МГАВМиБ – МВА имени К.И.Скрябина (протокол № 2 от 13 октября 2016 г).

ВВЕДЕНИЕ

Главная задача дисциплины – подготовить студентов к изучению специальных предметов, в основе которых в значительной степени лежат методы современной математики, привить студентам умение самостоятельно изучать учебную литературу по математике и ее приложениям, повысить уровень логического мышления и математической культуры. Полученные знания позволяют выпускникам академии эффективно применять математические методы исследования и обработки результатов опытов в практической деятельности.

Предлагаемая работа содержит программу, методические указания и контрольные задания по курсу высшей математики.

Основной формой обучения студента-заочника является самостоятельная работа с учебными пособиями, выполнение упражнений, указанных в данных методических указаниях, контрольной работы по всему курсу.

В помощь заочникам в академии организованы чтение лекций и практические занятия. Дополнительную работу проводят в процессе рецензирования контрольных работ. Изучение курса завершается экзаменом.

I. Содержание дисциплины «Математика»

Дифференциальное исчисление функций одной переменной

Понятие функции, его области определения и области значений. Частное значение. График функции. Способы задания функций. Классы элементарных функций, их графики. Примеры неэлементарных функций. Свойства функций: четность, периодичность, монотонность. Сложная функция.

Окрестность точки. Предел функции в точке. Геометрический смысл предела. Односторонние пределы. Бесконечно большие и бесконечно малые функции и их связь с пределами функций. Примеры. Основные теоремы о пределах. Вычисление пределов. Раскрытие неопределенностей вида . Первый замечательный предел.

Непрерывность функции в точке и на промежутке. Теоремы о непрерывных функциях. Непрерывность основных элементарных функций. Непрерывность сложной функции. Асимптоты кривой.

Понятие производной функции одного переменного. Геометрический и физический смыслы. Уравнения касательной и нормали.

Общие правила дифференцирования. Таблицы основных производных.

Производная сложной функции.

Производные и дифференциалы высших порядков.

Правило Лопиталя.

Приложение дифференциального исчисления к биологическим процессам. Примеры. Решение задач физики, биологии, химии с помощью производной и дифференциала.

Дифференциальное исчисление функций одной переменной

Монотонность функции.

Переменную величину называют монотонной, если она изменяется только в одном направлении, т.е. либо только возрастает, либо только убывает. Очевидно, что движение точки х в сторону положительного направления оси абсцисс является мо­нотонно возрастающим, а в противоположную сторону - монотонно убывающим.

Функция у = f(х) называется монотонно возрастающей на интервале (а, b), если для любых х₁, и х₂, при­надлежащих этому интервалу, из неравенства х₂>х₁, следует неравенство f(х₂) >f(x₁) (рис. 3а).

Функция у = f(х) называется монотонно убывающей на интервале (а, b), если для любых х₁и х₂, принад­лежащих этому интервалу, из неравенства х₂>х₁, следует неравенство f(x₂) <f(x₁) (рис. 3б).

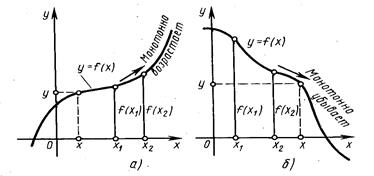
Рис. 3. Графики монотонно возрастающей и монотонно убывающей функций.

Естественно, что интервал (а, b)предполагается взятым из области определения функции.

Выпуклость функции

Говорят, что функция у = f(х) выпукла вверхв точке х₀, если существует окрестность точки х₀такая, что для всех ее точек х касательная к графику функции в точке М₀(х₀, у₀) лежит выше графика (рис. 4а). Говорят, что функция
у = f(х)выпукла внизв точке х₀, если существует окрестность точки х₀такая, что для всех ее точек х касательная к графику функции а точке М₀(х₀; у₀) лежит ниже графика (рис. 4б).

Если на некотором промежутке (а;b) все касательные к гра­фику функции
у = f(х) лежат выше (соответственно ниже) самого графика, то на данном промежутке функция выпукла вверх (со­ответственно выпукла вниз).

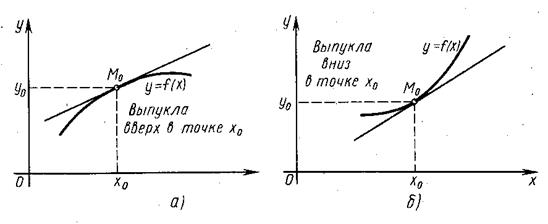
Рис. 4. Графики выпуклой функции

Вопросы для самопроверки:

1. Что называется функцией?

2. Какие способы задания функции Вы знаете?

3. Сформулируйте основные свойства функции.

Предел функции

Число А называется пределом функции в точке х₀ (или при х 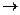х₀), если для любого положительного числа 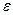найдется такое положительное число 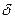( 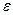), что для всех х 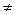х_0, удовлетворяющих неравенству 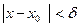, выполняется неравенство .

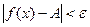Обозначают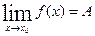

Функция 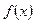называется бесконечно малой при 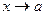, если .

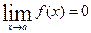Функция 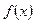называется бесконечно большой при 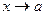, ес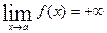ли или .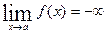

Теоремы о пределах

1.

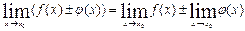
2.

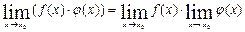
3.

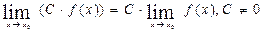
4.

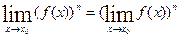
5.

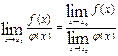
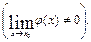
Первый замечательный предел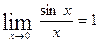

Второй замечательный предел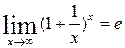

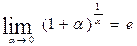
Правила дифференцирования

Производная суммы двух функций:

Производная произведения постоянной и функции:

Производная произведения двух функций:

Производная частного двух функций:

Производная сложной функции:

Таблица производных

1. , ; 2. ,

3. ; 4. ;

5. ; 6. ;

7. ; 8. ;

9. ; 10. ;

11. ; 12. ;

13. ; 14. ;

15. ; 16. ;

Данные производные позволяют дифференцировать всякую сложную функцию, которая представляет собой цепочку основных элементарных функций. Если , то и вышеприведенный перечень упрощается:

1. , ;

2. , ;

3. ; и т.д.

Задача . Найти производную функции .

Решение:

Задача . Найти .

Решение:

Тогда .

Если известна производная функции , то дифференциал функции может быть легко вычислен по формуле: .

Решение: Найдем производную .

Задача. Найти вторую производную функции

Решение: Найдем первую производную функции.

.

Находим вторую производную.

= = .

Задача Найти вторую производную функции

Решение: Находим первую производную:

= .

Находим вторую производную

.

Вопросы для самопроверки:

1. Дайте определение производной функции.

2. Геометрический смысл производной функции.

3. Физический смысл первой и второй производной.

4. Сформулируйте правила дифференцирования.

5. Производная сложной функции.

Экстремумы функции

Пусть функция у = f(х) определена на отрезке [а;b]. Говорят, что функция
у = f(х) имеет локальный максимум в точке х₀ є [а;b], если существует окрестность точки х₀, целиком содержащаяся в [а;b ] и такая, что для любого х, при­надлежащего этой окрестности, выполняется неравенство f(х) <f(х₀).

Говорят, что функция у = f(х) имеет локальный минимум в точке х₀є[а;b], если существует окрестность точки х₀, целиком содержащаяся в [а;b] и такая, что для любого х, принадлежаще­го этой окрестности, выполняется неравенство f(х) >f(х₀).

Правило Лопиталя

Теорема: Пусть функци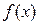и и 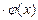непрерывны и дифференцируемы в окрестности точки x₀ и обращаются в нуль в этой точке: 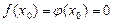, 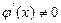в окрестности точки x₀. Если существует предел 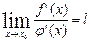, то .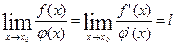

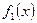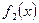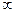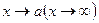Согласно правилу Лопиталя, если функции и одновременно стремится к 0 или при , то .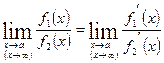

Если отношение производных функций тоже имеет вид 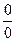или 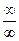, то можно снова применить правило Лопиталя и так несколько раз до получения результата.

Задача. Найти .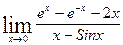

Решение:

При х, стремящемся к 0, числитель и знаменатель стремятся также к 0, т.е. имеем неопределенность вида 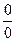и применимо правило Лопиталя:

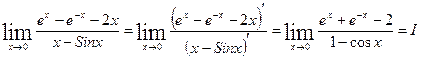
При х, стремящемся к 0, числитель и знаменатель новой дроби стремятся к 0. По правилу Лопиталя:

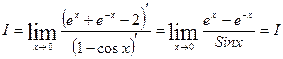
По-прежнему имеем неопределенность вида 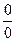, т.к.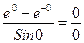

Применяя еще раз правило Лопиталя, получаем:

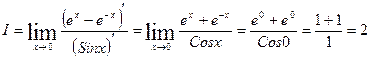
Задача . Вычислить предел с помощью правила Лопиталя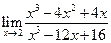

Решение:

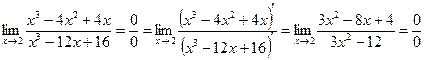
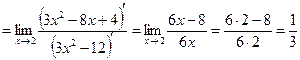
Рассмотренные примеры иллюстрирует тот факт, что правило Лопиталя допустимо применять несколько раз, если отношение производных также представляет собой неопределенность вида 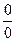или .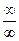

Задача. Вычислить предел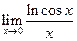

Решение: .

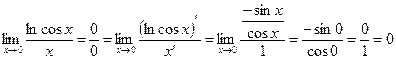Рассмотрим примеры, решение которых существенно упрощается с использованием правила Лопиталя.

Задача .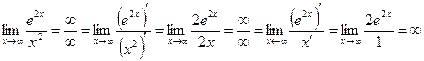

Задача . .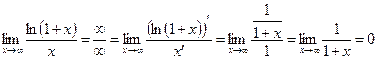

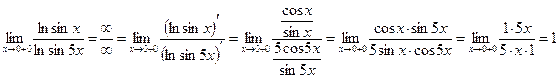
Вопросы для самопроверки:

1. В чем заключается правило Лопиталя?

2. Сформулируйте признаки возрастания и убывания функции.

3. Сформулируйте достаточные условия экстремума функции.

4. Как находятся интервалы выпуклости и вогнутости кривой ?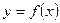

5. Что называется точкой перегиба графика функции?

6. Сформулируйте достаточный признак существования точки перегиба.

Функция двух переменных

Если каждой паре действительных чисел (x; y) из области D по определенному правилу ставится в соответствие только одно число z из области Е, то говорит, что на множестве D задана функция двух переменных

z = z(x, y).

Значение z(a; b) функции z = z (x, y) есть значение этой функции, вычисленное при x = a, y = b.

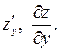Частной производной функции z = z(x, y) по аргументу x называется производная этой функции по x, при постоянномy.

Обозначения:

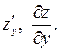Аналогично, частной производной функции z = z(x, y) по аргументу y называется производная этой функции по y при постоянномx.

Обозначения:

При дифференцировании полезна следующая таблица:

Х/Х=1	Х/У=0
У/У=1	У/Х=0
С/Х=0	С/У=0	С - const

Задача :Найти частные производные функции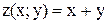

Решение: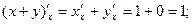

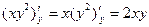
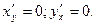
Задача. Найти частные производные функции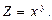

Решение: Найдем производную функции Z по переменной x. В этом случае, при дифференцировании величина y считается постоянной и поэтому: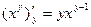

Аналогично найдем производную функции по y, считая величину x постоянной: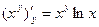

Задача. Найти частные производные z_x', z_y'для функции

z =x³–3x²y+2y³+1,

Решение:

z_x' =(x³–3x²y+2y³+1)_x' =(x³)_x'–(3x²y)_x' +(2y³)_x'+1_x' =3x² -3y(x²)_x' +0+0=3x²–6xy

z_y'=(x³–3x²y+2y³ +1)_y' = (x³)_y'–(3x²y)_y+(2y³)_y'+1_y'=0–3x²y_y'+2(y³)_y'+0=-3x²+6y²

Задача . 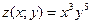. Найт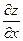и и .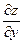

При вычислении частной производной по переменной x заметим, что 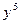является постоянной величиной, а постоянный множитель можно выносить за знак производной. Поэтому имеем

.

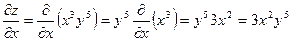Аналогично, при вычислении частной производной по переменной y заметим, что 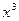является постоянной величиной, а постоянный множитель можно выносить за знак производной. Поэтому имеем

.

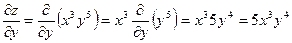Задача. 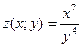. Найт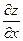и и .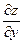

Решение: При вычислении частной производной по x заметим, что 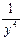является постоянным множителем. Тогда

.

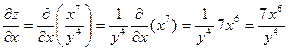Аналогично при вычислении частной производной по y заметим, что 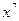является постоянным множителем. Тогда

.

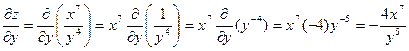Частными производными второго порядка функции z=z(x, y) называются частные производные от частных производных первого порядка.

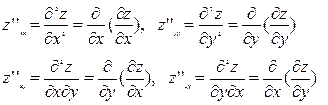Порядок дифференцирования указан в индексе при прочтении слева направо.

Последние две производные отличаются только порядком, называются смешанными и в случае их непрерывности равны.

Задача: Найти все частные производные 2-ого порядка и проверить равенство z¢¢_xy=z¢¢_yxдля функции z=x²-2xy²

Решение: Вначале найдем частные производные первого порядка:

z¢_x=(x²-2xy²)¢_x=2x-2y², z¢_y= (x²-2xy²)¢_y=-4xy

Далее частные производные второго порядка:

z¢¢_xx= (2x-2y²)¢_x= 2, z¢¢_yy= (-4xy)¢_y = -4x

z¢¢_xy= (2x-2y²)¢_y= -4y, z¢¢_yx= (-4xy)¢_x = -4y

Нетрудно видеть, что z¢¢_xy = z¢¢_yx

Выполнение этого условия может служить критерием правильности нахождения частных производных 1-огопорядка и смешанных – 2-ого порядка.

Производная сложной функции

Если z=z(u,v), где u=u(x,y), v=v(x,y), то частная производная функции zпо переменной xи частная производная функции zпо переменной yсоответственно равны:

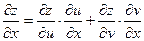
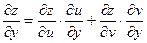
Задача: Найт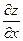и и 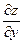, если 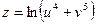, где , .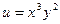

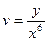Решение:

.

.

.

.

.

.

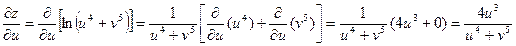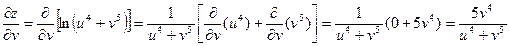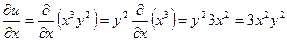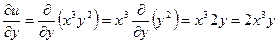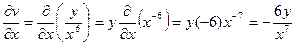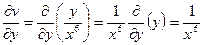Тогда

= + .

= + .

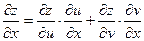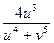
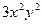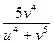
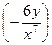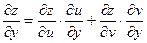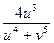
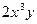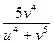
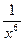Задача. Найти частные производные второго порядка от функции .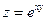

Решение: Сначала найдем частные производные первого порядка:

; .

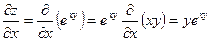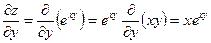Дифференцируя по переменным x и y полученные частные производные 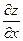и 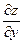, получим:

;

.

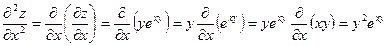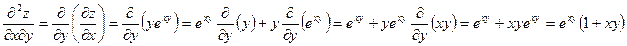
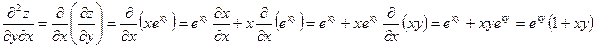
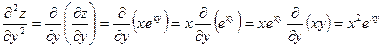Мы получили, что 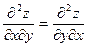. Это совпадение не является случайным. Имеет место важная теорема: Если частные производные (всех порядков) функции непрерывны, то их значения не зависят от порядка дифференцирования.

Ое полезное правило

1. Если , то

Частные случаи:

1.

2.

3.

4.

Задача: Вычислите интеграл

По первому полезному правилу получим:

I=

Ое полезное правило

Задача: Вычислите интеграл

Преобразуем подынтегральное выражение

. По второму полезному правилу получим:

Вопросы для самопроверки.

1. Что называется первообразной?

2. Что называется неопределенным интегралом?

3 Сформулируйте свойства неопределенного интеграла

4 Каковы основные методы интегрирования?

Определенный интеграл

Теорема Ньютона - Лейбница:

Если функция F(x) – какая- либо первообразная от непрерывной функции f(x) на отрезке [a;b], то имеет место равенство:

Задача Найти .

Решение:

Основные понятия

При анализе динамических процессов в различных областях науки и техники часто возникают задачи решения дифференциальных уравнений, которые связывают искомую функцию и её производные различных порядков. Различают обыкновенные дифференциальные уравнения и дифференциальные уравнения в частных производных.

Дифференциальное уравнение называется обыкновенным, если оно содержит искомую функцию от одной переменной, её производные различных порядков и независимую переменную. Общий вид обыкновенного дифференциального уравнения определяется следующим выражением: Если в уравнении искомая функция зависит от нескольких переменных и это уравнение содержит частные производные, то такое уравнение называется дифференциальным уравнением в частных производных. Порядком дифференциального уравнения называется порядок наивысшей производной, входящих в уравнение.

Задача нахождения первообразной - функции, производная которой при каждом значении равна заданной функции 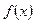, - может быть записана как простейшее обыкновенное дифференциальное уравнение первого порядка: .

Любая функция , обращающая уравнение при в тождество, может быть выражена с использованием неопределенного интеграла . Здесь и далее - какая-либо одна из первообразных функции 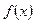, С – произвольная постоянная.

Обыкновенным дифференциальным уравнением первого порядканазывается уравнение вида , где F– функция от трех переменных.

Уравнение , где - функция, определённая в некоторой области D плоскости Оху, называют дифференциальным уравнением первого порядка, разрешенным относительно производной. Предполагается, что функция является непрерывной.

Решением дифференциального уравнения на некотором интервале называется функция , определенная и дифференцируемая на этом интервале и удовлетворяющая следующим двум условиям:

1) точка при любом ;

2) при любом .

Решить (проинтегрировать) дифференциальное уравнение -

значит, найти все его решения в заданном конечном или бесконечном интервале .

Интеграл дифференциального уравнения - решение этого уравнения, заданное в неявном виде.

График решения дифференциального уравнения на плоскости Оху называется интегральной кривой.

Задача Коши при решении дифференциального уравнения заключается в следующем: требуется найти его решение, удовлетворяющее начальному условию , где .

Пусть задано дифференциальное уравнение . Если функция и её частная производная определены и непрерывны в некоторой области D, и точка ,то существует единственное решение уравнения , удовлетворяющее начальному условию .

Общим решением дифференциального уравнения в некоторой области называется функция ,зависящая от переменной х и одной произвольной постоянной С (параметра), если:

1) является решением уравнения при любом допустимом значении постоянной С;

2) при любом начальном условии , удовлетворяющем условию , существует единственное значение параметра такое, что функция удовлетворяет условию .

Частным решением дифференциального уравнения в некоторой области называется функция , которая получается из общего решения уравнения в области G при конкретном значении произвольной постоянной .

Список литературы

1. Антонов, В.И. Элементарная математика для первокурсника: учеб. пособие для студентов вузов/ В.И. Антонов, Ф.И. Копелевич. - СПб.; М.; Краснодар: Лань, 2013. - 101 с.: граф., рис.. - (Учебники для вузов. Спец. лит.). - Библиогр.: с. 99.

2. Кузнецов, Л.А. Сборник заданий по высшей математике. Типовые расчеты: учеб. пособие для студентов вузов. По напр. подгот. и спец. в области естественных наук и мат., техники и технологий, образования и пед. / Л.А. Кузнецов. - 12-е изд., испр.. - СПб.; М.; Краснодар: Лань, 2013. - 238 с.: табл.. - (Учебники для вузов. Спец. лит.)

3. Назаров, А.И. Курс математики для нематематических специальностей и направлений бакалавриата: учеб / А.И. Назаров, И.А. Назаров. - СПБ: Лань, 2011.- 576 с

.

Содержание

ВВЕДЕНИЕ. 3

I. Содержание дисциплины «Математика». 3

1.1 Дифференциальное исчисление функций одной переменной. 3

1.2 Дифференцирование функций нескольких переменных. 4

1.3 Интегральное исчисление функций одной переменной. 4

1.4 Обыкновенные дифференциальные уравнения. 5

1.5 Элементы теории вероятностей и математической статистики. 5

II. Методические указания по изучению курса дисциплины «Математика». 7

2.1 Дифференциальное исчисление функций одной переменной. 7

2.1.1 Понятие числовой функции. Свойства функции. 7

2.1.2 Предел функции. 11

2.1.3 Производная функции одного переменного. 19

2.1.4 Приложения дифференциального исчисления к исследованию функции 23

2.1.5 Правило Лопиталя. 27

2.2 Дифференциальное исчисление функции двух переменных. 30

2.2.1 Функция двух переменных. 30

2.2.2 Производная сложной функции. 32

2.2.3 Экстремум функции двух переменных. 34

2.3 Интегральное исчисление функции одной переменной. 36

2.3.1 Первообразная. Неопределенный интеграл. 36

2.3.2 Определенный интеграл. 42

2.3.3 Приложения определенного интеграла. 44

2.4 Обыкновенные дифференциальные уравнения. 46

2.4.1 Основные понятия. 46

2.4.2 Дифференциальные уравнения первого порядка с разделяющимися переменными. 48

2.4.3 Простейшие дифференциальные уравнения n – го порядка, допускающие понижение порядка методом интегрирования обеих частей уравнения. 50

2.4.4 Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. 50

III. Задачи для контрольной работы.. 50

Список литературы.. 50

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«МОСКОВСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ВЕТЕРИНАРНОЙ МЕДИЦИНЫ и БИОТЕХНОЛОГИИ - МВА имени К.И. СКРЯБИНА»

_______________________________________________________________________

Кишкинова О.А., Левченкова Т.В., Черенкова И.А.

МАТЕМАТИКА

Методические рекомендации и

контрольные задания

Москва - 2016

УДК 51 (07)

Кишкинова, О.А. Математика. Методические рекомендации и контрольные задания /. О.А Кишкинова, Т.В. Левченкова, И.А. Черенкова – М.: ФГБОУ ВО МГАВМиБ – МВА имени К.И. Скрябина, 2016. – 58 с.

Приведены: содержание дисциплины «Математика», методические рекомендации, задачи для контрольной работы и список литературы.

Предназначены для студентов факультета зоотехнологии и агробизнеса заочного и очно-заочного (вечернего) отделений по специальности (направление подготовки) 36.03.02. «Зоотехния», квалификация (степень) – бакалавр.

Рецензенты: кандидат биологических наук, профессор кафедры генетики и разведения животных им. В.Ф. Красоты ФГБОУ ВО МГАВМиБ – МВА имени К.И.Скрябина Ф.Р. Бакай.

Утверждено на заседании учебно-методической комиссии факультета зоотехнологий и агробизнеса ФГБОУ ВО МГАВМиБ – МВА имени К.И.Скрябина (протокол № 2 от 13 октября 2016 г).

ВВЕДЕНИЕ

Главная задача дисциплины – подготовить студентов к изучению специальных предметов, в основе которых в значительной степени лежат методы современной математики, привить студентам умение самостоятельно изучать учебную литературу по математике и ее приложениям, повысить уровень логического мышления и математической культуры. Полученные знания позволяют выпускникам академии эффективно применять математические методы исследования и обработки результатов опытов в практической деятельности.

Предлагаемая работа содержит программу, методические указания и контрольные задания по курсу высшей математики.

Основной формой обучения студента-заочника является самостоятельная работа с учебными пособиями, выполнение упражнений, указанных в данных методических указаниях, контрольной работы по всему курсу.

В помощь заочникам в академии организованы чтение лекций и практические занятия. Дополнительную работу проводят в процессе рецензирования контрольных работ. Изучение курса завершается экзаменом.

I. Содержание дисциплины «Математика»