Следствие о матрице сопряженного оператора в ортонормированном

Базисе

Пусть V _ пространство со скалярным произведением, P _

ортонормированный базис в V, A _ линейный оператор в V, имеющий в

базисе P матрицу A, а A∗ _ сопряженный к A оператор в V, имеющий в

базисе P матрицу A′. Тогда A′ = A⊤.

Определение

Если A _ матрица над полем C, то матрица A⊤ называется эрмитово

сопряженной к матрице A и обозначается A∗.

ение о собственных векторах самосопряженного оператора

Собственные векторы самосопряженного оператора, относящиеся к его

различным собственным значениям, ортогональны.

Доказательство. Пусть A _ самосопряженный оператор, а x и y _

собственные векторы оператора A, относящиеся к его различным

собственным значениям _1 и _2 соответственно. Учитывая, что, в силу

предложения о собственных значениях самосопряженного оператора, _2 _

действительное число, имеем

A(x) ・ y = (_1x)y = _1(xy) и x ・ A(y) = x(_2y) = _2(xy) = _2(xy).
Метод Лагранжа приведения квадратичной формы к каноническому виду

Для приведения квадратичной формы 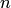переменных к каноническому виду нужно выполнить следующие действия.

1. Выбрать такую переменную (ведущую), которая входит в квадратичную форму во второй и в первой степени одновременно (если в квадратичной форме есть член с квадратом переменной и с произведением этой переменной на другую переменную), и перейти к пункту 2.

Если в квадратичной форме нет ведущих переменных, то выбрать пару переменных, произведение которых входит в квадратичную форму с отличным от нуля коэффициентом, и перейти к п.3.

Если в квадратичной форме отсутствуют произведения различных переменных, то никаких преобразований делать не надо, так как она уже имеет канонический вид.

2. По ведущей переменной выделить полный квадрат: собрать в квадратичной форме все члены с ведущей переменной, дополнить сумму этих членов до полного квадрата (разумеется, добавленные члены нужно также и вычесть, чтобы не изменилась сумма). Получим сумму полного квадрата некоторой линейной формы (в которую входит ведущая переменная) и квадратичной формы, в которую ведущая переменная не входит. Сделать замену переменных: линейную форму, содержащую ведущую переменную, принять за одну из новых переменных, а все старые переменные, за исключением ведущей, принять за соответствующие новые. Продолжить преобразования с пункта 1.

3. Выбранную пару переменных заменить на разность и сумму двух новых переменных, а остальные старые переменные принять за соответствующие новые переменные. При этом произведение пары выбранных переменных преобразуется к разности квадратов двух новых переменных, т.е. в новой квадратичной форме 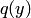будут квадраты переменных с отличными от нуля коэффициентами. Продолжить преобразования новой квадратичной формы с пункта 1.

Идея метода Лагранжа состоит в том, что прием, используемый в п.2 (выделение полного квадрата), исключает одну переменную из числа ведущих. Например, если переменная 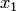— ведущая (т.е. 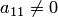и хотя бы один из коэффициентов 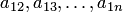отличен от нуля), то выделяем полный квадрат по переменной 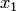(собираем все члены с 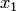и дополняем их сумму до полного квадрата):

Выражение, стоящее в квадратных скобках, есть полный квадрат. Поэтому

где — квадратичная форма, в которую не входит ведущая переменная 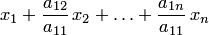— линейная форма, содержащая ведущую переменную 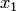. Обозначим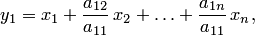 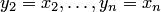, или, что то же самое, сделаем линейную замену переменных:

Тогда данная квадратичная форма преобразуется к виду .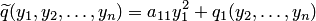

24 вопрос

Преобразование координат точки при замене системы координат? Линейные отображения. Линейные операторы, связанные с линейными отображениями?. Геометрические свойства линейных отображений?. Аффинные и изометрические отображения.

Лине́йное отображе́ние, лине́йный опера́тор — обобщение линейной числовой функции (точнее, функции 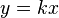) на случай более общего множества аргументов и значений. Линейные операторы, в отличие отнелинейных, достаточно хорошо исследованы, что позволяет успешно применять результаты общей теории, так как их свойства не зависят от природы величин.

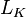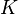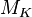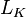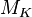Лине́йным отображе́нием векторного пространства над полем в векторное пространство (лине́йным опера́тором из в ) над тем же полем 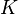называется отображение

,

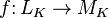удовлетворяющее условию линейности

,

.

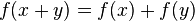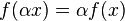для всех 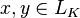и .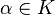

Пространство линейных отображений

Если определить операции сложения и умножения на скаляр из основного поля 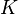как

•

•

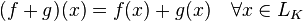
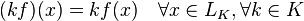
множество всех линейных отображений из 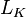в 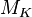превращается в векторное пространство, которое обычно обозначается как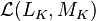

Аффинное отображение

Линейные отображения пространства 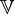в пространство 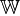являются подмножеством более широкого класса отображений.

Рассмотрим пример 5 ☞ ЗДЕСЬ. Отображение пространства 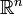в пространство 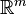, задаваемое соотношением

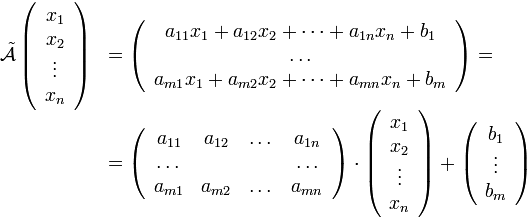
будет линейным отображением при условии, что 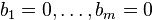и не будет линейным отображением при хотя бы одном из чисел 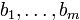отличном от нуля. Тем не менее, по своему внешнему виду отображение из 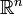в 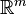, задаваемое в матричном виде как 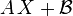очень напоминает линейную функцию 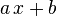, действующую в 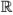. Кажется очень несправедливым лишать подобные отображения эпитета линейный, однако же именно это и произошло в линейной алгебре и геометрии.

Аффинным5) отображением линейного векторного пространства 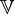с операцией сложения векторов, обозначаемой 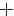, в линейное векторное пространство с операцией сложения векторов, обозначаемой 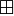, называется функция вида

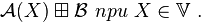
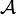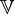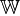Здесь — линейное отображение в , а 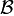— некоторый вектор пространства .

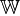Теорема. Аффинное отображение отображает произвольное линейное многообразие пространства 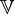в линейное же многообразие пространства 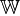. Аффинное отображение отображаетпараллельные многообразия пространства 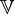в параллельные же многообразия пространства .

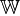Аффинное отображение отображает произвольную прямую пространства 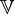в прямую или точку пространства .

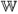Изометрические преобразования

Аффинное преобразование называется изометрическим, если оно сохраняет расстояния между точками.

Рассмотрим любые три точки 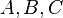, не лежащие на одной прямой. Пусть точки 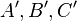получены из них при помощи изометрического преобразования. Так как расстояния между точками не изменилось, то 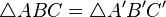Отсюда следует, что изометрическое преобразование не меняет углы между прямыми.

Теорема Матрица изометрического преобразования ортогональна. Доказательство[показать]

Преобразование ортогональных систем координат[править]

Преобразование на плоскости[править]

Преобразование в некоторой прямоугольной системе координат, заданное формулами

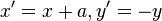называется скользящей симметрией.

Теорема Всякая изометрия плоскости является либо параллельным переносом, либо поворотом относительно некоторой точки, либо скользящей симметрией. Доказательство[показать]

Преобразования в пространстве[править]

Преобразования, заданные формулами

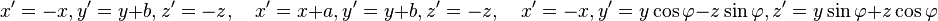называются винтовым вращением, скользящей симметрией и зеркальным вращением соответственно.

Теорема Всякая изометрия пространства является одним из следующих преобразований: 1. винтовое вращение 2. скользящая симметрия 3. зеркальное вращение

25 вопрос.

Прямоугольная система координат на плоскости. Расстояние между точками. Деление отрезка в данном отношении.

Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат 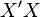и 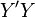(крестом). Оси координат пересекаются в точке 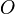, которая называется началом координат, на каждой оси выбрано положительное направление.

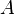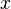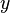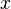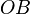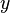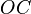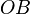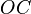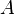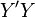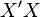Положение точки на плоскости определяется двумя координатами и . Координата равна длине отрезка , координата — длине отрезка в выбранных единицах измерения. Отрезки и определяются линиями, проведёнными из точки параллельно осям и соответственно.

При этом координате 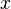приписывается знак минус, если точка 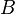лежит на луче 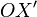(а не на луче 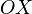, как на рисунке). Координате 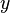приписывается знак минус, если точка 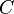лежит на луче 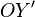. Таким образом, 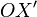и 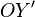являются отрицательными направлениями осей координат (каждая ось координат рассматривается как числовая ось).

Ось 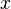называется осью абсцисс, а ось 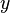- осью ординат. Координата 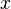называется абсциссой точки 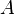, координата 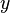— ординатой точки .

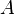Символически это записывают так:

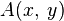
или

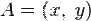
или указывают принадлежность координат конкретной точке с помощью индекса:

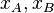
и т. д.

• В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси 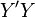вверх, ось 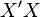смотрела направо. Обычно принято пользоваться правосторонними системами координат (если обратное не оговорено или не очевидно — например, из чертежа; иногда по каким-то соображениям бывает удобнее всё же пользоваться левосторонней системой координат).

• Четыре угла (I, II, III, IV; 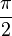), образованные осями координат 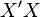и 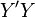, называются координатными углами, четвертями или квадрантами (см. рис. 1).

• Точки внутри координатного угла I имеют положительные абсциссы и ординаты.

• Точки внутри координатного угла II имеют отрицательные абсциссы и положительные ординаты.

• Точки внутри координатного угла III имеют отрицательные абсциссы и ординаты

• Точки внутри координатного угла IV имеют положительные абсциссы и отрицательные ординаты.

Определение.

Расстояние между двумя точками — это длина отрезка, что соединяет эти точки.

Формулы вычисления расстояния между двумя точками:

• Формула вычисления расстояния между двумя точками A(x_a, y_a) и B(x_b, y_b) на плоскости:

AB = √(x_b - x_a)² + (y_b - y_a)²

• Формула вычисления расстояния между двумя точками A(x_a, y_a, z_a) и B(x_b, y_b, z_b) в пространстве:

AB = √(x_b - x_a)² + (y_b - y_a)² + (z_b - z_a)²

26 вопрос.

Общее уравнение прямой на плоскости. Различные способы задания прямой на плоскости.

Общее уравнение

Ax + By + C ( > 0).

Вектор = (А; В) - нормальный вектор прямой.

В векторном виде: + С = 0, где - радиус-вектор произвольной точки на прямой.

Частные случаи:

1) By + C = 0 - прямая параллельна оси Ox;

2) Ax + C = 0 - прямая параллельна оси Oy;

3) Ax + By = 0 - прямая проходит через начало координат;

4) y = 0 - ось Ox;

5) x = 0 - ось Oy.

27 вопрос.

Параметрическое и каноническое уравнения прямой.

уравнение вида называют каноническим уравнением прямой на плоскости в прямоугольной системе координат Oxy. Уравнение также называют уравнением прямой в каноническом виде.

Уравнения полученной системы называются параметрическими уравнениями прямой на плоскости в прямоугольной системе координат Oxy. Смысл такого названия прост: координаты всех точек прямой могут быть вычислены по параметрическим уравнениям прямой на плоскости вида при переборе всех действительных значений параметра .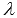

28 вопрос.

Угол между двумя прямыми. Условие параллельности и перпендикулярности прямых.

Условия па Пусть в пространстве заданы две прямые. Их параметрические уравнения:

l1: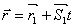

l2: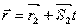

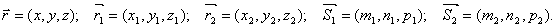
Угол между прямыми ϕ и угол между направляющими векторами ϕ этих прямых связаны соотношением: ϕ = ϕ1 или ϕ = 1800 - ϕ1. Угол между направляющими векторами находится из скалярного произведения. Таким образом:

.

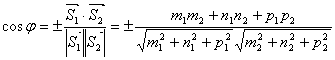раллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k₁ = k₂. (8)

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

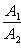
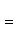
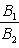
(9)

5 Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

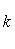
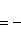
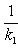
29 вопрос.

Расстояние от точки до прямой. Преобразование координат точки при замене системы координат.

Расстояние от точки до прямой. Преобразование координат точки при замене системы координат

Преобразование координат — замена системы координат на плоскости, в пространстве или, в самом общем случае, на заданном 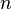-мерном многообразии.

Пример перехода от полярных координат 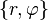к декартовым 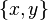на евклидовой плоскости:

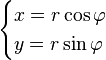
Чаще всего преобразование координат производится для перехода к более простой или более удобной для анализа математической модели. Например, уравнения некоторых плоских кривых в полярных координатах существенно проще, чем в декартовых, а для исследования осесимметричных тел удобно направить одну из осей координат вдоль оси симметрии.

Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.