Вычисление ошибок прямых измерений
Ошибки измерений классифицируют как систематические, случайные и грубые промахи.
Систематическими называют такие ошибки, которые возникают из-за известных причин, действующих по определённым законам и, как правило, в определённом направлении. Их можно количественно определить и вносить в измерения соответствующие поправки.
Случайными называют такие ошибки, причины которых неизвестны и которые невозможно учесть заранее. Такие ошибки можно выразить несколькими способами. Часто пользуются понятием предельной ошибки  , под которой понимают наибольшую случайную ошибку при пользовании исправным прибором при устранённых систематических ошибках. Она может быть определена из паспорта прибора или принята равной половине наименьшего деления шкалы прибора.
, под которой понимают наибольшую случайную ошибку при пользовании исправным прибором при устранённых систематических ошибках. Она может быть определена из паспорта прибора или принята равной половине наименьшего деления шкалы прибора.
При определении величины случайных ошибок можно пользоваться статистической ошибкой, полученной неоднократными измерениями обработкой результатов методами математической статистики. В этом случае последовательность определения случайных ошибок следующая:
1) Прибором измеряют несколько раз (n раз) практически постоянную величину и находят её среднее арифметическое:
 (9)
(9)
2) Вычисляют исправленную дисперсию измеряемой величины:
 (10)
(10)
и исправленное среднее квадратическое отклонение (стандарт):
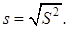 (11)
(11)
3) Тогда наибольшая возможная статистическая ошибка с
вероятностью 99,73% в случае нормального закона распределения случайной величины будет:
 (12)
(12)
а относительная ошибка:
 (13)
(13)
Пример. Определение погрешности прямых измерений (вычисления выполнять с точностью до двух знаков после запятой)
Даны результаты 10 равноточных измерений некоторой физической величины, проведенные без систематических ошибок. Вычислить
1) среднее значение измеряемой величины;
2) среднеквадратическую ошибку;
3) предельную относительную вероятностную ошибку, предполагая, что результаты измерений распределены нормально;
4) доверительный интервал для истинного значения измеряемой величины с надежностью  =0,9.
=0,9.
Результаты измерений:
7,94 8,45 9,09 8,71 8,39 9,37 9,26 8,68 8,28 8,39
1) Найдём среднее арифметическое по формуле (9):

2) Вычислим исправленную дисперсию по формуле (10) и исправленное среднее квадратическое отклонение по формуле (11):

 Итак, среднеквадратическая ошибка равна 0,46
Итак, среднеквадратическая ошибка равна 0,46
3) Вычислим предельную ошибку по формуле (12) и относительную ошибку по формуле (13):


Окончательно результат измерений представляем в виде:
 относительная ошибка составляет
относительная ошибка составляет 
4) Доверительный интервал для среднего значения измеряемой величины найдём по формуле (8). Сначала по таблице [1] найдём критическую точку распределения Стьюдента с числом степеней свободы  и уровнем значимости
и уровнем значимости  Получим t = 1,83 и подставим в формулу (8):
Получим t = 1,83 и подставим в формулу (8):
 . После вычисления получим доверительный интервал для среднего значения
. После вычисления получим доверительный интервал для среднего значения 
