Лекция №2 Связи их реакции. Система сходящихся сил

Лекция №2 Связи их реакции. Система сходящихся сил

П 1. Понятие о связях

Встречаются случаи, когда тело может иметь любые перемещения в пространстве, такое тело мы называем свободным, а если не всякие перемещения разрешаются, то тело называется не свободным. Вот эти ограничения называются связями.

Запишем определение.

Ограничения, налагаемые на перемещение тела, выполняющиеся при любых действующих силах, называется связями.

Материально связи осуществляются в виде некоторых тел.

Связями могут быть поверхности, нити, канаты, ремни, цепи стержни подшипники, подпятники.

Теперь свободным телом можно назвать тело, на которое не наложены никакие связи. Тело, на которое наложены какие-то связи, называется не свободным.

Рассмотрим примеры простейших связей.

Пример № 1

Какие перемещения может это тело совершать?

Оно может, как угодно перемещаться в плоскости стола, а перемещения перпендикулярно вниз уже не разрешаются. Тело не свободное.

Пример №2

На тросе подвешено какое-то тело.

На рисунке: - нить нерастяжима и тело абсолютно твердое

Сила, с которой связь действует на несвободное тело, называется силой реакции или просто реакцией

Вернемся к примеру № 1

= -

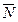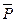
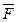- сила давления на связь (действие)

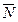- сила реакции связи (противодействие)

В этой задаче легко показать направление реакции.

Все силы действия на несвободное тело принято разделять на две группы

- активные (задаваемые, заданные)

- реакции связи (пассивные силы)

К активным силам относятся силы, которые вызывают движение тела или стремятся вызывать движение тела.

Аксиома № 6 аксиома связей

Принцип освобождаемости от связей

Всякое несвободное тело можно освободить от связей, заменив их действие реакциями, и рассматривать тело как свободное, находящееся под действием приложенных сил и реакций связи.

В чем значение этой аксиомы? Задачу о равновесии не свободного тела мы сводим к задаче о равновесии тела свободного. При этом нельзя забывать, к активным силам присоединять реакции связей.

Реакция шарнира направлена по прямой, перпендикулярной оси шарнира, и лежит в плоскости перпендикулярной к этой оси.

Для уменьшения трения между поверхностями втулки и пальца (болта), применяют различные смазки. Шарнир при отсутствии трения, называют идеальным.

Поскольку мы не знаем заранее направление этой реакции, и ее модуль, то часто при решении задач реакцию R изображают в виде двух составляющих параллельных координатным осям. , .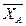

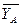Шарнирно - неподвижная опора – ШНО

Все выше перечисленное справедливо для опорного подшипника.

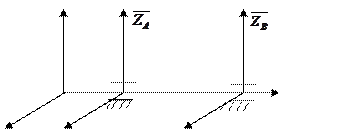z

0 А В y

x

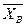
Литература Прусов В М «Статика»

Стр. 37-36 п. 2.4.7. Невесомый стержень шарнирно закрепленный по концам.

Теорема: Система сходящихся сил эквивалентна одной силе, т.е. имеет равнодействующую, равную геометрической сумме сил этой системы.

Т.е.

S( )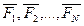

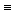
Вопрос:

Как будем доказывать? У нас есть аксиомы статики, с помощью которых мы можем доказать эту теорему. Какая из аксиом нам нужна?

Ответ:

Аксиома №3 Аксиома параллелограмма сил.

Вопрос:

О чем она говорит?

Ответ:

О том, что две силы, приложенные в одной точке можно заменить одной силой по правилу параллелограмма.

Применяем аксиому № 3

Док-во: Сначала складываем по правилу параллелограмма первую и вторую силы, равнодействующую двух сил складываем с третей силой и т.д. Все силы переберем и получим одну силу , которая будет выражаться как векторная сумма. Вместо параллелограмма сил можно построить треугольники. К первой силе приложить второй вектор и соединить начало и конец и т.д.

= =

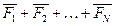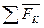
Строить параллелограммы и треугольники дело не слишком приятное. Если много сил, то необходимо строить много треугольников или параллелограммов.

Вопросы:

Как можно этот процесс ускорить? Как можно построить сумму нескольких векторов? Как будет называться фигура построения?

Ответ:

Получится многоугольник из сил системы, а замыкающая сторона будет изображать сумму.

Запишем.

Вместо построения параллелограммов для построения можно построить силовой многоугольник. Он строиться в стороне в выбранном масштабе

.

.

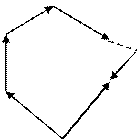
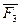
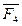
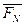
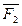
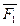
Вопрос:

Всегда ли удобно строить многоугольники?

Причем

=

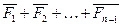
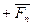
Где

=

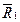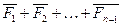
Причем

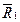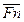= + (6)

По условию S( 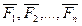) 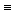0;

По аксиоме №1

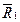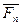, - должны иметь общую линию действия

= -

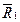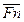
Тогда из (6)

=0

Что и требовалось доказать.

Из условия (5) можно получить векторное условие равновесия для сил данной системы S( ).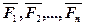

Векторное условие

Т.к.

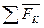= , то

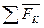=0 (7)

Это необходимое и достаточное условие для равновесия такой системы записанное в векторной форме.

Геометрическое условие

Вспомним геометрический способ нахождения равнодействующей.

Это построение замыкающей стороны силового многоугольника

Для системы находящейся в равновесии =0. конец последней силы должен совпадать с началом первой.

Запишем.

Замечание .

Если линии действия трех сил плоской системы пересекаются в одной точке, то система из этих сил не обязательно будет уравновешенной. Другими словами, обратная теорема несправедлива.

Лекция №2 Связи их реакции. Система сходящихся сил

П 1. Понятие о связях

Встречаются случаи, когда тело может иметь любые перемещения в пространстве, такое тело мы называем свободным, а если не всякие перемещения разрешаются, то тело называется не свободным. Вот эти ограничения называются связями.

Запишем определение.