В чем состоит проблема идентификации модели линейных одновременных уравнений?

Нахождение коэффициентов структурной формы модели после численного нахождения коэффициентов приведенной формы модели не всегда однозначно. При переходе от приведенной формы модели к структурной возникает проблема идентификации модели.

Все типы структурных моделей можно подразделить на три вида:

1) Идентифицируемые (если все структурные коэффициенты однозначно определяются по коэффициентам приведенной формы модели, D = H – 1);

2) Неидентифицируемые (если число приведенных коэффициентов меньше числа структурных коэффициентов, D < H - 1);

3) Сверхидентифицируемые (если число приведенных коэффициентов больше числа структурных коэффициентов, D > H - 1).

Структурное уравнение является идентифицируемым, если идентифицируемы все его коэффициенты. Если хотя бы один из них неидентифицируем, то и все уравнение является неидентифицируемым.

Структурная модель является идентифицируемой, если каждое ее уравнение идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель является неидентифицируемой.

63. Множественная линейная регрессия. Проблема мультиколлинеарности.

При вычислении параметров уравнения множественной регрессии по формулам (3.9), (3.17) и (3.21) необходимо находить матрицу обратную ковариационной S^-1, корреляционной R^-1 или произведению матрицы плана (D'D) ^-1, вычисляемых для независимых признаков. Однако, как следует из теории, операция обращения матрицы возможна только если ее определитель не равен нулю. В частности, если среди набора признаков, для которых вычислены матрицы S, R или D'D имеется хотя бы одна пара показателей, для которой коэффициент корреляции равен +1 или -1, их определители будут равны нулю, и операция обращения этих матриц окажется невозможной. Напротив, для набора нескоррелированных признаков определитель корреляционной матрицы достигнет своего максимального значения ½R½ = 1. В реальных случаях, когда все признаки имеют коэффициенты корреляции 0 < ½r½ < 1, обычно будет наблюдаться ситуация 0 < ½R½ < 1.

Однако, если среди набора независимых переменных X имеются признаки, связанные друг с другом высокой корреляцией с абсолютной величиной ее коэффициента близкой к 1, определители матриц S, R или D'D будут иметь малую величину. Хотя при этом нахождение S^-1, R^-1 или D'D^-1 будет возможным, точность всех вычислений в регрессионном анализе резко уменьшится. Эта ситуация называется явлением мультиколлинеарности.

Наличие мультиколлинеарности приводит к резкой неустойчивости получаемых оценок параметров уравнений регрессии. Добавление или исключение какого-то отдельного наблюдения может приводить к сильному изменению всех регрессионных параметров. Очень сильно при этом могут также увеличиваться квадратические ошибки коэффициентов множественной регрессии, что приведет к невозможности доказать неслучайность.

64. Необходимое условие идентификации модели линейных одновременных уравнений.

Счетное правило – необходимое условие

Если обозначить число эндогенных переменных в j–м уравнении системы через H, а число экзогенных (предопределенных) переменных, которые содержатся в системе, но не входят в данное уравнение, – через D, то условие идентифицируемости модели может быть записано в виде следующего счетного правила:

Если D + 1 = H, то уравнение скорее всего идентифицируемо,

если D + 1 < H, то уравнение неидентифицируемо,

если D + 1 > H, то уравнение сверхидентифицируемо.

Предположим, рассматривается следующая система одновременных уравнений:

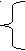y₁ =b₁₂∙y₂+b₁₃∙y₃+a₁₁∙x₁+a₁₂∙x₂,

y₂=b₂₁∙y₁+a₂₁∙x1+a₂₂∙x2+a₂₃∙x₃,

y₃=b₃₁∙y1+b₃₂∙y2+a₃₃∙x3+a₃₄∙x₄.

Первое уравнение скорее всего точно идентифицируемо, ибо в нем присутствуют три эндогенные переменные – y₁, y₂, y₃, т.е. H = 3 и две экзогенные переменные – x₁и x₂, число отсутствующих экзогенных переменных равно двум – x₃и x₄, D = 2. Тогда имеем равенство: D+1 = H, (так как 2+1 = 3), что означает, что это уравнение является подозрительным на то, что оно точно (просто) идентифицируемого уравнения. Для окончательного вывода нужно проверить достаточное условие.

Во втором уравнении системы H = 2 (y₁и y₂) и D = 1 (x₄). Выполняется равенство D+1 = H, т.е. 1+1=2. Уравнение скорее всего идентифицируемо.

В третьем уравнении системы H = 3 (y₁, y₂, y₃), а D=2 (x₁и x₂). Следовательно, по счетному правилу D+1 = H, и это уравнение скорее всего идентифицируемо. Таким образом, система в целом удовлетворяет необходимому условию идентифицируемости.

65. Множественная линейная регрессия. Методы определения мультиколлинеарности.

Существует несколько признаков, по которым может быть установлено наличие мультиколлинеарности.

1. Коэффициент детерминации R2 достаточно высок, но некоторые из коэффициентов уравнения множественной линейной регрессии статистически незначимы (имеют низкие t-статистики).

2. Высокая корреляция в уравнении регрессии с двумя объясняющими переменными. Если объясняющих переменных больше двух целесообразнее использовать частные коэффициенты корреляции.

3. Сильная регрессия между объясняющими переменными. Какая-либо из объясняющих переменных является комбинацией других объясняющих переменных (линейной или близкой к линейной).