Обнаружение автокорреляции в регрессионных моделях.

Автокорреляция — корреляционная зависимость между текущими уровнями некоторой переменной и уровнями этой же переменной, сдвинутыми на несколько периодов времени назад. Автокорреляция случайной составляющей ε — корреляционная зависимость текущих 𝜀𝑖 и предыдущих и 𝜀𝑖−𝐿 значений случайной составляющей. Величина L называется запаздыванием, сдвигом во времени или лагом. Лаг определяет порядок автокорреляции. Автокорреляция случайной составляющей нарушает 3-ю предпосылку нормальной линейной модели регрессии: случайные отклонения 𝜀𝑖 и 𝜀𝑗 (i ≠ j) не коррелируют (отсутствует автокорреляция): 𝑀 𝜀𝑖 , 𝜀𝑗 = 0, 𝑖 ≠ 𝑗 .Обычно автокорреляция встречается при использовании данных временных рядов. Допустим, что случайная составляющая обусловлена только невключением в модель объясняющих переменных. Тогда, если значение 𝜀𝑖 в i-м наблюдении должно быть независимым от его значения в предыдущем (i - L)-oм наблюдении 𝜀𝑖−𝐿 , то и значение любой факторной переменной, «скрытой» в ε, должно быть некоррелированным с ее значением в предыдущем наблюдении. Среди основных причин, вызывающих появление автокорреляции, можно выделить ошибки спецификации, инерцию в изменении экономических показателей, эффект паутины, сглаживание данных. Автокорреляция может быть как положительной, так и отрицательной. Положительная автокорреляция означает постоянное в одном направлении действие неучтенных факторов на результат. Отрицательная автокорреляция означает разнонаправленное действие неучтенных в модели факторов на результат, что приводит к отрицательной корреляции между последовательными значениями случайной составляющей. Выводы по t- и F-статистикам, определяющим значимость коэффициентов регрессии уравнения и коэффициента детерминации R 2 , возможно, будут неверными. Вследствие этого ухудшаются прогнозные качества модели.

50.Доверительные интервалы для зависимой переменной в уравнении парной линейной регрессии. (15 баллов)

Базовой предпосылкой МНК является предположение о нормальном распределении отклонений 𝜀𝑖 с нулевым математическим ожиданием и постоянной дисперсией 𝜎 2 , которое является теоретически и практически обоснованным: 𝜀𝑖~𝑁(0; 𝜎 2 ). Согласно модельному уравнению линейной парной регрессии 𝑦𝑖 = 𝛽0 + 𝛽1 𝑥𝑖 + 𝜀𝑖 , коэффициенты 𝑏0 и 𝑏1 через 𝑦𝑖 являются линейными комбинациями 𝜀𝑖 . Следовательно, 𝑏0 и 𝑏1 также имеют нормальное распределение: 𝑏1~𝑁(𝛽1 ; 𝑆𝑏1 2 ), 𝑏0~𝑁(𝛽0 ; 𝑆𝑏0 2 ). Тогда случайные величины 𝑡𝑏1 = 𝑏1−𝛽1 𝑆𝑏1 и 𝑡𝑏0 = 𝑏0−𝛽0 𝑆𝑏0 (2.29) имеют распределение Стьюдента с числом степеней свободы 𝜈 = 𝑛 − 2. По заданной доверительной вероятности γ можно найти интервал: −𝑡кр < 𝑡 < 𝑡кр или 𝑡 < 𝑡кр внутри которого находятся значения 𝑡 с вероятностью γ: 𝑃(|𝑡| < 𝑡кр) = 𝛾. Критическое значение 𝑡кр при доверительной вероятности 𝛾 = 1 − 𝛼 находятся по таблицам двусторонних квантилей распределения Стьюдента 𝑡кр = 𝑡𝛼;𝑛−2 . Таким образом: 𝑃(−𝑡кр < 𝑏1−𝛽1 𝑆𝑏1 < 𝑡кр) = 𝛾, 𝑃(−𝑡кр < 𝑏0−𝛽0 𝑆𝑏0 < 𝑡кр) = 𝛾 (2.31) После преобразований получим: 𝑃(𝑏1 − 𝑡кр𝑆𝑏1 < 𝛽1 < 𝑏1 + 𝑡кр𝑆𝑏1 ) = 𝛾, 𝑃(𝑏0 − 𝑡кр𝑆𝑏0 < 𝛽0 < 𝑏0 + 𝑡кр𝑆𝑏0 ) = 𝛾. Доверительные интервалы для коэффициентов парной линейной регрессии с доверительной вероятностью 𝛾 = 1 − 𝛼 имеют вид: 𝑏1 − 𝑡кр𝑆𝑏1 < 𝛽1 < 𝑏1 + 𝑡кр𝑆𝑏1 , 𝑏0 − 𝑡кр𝑆𝑏0 < 𝛽0 < 𝑏0 + 𝑡кр𝑆𝑏0 .

51. Методы устранения автокорреляции в регрессионных моделях. (15 баллов)

Чаще всего автокорреляция вызывается неправильной спецификацией модели, поэтому необходимо прежде всего скорректировать саму модель. Если все разумные процедуры изменения спецификации модели исчерпаны, а автокорреляция имеет место, то можно предположить, что она обусловлена какими-то внутренними свойствами ряда остатков {еt}. В этом случае можно воспользоваться авторегрессионным преобразованием. Обычно наиболее целесообразным и простым преобразованием является авторегрессионная схема первого порядка AR(1). Рассмотрим модель парной линейной регрессии 𝑌 = 𝛽0 + 𝛽1𝑋 + 𝜀. (4.5) Тогда наблюдениям t; и (t - 1) соответствуют формулы: 𝑦𝑡 = 𝛽0 + 𝛽1 𝑥𝑡 + 𝑒𝑡 , (4.6) и 𝑦𝑡−1 = 𝛽0 + 𝛽1 𝑥𝑡−1 + 𝑒𝑡−1 . (4.7) Пусть случайные отклонения подвержены воздействию авторегрессии первого порядка 𝜀𝑡 = 𝜌𝜀𝑡−1 + 𝑣𝑡 , где 𝑣𝑡 -случайные отклонения, удовлетворяющие всем предпосылкам МНК, а коэффициент 𝜌 известен. Вычтем из (4.6) соотношение (4.7), умноженное на 𝜌: 𝑦𝑡 ∗ = 𝛽0 ∗ + 𝛽1 𝑥𝑡 ∗ + 𝑣𝑡 , (4.8) где: 𝑦𝑡 ∗ = 𝑦𝑡 − 𝜌𝑦𝑡−1 ; 𝑥𝑡 ∗ = 𝑥𝑡 − 𝜌𝑥𝑡−1 ; 𝛽0 ∗ = 𝛽0 ∗ (1 − 𝜌). Так как по предположению коэффициент 𝜌 известен, то очевидно, 𝑦𝑡 ∗ , 𝑥𝑡 ∗ , 𝛽0 ∗ , 𝑣𝑡 вычисляются достаточно просто. В силу того, что случайные отклонения 𝑣𝑡 удовлетворяют предпосылкам МНК, оценки 𝛽0 ∗ и 𝛽1 будут обладать свойствами наилучших линейных несмещенных оценок. На практике значение коэффициента 𝜌 обычно неизвестно и его необходимо оценивать.

52. Проверка общего качества уравнения регрессии. (15 баллов)

Для такой проверки используется коэффициент детерминации R 2 , который в общем случае рассчитывается по формуле: 𝑅 2 = (𝑦 𝑖−𝑦 ) 𝑛 2 𝑖=1 (𝑦𝑖−𝑦 ) 𝑛 2 𝑖=1 . (5.15) Величина R 2 является мерой объясняющего качества уравнения регрессии по сравнению с горизонтальной линией y y = . 𝑄𝑦 = (𝑦𝑖 − 𝑦 ) 𝑛 2 𝑖=1 - полная сумма квадратов отклонений – мера разброса (рассеивания) наблюдаемых значений объясняемой переменной y относительно ее среднего значения y . 𝑄𝑅 = (𝑦 𝑖 − 𝑦 ) 𝑛 2 𝑖=1 - объясненная сумма квадратов отклонений – мера разброса, объясненного уравнением регрессии. 𝑄𝑒 = 𝑒𝑖 2 = 𝑛 𝑖=1 (𝑦𝑖 − 𝑦 𝑖 ) 𝑛 2 𝑖=1 - остаточная (необъясненная) сумма квадратов отклонений – мера разброса точек вокруг линии регрессии. Как было показано ранее (Лекция 1): 𝑄𝑦 = 𝑄𝑅 + 𝑄𝑒 (5.16) Следовательно: 𝑅 2 = 𝑄𝑅 𝑄𝑦 = 1 − 𝑄𝑒 𝑄𝑦 . (5.17) Справедливо соотношение:0 ≤ 𝑅 2 ≤ 1. Чем ближе R 2 к 1, тем больше уравнение регрессии объясняет поведение Y. В отличии от случая парной регрессии, для множественной регрессии R 2 является неубывающей функцией числа объясняющих переменных. Каждая следующая добавленная объясняющая переменная может лишь дополнить информацию, объясняющую поведение Y, и увеличить R 2 . Для множественной регрессии используется скорректированный (исправленный) коэффициент детерминации для получения несмещенных оценок: 𝑅 2 = 1 − 𝑄𝑒 /(𝑛−𝑚−1) 𝑄𝑦 /(𝑛−1) , (5.18) где: 𝑄𝑦 /(𝑛 − 1) - несмещенная оценка общей дисперсии. Число ее степеней свободы равно (n – 1). 𝑄𝑒 /(𝑛 − 𝑚 − 1) - несмещенная оценка остаточной дисперсии. Ее число степеней свободы равно (n – m – 1). Потеря (m+1) степени свободы связана с необходимостью решения системы (m+1) линейного уравнения при определении коэффициентов эмпирического уравнения регрессии. Скорректированный (исправленный) коэффициент детерминации 𝑅 2 можно представить в виде: 𝑅 2 = 1 − (1 − 𝑅 2 ) ∙ 𝑛−1 𝑛−𝑚−1 . (5.19) Видно, что 𝑅 2 < 𝑅 2 для m > 1. С увеличением числа объясняющих переменных m скорректированный коэффициент детерминации 𝑅 2 растет медленнее, чем 𝑅 2 ; он корректируется в сторону уменьшения с ростом числа объясняющих переменных. Отметим: 1). 𝑅 2 = 𝑅 2 только при 𝑅 2 = 1 (функциональная зависимость). При полном отсутствии корреляции (𝑅 2 = 0) скорректированный коэффициент детерминации может принимать отрицательные значения. 2). 𝑅 2 увеличивается при добавлении новой объясняющей переменной только тогда, когда t - статистика для этой переменной по модулю больше единицы. Поэтому новые переменные можно добавлять в модель до тех пор, пока растет 𝑅 2 . 3). 𝑅 2 рассматривается лишь как один из ряда показателей, который нужно анализировать, чтобы уточнить построенную модель регрессии.

53. Фиктивные переменные в уравнении регрессии. (15 баллов)

Термин “фиктивные переменные” используется как противоположность “значащим” переменным, показывающим уровень количественного показателя, принимающего значения из непрерывного интервала. Как правило, фиктивная переменная — это индикаторная переменная, отражающая качественную характеристику. Чаще всего применяются бинарные фиктивные переменные, принимающие два значения, 0 и 1, в зависимости от определенного условия. Например, в результате опроса группы людей 1 может означать, что опрашиваемый — мужчина, а 0 — женщина. К фиктивным переменным иногда относят регрессор, состоящий из одних единиц, а также временной тренд. Фиктивные переменные, будучи экзогенными, не создают каких-либо трудностей при применении МНК. Фиктивные переменные являются эффективным инструментом построения регрессионных моделей и проверки гипотез. В общем случае, когда качественный признак имеет более двух значений, вводится несколько бинарных переменных. При использовании нескольких бинарных переменных необходимо исключить линейную зависимость между переменными, так как в противном случае, при оценке параметров, это приведет к совершенной мультиколлинеарности. Поэтому применяется следующее правило: если качественная переменная имеет k альтернативных значений, то при моделировании используются только k -1 фиктивная переменная. В регрессионных моделях применяются фиктивные переменные двух типов: переменные сдвига и переменные наклона.

54. Множественная линейная регрессия. Определение параметров уравнения регрессии. (15 баллов)

Обычно на любой экономический показатель влияет не один, а несколько факторов. Например, спрос на некоторый товар определяется не только его ценой, но и ценами на замещающие и дополняющие товары, доходом потребителей и другими факторами. В этом случае вместо функции парной регрессии 𝑀(𝑌|𝑋 = 𝑥) = 𝑓(𝑥) рассматривается функция множественной регрессии: 𝑀(𝑌|𝑋1 = 𝑥1 ; 𝑋2 = 𝑥2 ; … ; 𝑋𝑚 = 𝑥𝑚 ) = 𝑓(𝑥1 ; 𝑥2 ; … ; 𝑥𝑚 ). (5.1) 3 Теоретическая модель множественной линейной регрессии имеет вид: 𝑌 = 𝛽0 + 𝛽1𝑋1 + 𝛽2𝑋2 + ⋯ + 𝛽𝑚 𝑋𝑚 + 𝜀 (5.2) или для индивидуальных наблюдений: 𝑦𝑖 = 𝛽0 + 𝛽1 𝑥𝑖1 + 𝛽2 𝑥𝑖2 + ⋯ + 𝛽𝑚 𝑥𝑖𝑚 + 𝜀, (5.3) 𝑖 = 1, 2, … 𝑁, где N – объем генеральной совокупности. После выбора в качестве модели линейной функции множественной регрессии необходимо оценить коэффициенты регрессии. 4 Пусть имеется n наблюдений вектора объясняющих переменных 𝑋 = (𝑋1 ; 𝑋2 ; . . 𝑋𝑚 ) и зависимой переменной Y: (𝑥𝑖1 ; 𝑥𝑖2 ; … ; 𝑥𝑖𝑚 ; 𝑦𝑖 ), 𝑖 = 1, 2, … , 𝑛. (5.4) Если 𝑛 = 𝑚 + 1, то оценки коэффициентов рассчитываются единственным образом. Здесь 𝑚 – число объясняющих переменных. Если 𝑛 < 𝑚 + 1, то система будет иметь бесконечное множество решений. Если 𝑛 > 𝑚 + 1, то нельзя подобрать линейную функцию (5.2), точно удовлетворяющую всем наблюдениям, и возникает необходимость оптимизации, т.е. нахождения оценок параметров модели (5.3), при которых линейная функция дает наилучшее приближение для имеющихся наблюдений. 5 Самым распространенным методом оценки параметров модели множественной линейной регрессии является метод наименьших квадратов (МНК). Для применения МНК необходима выполнимость ряда предпосылок, которые позволят проводить анализ в рамках классической линейной модели множественной регрессии (КЛММР). Для случая множественной линейной регрессии необходимо выполнение дополнительных предпосылок.

55. Фиктивные переменные сдвига в уравнении регрессии. Пример. (15 баллов)

Рассмотрим применение фиктивных переменных для функции спроса. Предположим, что по группе лиц мужского и женского пола изучается линейная зависимость потребления кофе от цены. В общем виде для совокупности обследуемых лиц уравнение регрессии имеет вид: 𝒚 = 𝒃𝟎 + 𝒃𝟏 ∗ 𝒙 + 𝜺, (8.1) где y - количество потребляемого кофе; x - цена. Аналогичные уравнения могут быть найдены отдельно для лиц мужского пола: 𝑦1 = 𝑏0 + 𝑏11 ∗ 𝑥1 + 𝜀1 и женского - 𝑦2 = 𝑏0 + 𝑏12 ∗ 𝑥2 + 𝜀2 . Различия в потреблении кофе проявятся в различии средних у 1 и 𝑦 2. 42 Вместе с тем сила влияния x на y может быть одинаковой, т.е. 𝑏1 ≈ 𝑏11 ≈ 𝑏12. В этом случае возможно построение общего уравнения регрессии с включением в него фактора «пол» в виде фиктивной переменной. Объединяя уравнения у1 и у2 и, вводя фиктивные переменные, можно прийти к следующему выражению: 𝑦 = 𝑎1 ∙ 𝑧1 + 𝑎2 ∙ 𝑧2 + 𝑏1 ∙ 𝑥 + 𝜀, (8.2) где 𝑧1 и 𝑧2 - фиктивные переменные, принимающие значения: 𝑧1 = 1 – мужской пол, 0 − женский пол; 𝑧2 = 0 – мужской пол, 1 − женский пол. (8.3) 43 В общем уравнении регрессии зависимая переменная у рассматривается не только как функция цены 𝑥, но и пола (𝑧1 ; 𝑧2 ). Переменная z рассматривается как двоичная переменная, принимающая всего два значения: 1 и 0. При этом когда 𝑧1 = 1, то 𝑧2 = 0, и наоборот. Для лиц мужского пола, когда 𝑧1 = 1 и 𝑧2 = 0, объединенное уравнение регрессии составит: у = а1 + 𝑏1 ∙ 𝑥, а для лиц женского пола, когда 𝑧1 = 0 и 𝑧2 = 1 уравнение регрессии у = а2 + 𝑏1 ∙ 𝑥. Иными словами, различия в потреблении кофе для лиц мужского и женского пола вызваны различиями свободных членов уравнения регрессии: 𝑎1 ≠ 𝑎2 . Параметр 𝑏1 является общим для всей совокупности лиц, как для мужчин, так и для женщин. 44 Однако при введении двух фиктивных переменных 𝑧1 и 𝑧2 в модель у = а1∙ 𝑧1 + а2∙ 𝑧2 + 𝑏1 ∙ 𝑥 +𝜀 (8.4) применение МНК для оценивания параметров а1 и а2 приведет к вырожденной матрице исходных данных, и невозможности получения оценок коэффициентов уравнения регрессии. Объясняется это тем, что при использовании МНК в данном уравнении появляется свободный член, т.е. уравнение примет вид у = 𝑏0 + а1∙ 𝑧1 + а2∙ 𝑧2 + 𝑏1 ∙ 𝑥 +𝜀 (8.5) 45 Предполагая при параметре 𝑏0 независимую переменную, равную 1, имеем следующую матрицу исходных данных (объясняющих переменных): 1 1 1 1 0 𝑥1 0 𝑥2 1 0 1 𝑥3 1 ⋯ 1 1 ⋯ 0 0 𝑥4 … … 1 𝑥𝑛 В рассматриваемой матрице существует линейная зависимость между первым, вторым и третьим столбцами: первый равен сумме второго и третьего столбцов. Поэтому матрица исходных факторов вырождена. 46 Выходом из создавшегося затруднения может явиться переход к уравнениям y = 𝑏0 + 𝑏1 𝑥 + 𝑏2 𝑧1 + 𝜀, или y = 𝑏0 + 𝑏1 𝑥 + 𝑏2 𝑧2 + 𝜀, т.е. каждое уравнение включает только одну фиктивную переменную 𝒛𝟏 или 𝒛𝟐. 47 Предположим, что определено уравнение 𝑦 = 𝑏0 + 𝑏1 ∙ 𝑥 + 𝑏2 ∙ 𝑧 + 𝜀, где z принимает значения 1 для мужчин и 0 для женщин. Теоретические значения размера потребления кофе для мужчин будут получены из уравнения 𝑦 = 𝑏0 + 𝑏1 ∙ 𝑥 + 𝑏2 . Для женщин соответствующие значения получим из уравнения 𝑦 = 𝑏0 + 𝑏1 ∙ 𝑥. Сопоставляя эти результаты, видим, что различия в уровне потребления мужчин и женщин состоят в различии свободных членов данных уравнений: 𝑏0 - для женщин и 𝑏0 + 𝑏2 - для мужчин. 48 Теперь качественный фактор принимает только два состояния, которым соответствуют значения 1 и 0. Если же число градаций качественного признака-фактора превышает два, то в модель вводится несколько фиктивных переменных, число которых должно быть меньше числа качественных градаций. Вывод: Только при соблюдении этого положения матрица исходных фиктивных переменных не будет линейно зависима и возможна оценка параметров модели.

Пример 8.1. Проанализируем зависимость цены двухкомнатной квартиры от ее полезной площади. При этом в модель могут быть введены фиктивные переменные, отражающие тип дома: «хрущевка», панельный, кирпичный. При использовании трех категорий домов вводятся две фиктивные переменные: z1 и z2. Пусть переменная z1 принимает значение 1 для панельного дома и 0 для всех остальных типов домов; переменная z2 принимает значение 1 для кирпичных домов и 0 для остальных; тогда переменные z1 и z2 принимают значения 0 для домов типа «хрущевки». 50 Предположим, что уравнение регрессии с фиктивными переменными имеет вид: у = 320 + 500x+2200z1 +1600z2. Частные уравнения регрессии для отдельных типов домов, свидетельствуя о наиболее высоких ценах квартир в панельных домах, будут иметь следующий вид: «хрущевки» - у = 320 + 500x; панельные - у = 2520 + 500x; кирпичные - у = 1920 + 500x. Параметры при фиктивных переменных z1 и z2 представляют собой разность между средним уровнем результативного признака для соответствующей группы и базовой группы. В рассматриваемом примере за базу сравнения цены взяты дома «хрущевки», для которых z1 = z2 = 0. 51 Параметр при z1, равный 2200, означает, что при одной и той же полезной площади квартиры цена ее в панельных домах в среднем на 2200 ден.ед. выше, чем в «хрущевках». Соответственно параметр при z2 показывает, что в кирпичных домах цена выше в среднем на 1600 ден.ед. при неизменной величине полезной площади по сравнению с указанным типом домов.

56. Расчет коэффициентов уравнения множественной линейной регрессии. Система нормальных уравнений. (15 баллов)

Истинные значения коэффициентов bj по выборке получить невозможно. Вместо теоретического уравнения оценивается эмпирическое уравнение регрессии для индивидуальных наблюдений: 𝑦𝑖 = 𝑏0 + 𝑏1 𝑥𝑖1 + 𝑏2 𝑥𝑖2 + ⋯ + 𝑏𝑚 𝑥𝑖𝑚 + 𝑒𝑖 . (5.5) Здесь 𝑏0 , 𝑏1 , 𝑏2 , … , 𝑏𝑚 - эмпирические коэффициенты регрессии (оценки теоретических коэффициентов (𝛽0 , 𝛽1 , 𝛽2 , … , 𝛽𝑚 ). 𝑒𝑖 - остатки (оценки отклонений 𝜀𝑖 ). Согласно МНК, для нахождения оценок 𝑏0 ; 𝑏1 ; … ; 𝑏𝑚 минимизируется сумма квадратов остатков: 𝑄𝑒 = 𝑒𝑖 𝑛 2 𝑖=1 = 𝑦𝑖 − 𝑏0 + 𝑏𝑗 𝑥𝑖𝑗 𝑚 𝑗=1 2 𝑛 𝑖=1 . (5.6) Данная функция является квадратичной относительно неизвестных коэффициентов. Она ограничена снизу, следовательно, имеет минимум. Необходимым условием минимума Qe является равенство нулю частных производных 𝜕𝑄𝑒 𝜕𝑏𝑗 = 0, 𝑗 = 0, 1, 2, … , 𝑚. (5.7) Приравнивая их к нулю, получаем систему m + 1 линейных уравнений с m + 1 неизвестными: 𝑦𝑖 − 𝑏0 + 𝑏𝑗 𝑥𝑖𝑗 𝑚 𝑗=1 𝑛 𝑖=1 = 0 𝑦𝑖 − 𝑏0 + 𝑏𝑗 𝑥𝑖𝑗 𝑚 𝑗=1 𝑥𝑖𝑗 𝑛 𝑖=1 = 0 𝑗 = 1, 2, … , 𝑚. (5.8) Эта система называется системой нормальных уравнений. Представим данные наблюдений и соответствующие коэффициенты в матричной форме: 𝑋 = 1 𝑥11 𝑥12 1 𝑥21 𝑥22 1 𝑥31 𝑥32 ⋯ ⋯ ⋯ 𝑥1𝑚 𝑥2𝑚 𝑥3𝑚 ⋯ ⋯ ⋯ ⋯ ⋯ 1 𝑥𝑛1 𝑥𝑛2 ⋯ 𝑥𝑛𝑚 . (5.9) Х – матрица объясняющих переменных размера n × (m+1), в которой xij – значение переменной Xj в i-м наблюдении; 1 соответствует переменной при b0. 𝑌 = 𝑦1 𝑦2 … 𝑦𝑛 ; 𝐵 = 𝑏0 𝑏1 … 𝑏𝑚 ; 𝑒 = 𝑒1 𝑒2 … 𝑒𝑛 . (5.10) Здесь Y – матрица размера n × 1 наблюдаемых значений зависимой переменной Y; B - матрица размера (m+1) × 1 оценок коэффициентов модели; е – матрица остатков размера n × 1 (отклонений наблюдаемых значений 𝑦𝑖 от расчетных значений 𝑦 𝑖 = 𝑏0 + 𝑏𝑗 𝑥𝑖𝑗 𝑚 𝑗=1 , получаемых по линии регрессии). Уравнение регрессии в матричной форме: 𝑌 = 𝑋𝐵 + 𝑒. (5.11) 𝑒 = 𝑌 − 𝑋𝐵. (5.12) Функция, которая минимизируется 𝑄𝑒 = 𝑒𝑖 𝑛 2 𝑖=1 . (5.13). Общая формула вычисления вектора B оценок коэффициентов модели множественной линейной регрессии: 𝐵 = (𝑋 𝑇 𝑋) −1 𝑋 𝑇 𝑌, (5.14) здесь X T – транспонированная матрица 𝑋, 𝑋 𝑇 ∙ 𝑋 - произведение матриц, (𝑋 𝑇 ∙ 𝑋) −1 матрица обратная к матрице 𝑋 𝑇 ∙ 𝑋. Вывод: Полученные общие соотношения (5.14) справедливы для уравнений регрессии с произвольным количеством m объясняющих переменных.

Фиктивные переменные наклона в уравнении регрессии. Пример

Любые примеры обеспечивали интерпретацию сдвига графиков (вверх, вниз) при изменении качественного признака. При этом предполагалось, что наклон графика не зависит от качественного признака, что не всегда верно. В связи с этим введем фиктивную переменную для коэффициента наклона, называемый иногда фиктивной переменной взаимодействия. В любом ранее примере с рождением первенца/не первенца уравнение регрессии имело вид: D=0- если первенец; D=1-если не первенец

Введем дополнительную фиктивную переменную для коэффициента наклона графика:

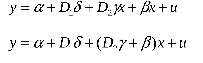
D1=0,D2=0, если первенец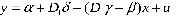

D1=0,D2=0, если первенец

D1=1,D2=1, если не первенец

Доугерти провел исслед-ие и получил: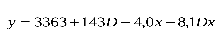

Если первенец=(3363-4х)гр. Если матери курят, (график)

Если не перв.=(3410-12х)гр. то вес меньше

58. Какие существуют способы построения систем линейных одновременных уровнений? Чем они отличаются друг от друга?

Наибольшее распространение в эконометрических исследованиях получила система одновременных (взаимозависимых) уравнений. В ней одни и те же зависимые (исследуемые) переменные в одних уравнениях входят в левую часть, а других – в правую часть системы. Даже в простейшем случае системы одновременных линейных уравнений (eё также называют структурной формой модели – СФМ) :

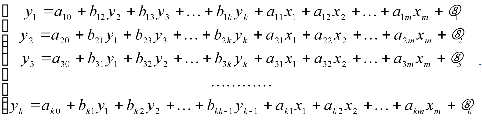
определение параметров модели сталкивается с большими трудностями и не всегда возможно в принципе. Для нахождения параметров модели исходная система одновременных линейных уравнений сводится к приведённой форме модели (ПФМ), которая имеет вид системы независимых переменных:

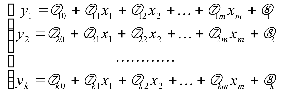
Такое сведение всегда возможно произвести с помощью алгебраических преобразований исходной системы уравнений. Параметры приведённой системы δij можно находить с помощью МНК. Основная трудность заключается в том, что не всегда возможно по коэффициентам приведённой системы восстановить коэффициенты исходной системы уравнений, то есть осуществить обратный переход (подобно тому, как мы это делали, сводя нелинейное уравнение к линейному, находя параметры линейной модели, а затем производя обратный пересчёт параметров нелинейной модели).

Проблема перехода от приведённой формы (ПФМ) системы уравнений к исходной СФМ называется проблемой идентификации. Различаются идентифицируемые, неидентифицируемые и сверхидентифицируемые модели.

Модель идентифицируема, если все коэффициенты исходной модели определяются однозначно, единственным образом по коэффициентам приведённой модели. Это возможно когда число параметров исходной модели равно числу параметров приведённой формы (здесь и далее не учитывается число свободных коэффициентов в уравнениях). Процедура нахождения коэффициентов идентифицируемой модели носит название косвенного метода наименьших квадратов (КМНК) и содержит следующие этапы:

а) исходная модель преобразуется в приведённую форму модели;

б) для каждого уравнения приведённой формы модели применяется обычный МНК;

в) коэффициенты приведённой модели трансформируются в коэффициенты исходной модели.

2. Модель неидентифицируема, если число параметров приведённой системы меньше чем, число параметров исходной модели, и в результате коэффициенты исходной модели не могут быть оценены через коэффициенты приведённой формы.

3. Модель сверхидентифицируема, если число приведённых коэффициентов больше числа коэффициентов в исходной модели. В этом случае на основе коэффициентов приведённой формы можно получить два и более значений одного коэффициента исходной модели. Сверхидентифицируемая модель в отличие от неидентифицируемой модели практически разрешима, но требует специальных методов исчисления параметров. Наиболее распространённым является двух шаговый метод наименьших квадратов (ДНМК). Основная идея ДНМК – на основе приведённой формы модели получить для сверхидентифицируемого уравнения (имеются критерии для определения идентифицируемости каждого уравнения исходной системы) теоретические значения исследуемых переменных, содержащегося в правой части уравнения. Далее, подставив эти значения вместо фактических значений (результатов наблюдений), применяется МНК к сверхидентифицируемому уравнению исходной системы.