Методы устранения автокорреляции.

Чаще всего автокорреляция вызывается неправильной спецификацией модели, поэтому необходимо прежде всего скорректировать саму модель. Если все разумные процедуры изменения спецификации модели исчерпаны, а автокорреляция имеет место, то можно предположить, что она обусловлена какими-то внутренними свойствами ряда остатков {еt}. В этом случае можно воспользоваться авторегрессионным преобразованием. Обычно наиболее целесообразным и простым преобразованием является авторегрессионная схема первого порядка AR(1). Рассмотрим модель парной линейной регрессии 𝑌 = 𝛽0 + 𝛽1𝑋 + 𝜀. (4.5) Тогда наблюдениям t; и (t - 1) соответствуют формулы: 𝑦𝑡 = 𝛽0 + 𝛽1 𝑥𝑡 + 𝑒𝑡 , (4.6) и 𝑦𝑡−1 = 𝛽0 + 𝛽1 𝑥𝑡−1 + 𝑒𝑡−1 . (4.7) Пусть случайные отклонения подвержены воздействию авторегрессии первого порядка 𝜀𝑡 = 𝜌𝜀𝑡−1 + 𝑣𝑡 , где 𝑣𝑡 -случайные отклонения, удовлетворяющие всем предпосылкам МНК, а коэффициент 𝜌 известен. Вычтем из (4.6) соотношение (4.7), умноженное на 𝜌: 𝑦𝑡 ∗ = 𝛽0 ∗ + 𝛽1 𝑥𝑡 ∗ + 𝑣𝑡 , (4.8) где: 𝑦𝑡 ∗ = 𝑦𝑡 − 𝜌𝑦𝑡−1 ; 𝑥𝑡 ∗ = 𝑥𝑡 − 𝜌𝑥𝑡−1 ; 𝛽0 ∗ = 𝛽0 ∗ (1 − 𝜌). Так как по предположению коэффициент 𝜌 известен, то очевидно, 𝑦𝑡 ∗ , 𝑥𝑡 ∗ , 𝛽0 ∗ , 𝑣𝑡 вычисляются достаточно просто. В силу того, что случайные отклонения 𝑣𝑡 удовлетворяют предпосылкам МНК, оценки 𝛽0 ∗ и 𝛽1 будут обладать свойствами наилучших линейных несмещенных оценок. На практике значение коэффициента 𝜌 обычно неизвестно и его необходимо оценивать.

Фиктивные переменные в уравнении регрессии.

Термин “фиктивные переменные” используется как противоположность “значащим” переменным, показывающим уровень количественного показателя, принимающего значения из непрерывного интервала. Как правило, фиктивная переменная — это индикаторная переменная, отражающая качественную характеристику. Чаще всего применяются бинарные фиктивные переменные, принимающие два значения, 0 и 1, в зависимости от определенного условия. Например, в результате опроса группы людей 1 может означать, что опрашиваемый — мужчина, а 0 — женщина. К фиктивным переменным иногда относят регрессор, состоящий из одних единиц, а также временной тренд. Фиктивные переменные, будучи экзогенными, не создают каких-либо трудностей при применении МНК. Фиктивные переменные являются эффективным инструментом построения регрессионных моделей и проверки гипотез. В общем случае, когда качественный признак имеет более двух значений, вводится несколько бинарных переменных. При использовании нескольких бинарных переменных необходимо исключить линейную зависимость между переменными, так как в противном случае, при оценке параметров, это приведет к совершенной мультиколлинеарности. Поэтому применяется следующее правило: если качественная переменная имеет k альтернативных значений, то при моделировании используются только k -1 фиктивная переменная. В регрессионных моделях применяются фиктивные переменные двух типов: переменные сдвига и переменные наклона.

Фиктивные переменные сдвига. Пример.

Фиктивная переменная – это качественная переменная, принимающая значения 0 и 1, включаемая в эконометрическую модель для учёта влияния качественных признаков и событий на объясняемую переменную. При этом фиктивные переменные позволяют учесть влияние не только качественных признаков, принимающих два значения, но и несколько возможных. В этом случае добавляются несколько фиктивных переменных.

Фиктивная переменная сдвига – это фиктивная переменная, которая меняет точку пересечения линии регрессии с осью ординат в случае применения качественной переменной.

К примеру, если рассматривается модель затрат на обучение в зависимости от количества учащихся и типа школы: общеобразовательной и специализированной.

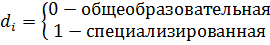
В таком случае спецификационную модель можно записать как: y_i=b₀+b₁x_i+b₂d_i+e_i, где x – непрерывная переменная (количество учащихся), а d – фиктивная (тип школы). В таком случае у нас получится уравнение регрессии, из которого получается две отдельные модели (путем присвоения переменной d значений 1 и 0):

y_i=b₀+b₁x_i+e_i – для обычных школ

y_i=(b₀+b₂)+b₁x_i+e_i – для специализированных школ.

Таким образом, в зависимости от типа школы график моделей сместиться вверх или вниз относительно оси ординат.

Фиктивные переменные наклона. Пример.

Фиктивная переменная – это качественная переменная, принимающая значения 0 и 1, включаемая в эконометрическую модель для учёта влияния качественных признаков и событий на объясняемую переменную. При этом фиктивные переменные позволяют учесть влияние не только качественных признаков, принимающих два значения, но и несколько возможных. В этом случае добавляются несколько фиктивных переменных.

Фиктивная переменная наклона – это фиктивная переменная, которая изменяет наклон линии регрессии в случае использования качественной переменной. Фиктивные переменные сдвига оказываются полезными при моделировании процессов, в которых при достижении некоторого определенного значения количественной переменной (например, времени) изменяется угол наклона прямой.

К примеру, приобретение дополнительного электроприбора изменяет интенсивность потребления электроэнергии, но не скачкообразно, а непрерыво. Предположим, что электроприбор был приобретен в третий год измерений, тогда необходимо ввести фиктивную переменную d и перекрестную (фиктивную наклона) q=d*t.

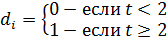
Тогда спецификационную модель можно записать в виде: y_i=b₀+b₁t_i+b₂d_i+b₃q+e_i. Соответственно, график такой модели будет выглядеть следующим образом: дорисовать график, где прямая от 0 до 2 идет под углом вверх, а с 2 и дальше под более крутым углом вверх.