Схемы и характеристики нерекурсивных фильтров с линейной ФЧХ

Актуальной задачей является синтез ЦФ с линейной ФЧХ. Такие фильтры позволяют передавать сигналы без искажения их формы.

Расчет нерекурсивных цифровых фильтров с линейной фазочастотной характеристикой является более сложной задачей.

Линейность ФЧХ нерекурсивных фильтров обеспечивается при выполнении единственного условия – симметрии или антисимметрии его импульсной характеристики:

, (3.1)

где - полное число отсчетов импульсной характеристики, включая нулевой.

Нерекурсивные цифровые фильтры, имеющие линейную ФЧХ, различаются по своим показателям в зависимости от того, являются ли их импульсные характеристики симметричными или антисимметричными, а также от четности или нечетности числа отсчетов. Соответственно, существуют четыре типа нерекурсивных фильтров с линейными ФЧХ.

Симметричные фильтры с четным числом отсчетов N

Симметрия импульсной характеристики таких фильтров определяется выражением:

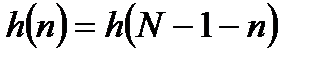. (3.2)

Осью симметрии в соответствии с рисунком является вертикальная прямая, пересекающая ось абсцисс в точке : рисунок 3.1.

Передаточная характеристика такого фильтра с учетом свойства симметрии описывается выражением:

. (3.3)

После преобразований можно получить выражение для комплексного коэффициента передачи фильтра с учетом замены :

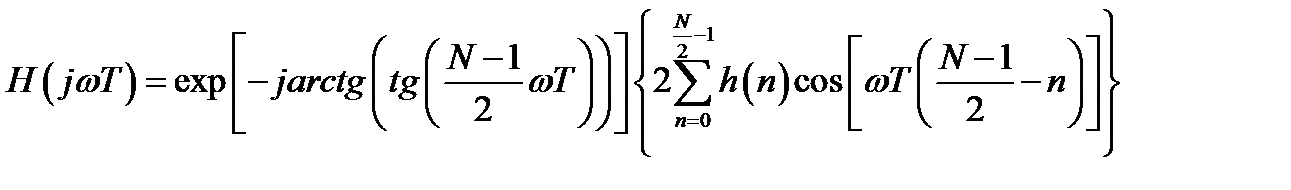. (3.3)

Соответственно, вещественная частотная характеристика (ЧХ) и ФЧХ фильтра имеют вид:

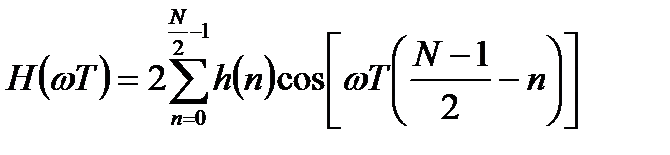; (3.4)

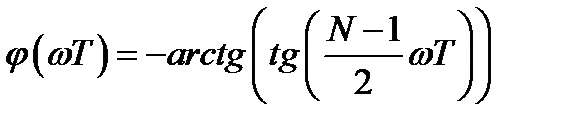. (3.5)

Рисунок 3.1 – характеристики рекурсивного фильтра типа 1

ЧХ является четной функцией аргумента 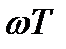. На частоте, соответствующей частоте Найквиста 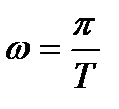, ЧХ всегда равна нулю.

ФЧХ является линейно-разрывной функцией. ФЧХ антисимметрична относительно частоты Найквиста:

. (3.6)

Возможно реализовывать только ФНЧ и ПФ. Невозможно реализовывать ФВЧ и РФ.

Антисимметричные фильтры с четным числом отсчетов N

Антисимметрия импульсной характеристики таких фильтров определяется выражением:

. (3.7)

Осью симметрии в соответствии с рисунком является вертикальная прямая, пересекающая ось абсцисс в точке : рисунок 3.2.

Выражение для комплексного коэффициента передачи такого фильтра с учетом замены может быть получено в виде:

. (3.8)

Соответственно, вещественная частотная характеристика (ЧХ) и ФЧХ фильтра имеют вид:

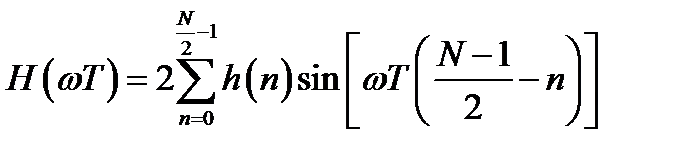; (3.9)

. (3.10)

ЧХ является нечетной функцией аргумента 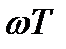. На нулевой частоте ЧХ равна нулю.

ФЧХ является линейно-разрывной функцией, антисимметрична относительно частоты Найквиста:

. (3.11)

Рисунок 3.2 – характеристики рекурсивного фильтра типа 2

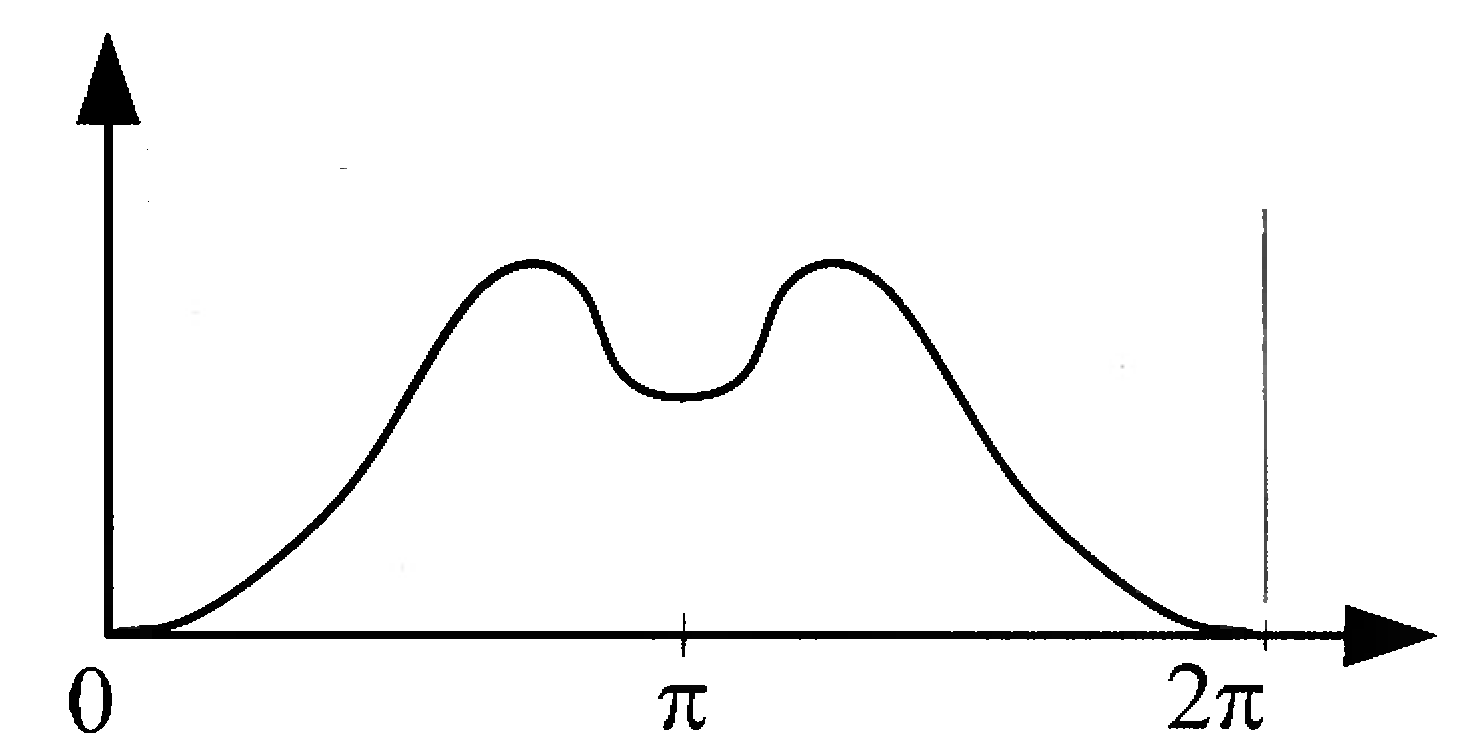
Возможна реализация фильтров ФВЧ и ПФ. Фильтр непригоден для проектирования ФНЧ. В связи со сдвигом фазы на 90° фильтр может использоваться для создания цифрового преобразователя Гильберта.Также возможно создание дифференциаторов.

Симметричные фильтры с нечетным N

Симметрия импульсной характеристики таких фильтров определяется выражением:

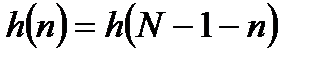. (3.12)

Осью симметрии в соответствии с рисунком является вертикальная прямая, пересекающая ось абсцисс через отсчет с номером .

Соответственно, вещественная ЧХ фильтра имеет вид:

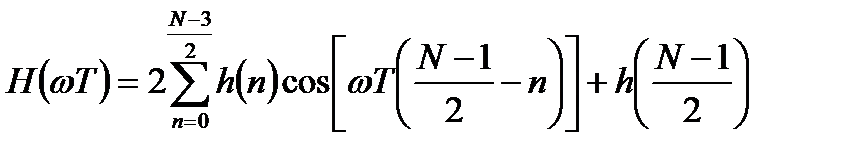. (3.13)

В соответствии с выражением (3.13) ЧХ является четной функцией частоты. Причем ЧХ не равна нулю не только при нулевом значении частоты, но и на частоте Найквиста.

Такие фильтры могут использоваться для реализации фильтров произвольной избирательности (ФНЧ, ФВЧ, ПФ, РФ и др.).

Антисимметричные фильтры с нечетным N

Симметрия импульсной характеристики таких фильтров определяется выражением:

. (3.14)

Осью симметрии в соответствии с рисунком вертикальная прямая, пересекающая ось абсцисс через отсчет с номером . Значение отсчета в центре антисимметрии равно нулю:

Соответственно, ЧХ фильтра имеет вид:

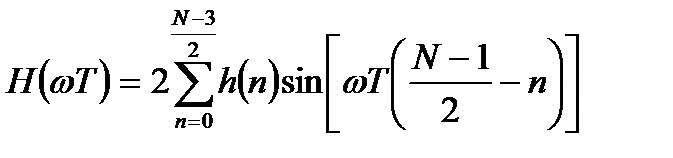. (3.15)

В соответствии с выражением (3.15) ЧХ является нечетной функцией частоты. Причем ЧХ равна нулю как при нулевом значении частоты, так и на частоте Найквиста.

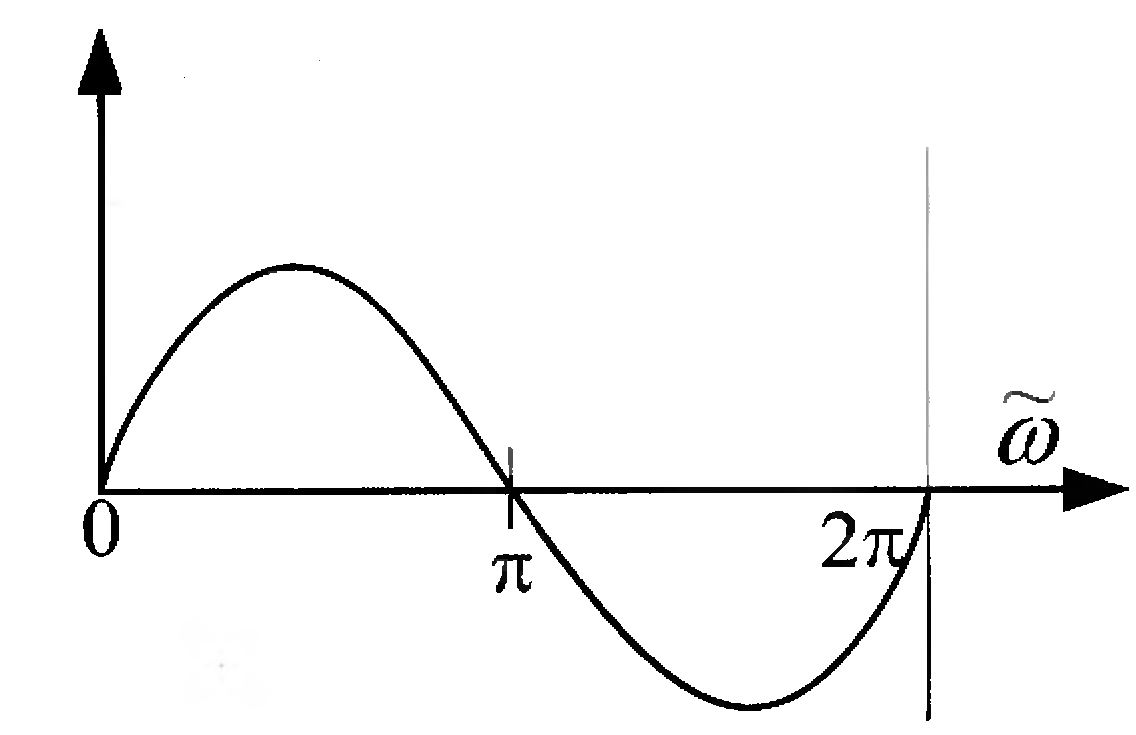
Такой фильтр целесообразно использовать только при проектировании полосового фильтра.

Литература

Маркович И.И. Цифровая обработка сигналов в системах и устройствах: монография / И.И. Маркович; Южный федеральный университет. – Ростов н/Д: Издательство Южного федерального университета, 2012. – 236 с. (стр. 108)

Гадзиковский В.И. Цифровая обработка сигналов. М.: СОЛОН-ПРЕСС, 2013. – 766 с. (с. 102)

Синтез ЦФ с линейной ФЧХ

Синтез ЦФ с линейной ФЧХ основан на представлении комплексной частотной характеристики фильтра 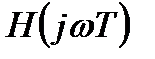в виде произведения вещественной частотной характеристики и фазового множителя :

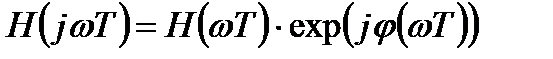. (3.16)

Вещественную частотную характеристику (ЧХ), как периодическую функцию частоты, можно представить рядом Фурье:

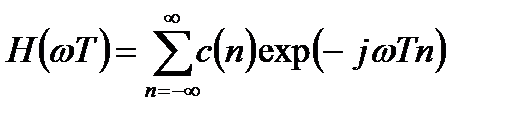, (3.17)

где .

Комплексную частотную характеристику с учетом (3.17) можно представить в виде:

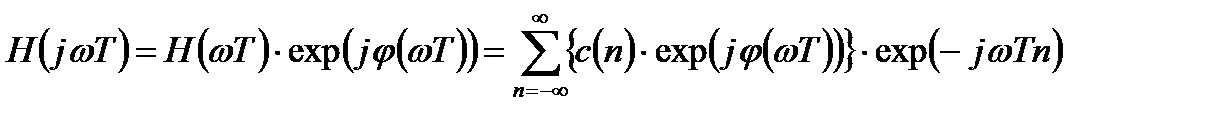. (3.18)

Учтем, что в общем случае комплексная частотная характеристика ЦФ определяется z-преобразованием от импульсной характеристики:

. (3.19)

В соответствии с выражениями (3.19) и (3.18) импульсную характеристику ЦФ можно представить через коэффициенты ряда Фурье:

. (3.20)

Ограничим импульсную характеристику конечным числом отсчетов и потребуем, чтобы ФЧХ фильтра являлась линейной:

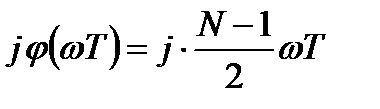. (3.21)

В этом случае импульсная характеристика ЦФ (3.20) примет вид:

. (3.22)

В операторной форме с учетом 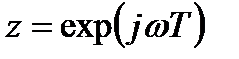выражение (3.22) запишется следующим образом:

. (3.23)

Множитель можно рассматривать как оператор сдвига, смещающий последовательность коэффициентов в сторону положительных значений 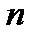на интервал :

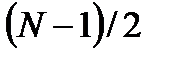. (3.24)

Таким образом, с учетом выражения (3.17) импульсную характеристику ЦФ (3.24) можно записать в виде:

. (3.25)

Для четных и нечетных функций частоты выражение (3.25) с учетом конкретизируется следующим образом:

; (3.26)

. (3.27)

С учетом действительного характера импульсной характеристики комплексный множитель в выражении (3.27) следует отнести к ФЧХ фильтра с нечетной функцией , добавив к ней постоянное угловое смещение :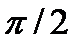

.

В этом случае множитель в выражении (3.27) можно не учитывать. Соответственно, можно сделать вывод, что ЦФ с линейной фазой и нечетной частотной характеристикой могут использоваться для синтеза цифрового преобразования Гильберта, обеспечивающего сдвиг по фазе на 90°.