Задачи контрольных работ по статике С1, С2

Филиал НИЯУ МИФИ

СТАТИКА, КИНЕМАТИКА

Индивидуальные контрольные задания

По теоретической механике

Учебно-методическое пособие

Волгодонск 2014

УДК 531

С 78

Рецензент – Синельщиков В.В. к.т.н., доцент

Составители– Пинчук Э.В., Литвинова Т.А.

Статика, кинематика: индивидуальные контрольные задания по теоретической механике: учебно-методическое пособие / Волгодонский инженерно–технический институт НИЯУ МИФИ. – Волгодонск: ВИТИ НИЯУ МИФИ, 2014. – 78 с.

Методические указания предназначены для студентов всех форм обучения машиностроительных, строительных, энергетических и других специальностей, в учебные планы которых входит дисциплина «Теоретическая механика». Они содержат контрольные задания, краткие теоретические сведения, планы решения типовых задач, примеры решения.

© ВИТИ НИЯУ МИФИ, 2014

Оглавление

Введение4

1 Содержание дисциплины5

2 Контрольные задания и методические указания к их выполнению8

2.1 Содержание заданий8

2.2 Задачи контрольных работ по статике С1, С28

2.3 Методические указания к решению задач по статике14

2.3.1 Плоская система сил14

2.3.2 Пространственная система сил19

2.4 Задачи контрольных работ по кинематике К1, К2, К3, К426

2.5 Методические указания к решению задач по кинематике34

2.5.1 Кинематика точки34

2.5.2 Вращение твёрдого тела вокруг неподвижной оси40

2.5.3 Плоское движение твёрдого тела45

2.5.4 Сложное движение точки61

3 Список литературы76

4 Приложение: образец титульного листа ИДЗ77

Введение

Теоретическая механика занимает одно из ведущих мест среди общепрофессиональных дисциплин, изучаемых в высших технических учебных заведениях. Она является теоретической базой для таких дисциплин, как «Сопротивление материалов», «Теория механизмов и машин», «Детали машин», «Строительная механика» и др.

Для успешного изучения курса теоретической механики, кроме глубокой проработки теории предмета, необходимо также приобрести твердые навыки в решении задач. С этой целью в учебных планах по дисциплине «Теоретическая механика» предусмотрено выполнение индивидуальных домашних заданий.

Целью настоящих указаний является оказание методической помощи студентам при решении задач, входящих в индивидуальные домашние задания по теоретической механике

1 Содержание дисциплины

Статика

1. Основные понятия и аксиомы статики.

Предмет статики. Основные понятия статики. Аксиомы статики. Связи и реакции связей. Принцип освобождаемости от связей. Основные виды связей.

2. Система сходящихся сил.

Геометрический способ определения равнодействующей пространственной системы сходящихся сил. Условие равновесия систем сходящихся сил в геометрической форме. Аналитический метод определения равнодействующей пространственной и плоской системы сходящихся сил. Условия равновесия пространственной и плоской системы сходящихся сил в аналитической форме. Теорема о равновесии трех непараллельных сил.

3. Момент силы относительно точки и оси.

Алгебраическая величина момента силы относительно точки. Момент силы относительно точки как вектор. Момент силы относительно оси. Связь момента силы относительно оси с вектором момента силы относительно точки на оси.

4. Теория пар сил.

Пара сил. Алгебраический момент пары сил. Момент пары как вектор (векторный момент пары). Теорема о сумме моментов сил пары относительно произвольной точки. Теоремы об эквивалентности пар сил на плоскости и о переносе пары сил в параллельную плоскость. Теорема о сложении пар сил, расположенных в пересекающихся плоскостях. Условия равновесия пар сил.

5. Приведение произвольной системы сил к данному центру.

Аналитические условия равновесия пространственной системы сил. Частные случаи. Лемма о параллельном переносе силы. Присоединенная пара сил. Главный вектор и главный момент системы сил. Аналитическое определение главного вектора и главного момента произвольной системы сил. Основная теорема статики. Аналитические условия равновесия системы сил. Теорема Вариньона о моменте равнодействующей.

6. Система сил, произвольно расположенных на плоскости.

Аналитическое определение главного вектора и главного момента плоской системы сил. Случай приведения плоской системы сил к одной паре и к равнодействующей. Случай равновесия сил. Аналитические условия равновесия. Различные формы уравнений равновесия плоской произвольной системы сил. Реакция жесткой заделки. Равновесие системы параллельных сил.

7. Трение.

Законы трения скольжения. Угол и конус трения. Область равновесия. Понятие о трении качения.

8. Центр параллельных сил и центр тяжести.

Радиус – вектор и координаты центра параллельных сил. Центр тяжести твердого тела: формулы для определения его координат. Координаты центров тяжести однородных тел (центры тяжести объема, площади и линии). Способы определения положения центра тяжести тел. Центры тяжести площади треугольника, дуги окружности, кругового сектора.

Кинематика

1. Предмет кинематики.

Пространство и время в классической механике и в теории относительности. Система отсчета. Относительность движения и покоя. Задачи кинематики.

2. Кинематика точки.

Векторный способ задания движения точки. Координатный способ задания движения точки (в прямоугольных декартовых координатах). Естественный способ задания движения точки. Естественный трехгранник. Алгебраическая величина скорости точки. Определение ускорения точки по её проекциям на оси естественного трехгранника; касательное и нормальное ускорения точки. Равномерное и равнопеременное криволинейные движения точки; законы этих движений.

3. Простейшие движения твердого тела.

Степени свободы твердого тела. Теорема о проекциях скоростей точек твердого тела.

4. Поступательное движение твердого тела. Теорема о траекториях, скоростях и ускорениях точек твердого тела при поступательном движении.

Вращение твердого тела вокруг неподвижной оси. Уравнение вращательного движения твердого тела. Угловая скорость и угловое ускорение тела. Равномерное и равнопеременное вращения твердого тела. Векторы угловой скорости и углового ускорения тела. Скорость и ускорение точек твердого тела, вращающегося вокруг неподвижной оси. Векторные выражения скорости, вращательного и центростремительного ускорений точки.

5. Плоское движение твердого тела.

Определение плоского движения твердого тела. Уравнения движения. Разложение плоского движения твердого тела на поступательное и вращательное движения. Векторная зависимость между скоростями двух точек тела при плоском движении. Мгновенный центр скоростей. Векторная зависимость между ускорениями двух точек тела при плоском движении. Мгновенный центр ускорений.

6. Сферическое движение твердого тела.

Эйлеровы углы. Уравнения движения твердого тела вокруг неподвижной точки. Мгновенная ось вращения тела. Векторы угловой скорости и углового ускорения тела. Определение скоростей и ускорений точек твердого тела, имеющего одну неподвижную точку. Понятие об аксоидах.

7. Общий случай движения твердого тела.

Разложение движения свободного твердого тела на поступательное и сферическое движения. Уравнения движения свободного твердого тела. Определение скоростей и ускорений точек свободного твердого тела.

8. Сложное движение точки.

Абсолютное, относительное и переносное движение точки. Теорема о сложении скоростей. Теорема Кориолиса о сложении ускорений. Ускорение Кориолиса.

9. Сложное движение твердого тела.

Сложение поступательных движений. Сложение мгновенных вращений твердого тела вокруг пересекающихся и параллельных осей. Пара мгновенных вращений. Сложение поступательного и вращательного движений. Винтовое движение.

2 Контрольные задания и методические указания к их выполнению

Содержание заданий

Студенты, обучающиеся по учебным планам по направлениям Электроэнергетика и электротеxника , Ядерная энергетика и теплофизика выполняют одну контрольную работу.

Она включает задачи по разделам:

статика -C1,

кинематика -K2, К4,

динамика-Д1, Д3, Д4.

К каждой задаче даётся 10 рисунков и таблица, содержащая 10 вариантов данных.

Студент во всех задачах выбирает номер рисунка по последней цифре, а номер варианта данных в таблице – по предпоследней цифре номера зачетной книжки.

Каждая задача выполняется на листах формата А4 с одной стороны. Сверху указывается номер задачи и тема, далее записываются данные из таблицы, и делается чертёж. Чертёж выполняется линейкой и циркулем, основные линии должны быть в два раза толще вспомогательных. На чертеже все углы должны соответствовать условию, размеры выполняются пропорционально данным. Слева оставляются поля – 20 мм. Решение задач необходимо сопровождать краткими пояснениями. Копированные контрольные работы не приниаются.

Плоская система сил

При решении задач на равновесие твердого тела, находящегося под действием плоской произвольной системы сил, применяются уравнения равновесия в одной из следующих форм [1]:

– суммы проекций на декартовы оси координат и сумма алгебраических моментов всех сил системы относительно произвольной точки плоскости действия сил равны нулю:

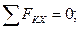
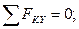
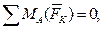
– сумма проекций на некоторую ось и сумма алгебраических моментов всех сил системы относительно двух точек плоскости, не принадлежащих прямой, перпендикулярной к оси проекций, равны нулю:

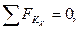
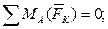
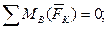
– суммы алгебраических моментов всех сил системы относительно трех точек плоскости действия сил, не принадлежащих одной прямой, равны нулю:

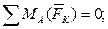
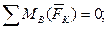
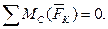
Проекция силы на ось (рис. 5) записывается по формуле:

.

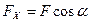Проекция будет положительна, если направлена в положительном направлении оси.

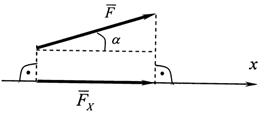
Рисунок 5 – Проекция силы

Алгебраическим моментом силы относительно данной точки называется взятое со знаком плюс или минус произведение модуля силы на ее плечо относительно этой точки (рис. 6), т.е., где h – плечо силы относительно точки А.

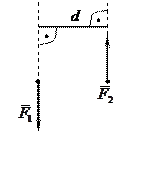
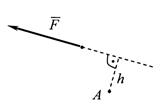
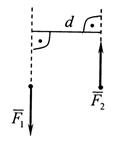
Рисунок 6 – Плечо силы Рисунок 7 – Пара сил

Момент считается положительным, если сила стремится вращать тело вокруг данной точки против часовой стрелки; если по часовой стрелке, то момент считается отрицательным.

Парой сил называется система двух равных по модулю, параллельных и противоположно направленных сил, приложенных к твердому телу (рис. 7). Алгебраический момент пары сил определяется по формуле

,

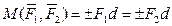где d – плечо пары сил (рис. 7).

Правило знаков для алгебраических моментов силы и пары сил одинаково.

С целью получения более простых уравнений суммы моментов сил рекомендуется составлять относительно точек, через которые проходят линии действия неизвестных сил.

В тех случаях, когда запись момента усложняется из-за трудностей при нахождении плеча силы, удобно разложить ее на составляющие, для которых плечи легко определяются, и воспользоваться теоремой Вариньона:

,

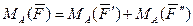где 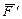, 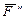– составляющие силы 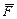, т.е. .

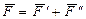План решения задач

1) Выделить на рисунке твердое тело, равновесие которого следует рассмотреть.

2) Изобразить векторы сил и моменты пар сил задаваемой нагрузки, приложенной к выделенному телу.

3) Выбрать систему координат.

4) Освободить тело от связей (опор) и заменить их соответствующими реакциями связей. Основные виды связей и их реакции приведены в любом учебнике по теоретической механике (раздел «Статика»), например в [1].

5) Для системы сил, приложенных к телу, составить уравнения равновесия.

6) Решив полученную систему уравнений, определить неизвестные реакции связей.

Пример 1. Балка АВ (рис. 8) находится в равновесии. Сила G=10 кН, момент пары сил М=8 кН*м, интенсивность распределенной нагрузки q=0,5 кН/м, Р=5 кН, ; размеры указаны в м.

Определить реакции неподвижного цилиндрического шарнира А и невесомого жесткого стержня СD.

Решение: Рассмотрим равновесие балки АВ (рис. 8).

Изобразим задаваемые силы, действующие на балку: сила 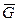, равнодействующая 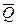равномерно-распределенной нагрузки, по величине равная 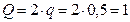кН и приложенная в середине участка действия этой нагрузки; пара сил с моментом М; сила 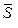натяжения троса, модуль которой равен P и которая направлена вдоль троса от балки.

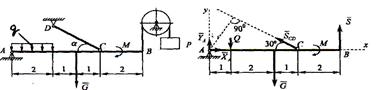
Рисунок 8 – К примеру 1 Рисунок 9 – К примеру 1

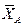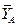Отбрасываем связи: шарнирно-неподвижную опору А и невесомый жесткий стержень CD. Действие связей заменяем их реакциями (рис. 9). Реакцию опоры А представляем двумя составляющими и . Силу реакции стержня 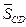направляем вдоль стержня от балки (можно ввести ее и в обратном направлении).

Для плоской произвольной системы сил, приложенных к балке, составляем три уравнения равновесия:

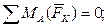
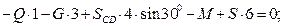
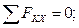
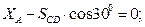
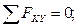
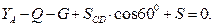
Решив систему уравнений, получим:

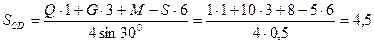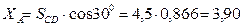кН.

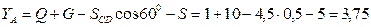кН.

кН.

Значения 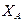, , 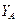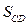получились положительными. Следовательно, принятые направления этих сил совпадают с их действительными направлениями.

Пример 2. Жесткая рама АВ (рис. 10) находится в равновесии. Интенсивность распределенной нагрузки q=1 кН/м, момент пары сил М=10 кН*м, Р=5 кН, 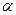=60⁰; размеры – в м. Определить реакции жесткой заделки А.

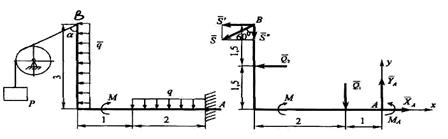Рисунок 10 – К примеру 2 Рисунок 11 – К примеру 2

Решение: Рассмотрим равновесие жесткой рамы АВ (рис. 10). Укажем задаваемые силы, действующие на раму. Такими силами будут являться равнодействующие равномерно распределенных нагрузок на горизонтальном и вертикальном участках рамы – силы 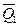и 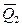, по модулю равные кН, 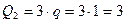кН и приложенные в серединах соответствующих участков; пара сил с моментом М; сила 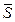натяжения троса, по модулю равная 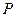и направленная вдоль троса от рамы. Отбрасываем связь – жесткую заделку в точке А. Действие жесткой заделки заменяем ее реакциями: двумя составляющим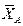и и 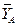силы и парой с моментом 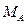. Для удобства составления уравнения моментов силу 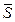раскладываем на составляющие 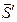и 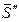(рис. 11), по величине равные:

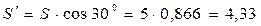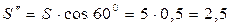кН,

кН.

Три уравнения равновесия будут иметь вид:

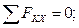
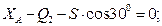
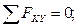
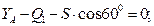
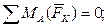
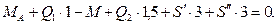
Из уравнений получаем:

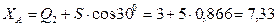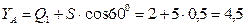кН;

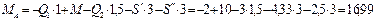кН;

кН.

Кинематика точки

Для изучения движения точки применяются три способа [1]:

1) Векторный способ. Положение точки определяется её радиусом-вектором 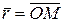относительно некоторого неподвижного центра О в рассматриваемой системе отсчёта (рис. 24). При движении точки радиус-вектор 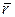изменяется, т.е. является векторной функцией времени:

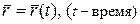. (13)

Уравнение (13) называется векторным уравнением движения точки. Траекторией точки является геометрическое место концов радиуса-вектора 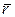, построенное в выбранной системе отсчёта, т.е. годограф вектора .

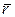Скорость и ускорение точки при заданном уравнении движения (13) равны:

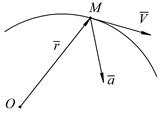
Рисунок 24 – Система отчета

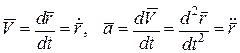(14)

Вектор скорости 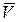направлен по касательной к траектории в сторону движения. Вектор ускорения 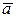всегда направлен в сторону вогнутости траектории точки или по её касательной (рис. 24). Векторный способ изучения движения точки обычно применяется в теоретических выкладках.

2) Координатный способ. Положение точки в выбранной, например, прямоугольной декартовой системе координат OXYZ определяется координатами:

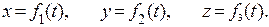(15)

При движении точки её координаты являются функциями времени. Выражения (15) называются уравнениями движения точки в координатной форме. Уравнение траектории точки получается из уравнений движения (15) исключением из них времени t как параметра.

Скорость и ускорение точки определяются через их проекции на оси координат:

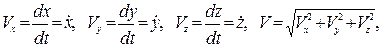(16)

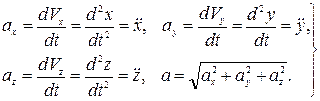(17)

Модуль касательного ускорения точки можно вычислить по формуле:

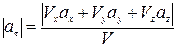. (18)

Нормальное ускорение точки определяется через полное и касательное ускорения:

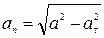. (19)

Из формулы 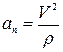определяется радиус кривизны траектории:

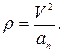(20)

План решения задач

1) По заданным уравнениям движения точки (как правило, на плоскости) исключением из них времени t получить уравнение траектории точки.

2) В выбранном масштабе изобразить траекторию на рисунке.

3) Определить положение точки в заданный момент времени. Для чего следует подставить этот момент в уравнения движения и вычислить координаты точки. По найденным координатам изобразить положение точки на траектории.

4) По формулам (16) – (20) для заданного момента времени определить:

– скорость точки;

– ускорение точки;

– касательное и нормальное ускорения точки;

– радиус кривизны траектории.

5) В масштабе изобразить на рисунке в ранее найденном положении точки векторы скорости, полного, касательного и нормального ускорений.

3) Естественный способ. Положение точки на заданной траектории определяется дуговой координатой S (рис. 25). Уравнение движения точки в естественной форме имеет вид:

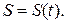(21)

Проекция скорости точки на направление орта касательной 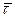и модуль скорости определяются следующим образом:

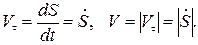(22)

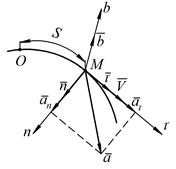
Рисунок 25 – Положение точки на заданной траектории

Проекции ускорения на оси естественного трёхгранника, а также модуль полного ускорения определяются по формулам:

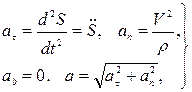(23)

где r – радиус кривизны траектории точки.

План решения задач

1) Определить положение точки на траектории в заданный момент времени. Для этого следует подставить этот момент времени в уравнение движения (21) и вычислить дуговую координату точки. Изобразить найденное положение точки на траектории.

2) По формулам (22), (23) для заданного момента времени определить следующие величины:

– скорость точки;

– касательное, нормальное и полное ускорения точки.

3) В выбранном масштабе изобразить на рисунке в рассматриваемом положении векторы скорости, касательного, нормального и полного ускорений точки.

Пример 1. Движение точки М задано уравнениями:

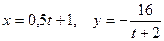, (24)

где x, y – в см,

t – в с.

Определить траекторию, скорость, полное, касательное и нормальное ускорения точки, а также радиус кривизны траектории в момент времени t= 2c.

Решение:. Находим уравнение траектории движения точки. Для этого исключаем из уравнений движения (24) время t, а именно:

.

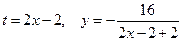Окончательно уравнение траектории имеет вид:

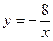, (25)

При этом в соответствии с уравнениями движения (24) координаты точки должны удовлетворять условиям:

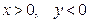. (26)

На рисунке 26 изображаем траекторию в виде гиперболы, расположенной согласно условиям (26) в четвёртом квадранте.

Вычисляем координаты точки для момента времени t = 2с:

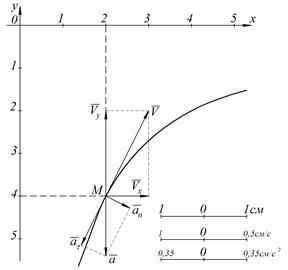
Рисунок 26 – К примеру1

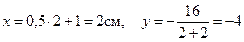см.

По найденным координатам изображаем точку на траектории (рис.26).

Далее по формулам (16) определяем скорость точки:

.

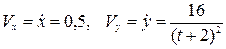В момент времени t = 2 с:

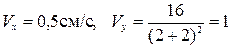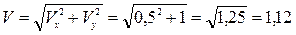см/с,

см/с.

Аналогично, в соответствии с формулами (17), находим полное ускорение:

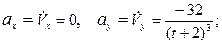
при t = 2 с:

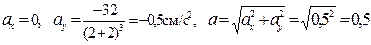см/с².

Определяем по формулам (18), (19) касательное и нормальное ускорения точки:

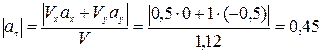см/с²,

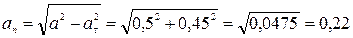см/с².

Находим радиус кривизны траектории. По формуле (1.8) имеем:

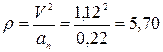см.

Найденные векторы скорости, полного, касательного и нормального ускорений точки в выбранном масштабе показываем на рисунке 26.

План решения задачи

1) Найти момент времени t₁, в который путь, пройденный грузом 1, будет равен S.

2) Определить в виде функций от времени следующие величины:

– скорость груза 1;

– угловую скорость колеса 2;

– угловую скорость и угловое ускорение колеса 3.

3) Вычислить значение угловой скорости и углового ускорения колеса 3 для момента времени t = t₁;

4) По формулам (30), (31) определить скорость, касательное, нормальное и полное ускорения точки М.

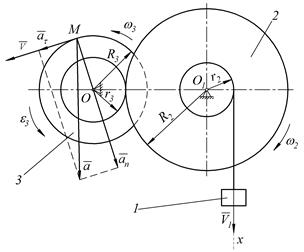
Рисунок 28 – К примеру 1.

Решение: Находим момент времени t₁, когда S = 10 см:

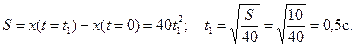
Определяем скорость груза 1:

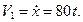
Далее находим угловую скорость колеса 2, исходя из нерастяжимости нити и, следовательно, равенстве скорости груза 1 и точки на ободе колеса 2 радиуса r₂, т.е. 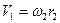. Тогда:

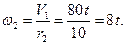
Направление угловой скорости соответствует направлению скорости груза 1 (рис. 28).

Считаем, что колёса 2 и 3 находятся в зацеплении без проскальзывания. Следовательно, скорость общей точки колёс одинакова, т.е.:

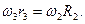
Откуда определяем угловую скорость и угловое ускорение колеса 3:

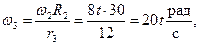
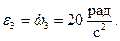
В момент времени t₁ = 0,5 с:

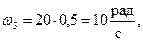
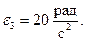
Вследствие зацепления колёс 2 и 3 направление угловой скорости 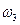соответствует направлению угловой скорости 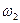, как показано на рисунке 2.2. Угловое ускорение 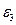направлено по угловой скорости 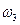, т.к. величины 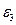и 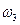одинакового знака. По формулам (30) и (31) определяем скорость, касательное, нормальное и полное ускорения точки М:

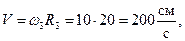
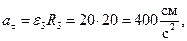
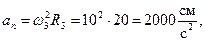
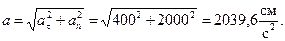
Вектор скорости направлен перпендикулярно радиусу ОМ в сторону вращения колеса 3 (рис. 28), нормальное ускорение – по радиусу к центру колеса, а касательное – перпендикулярно радиусу по направлению углового ускорения .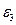

При плоском движении

Скорости двух точек А и В плоской фигуры (твёрдого тела) связаны между собой равенством :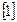

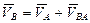, (32)

где 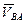– скорость точки В при вращении тела вокруг точки (полюса) А, определяемая формулой:

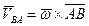. (33)

В выражении (33) 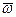– вектор угловой скорости тела, перпендикулярный плоскости движения. Из формулы (3.2) следует, что 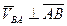и 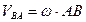. На рисунке 29 показана векторная зависимость (3.1).

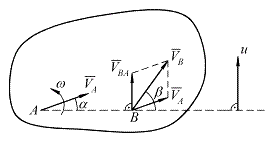
Рисунок 29 – Векторная зависимость

Формула (32) позволяет определить скорость точки В по известной скорости 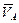и угловой скорости тела w.

Проецируя равенство (32) на прямую АВ и ось u, перпендикулярную АВ, получаем:

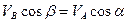, (34)

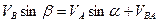, (35)

где .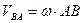

Решая систему уравнений (34) и (35), определяем b и V_B, т.е. направление и модуль скорости точки В:

,

.

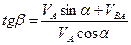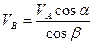Если известны модули и направления скоростей точек А и В, то из уравнения (35) можно найти угловую скорость тела, а именно:

.

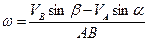Равенство (34) по сути выражает собой теорему о проекциях скоростей точек твёрдого тела, согласно которой проекции скоростей точек твёрдого тела на прямую, проходящую через эти точки, равны между собой. Многие задачи на определение скоростей точек твёрдого тела при плоском движении могут быть решены при помощи этой теоремы.

Второй метод решения указанных задач основан на использовании понятия мгновенного центра скоростей (МЦС) плоской фигуры. При непоступательном движении плоской фигуры (w¹ 0) в каждый момент времени существует точка тела, скорость которой равна нулю [1]. Эта точка называется мгновенным центром скоростей и, обычно, обозначается буквой Р. Принимая мгновенный центр скоростей за полюс, из равенства (32) получаем более короткую формулу для определения скоростей точек тела при плоском движении, т.е.:

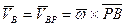. (36)

Из выражения (36) следует, что в каждый момент времени скорость любой точки твёрдого тела при плоском движении равна её скорости в мгновенном вращении тела вокруг мгновенного центра скоростей (рис. 30). Модули скоростей точек А и В тела будут определяться по формулам:

. (37)

Из выражений (37) следует зависимость:

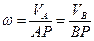. (38)

Выражения (37) ,(38) используются при решении задач.

План решения задач методом проекций

1) Выбрать за полюс точку плоской фигуры, скорость которой известна или легко находится из условия задачи.

2) Найти другую точку плоской фигуры, направление скорости которой также известно или легко определяется.

3) Для этой точки записать векторную формулу скорости вида (3.1) и спроецировать её на прямую, проходящую через полюс и рассматриваемую точку, а также на ось, перпендикулярную этой прямой.

4) Из полученных в п. 3 двух уравнений вида (34) (теорема о проекциях скоростей точек твёрдого тела) и (35) определить скорость рассматриваемой точки и угловую скорость плоской фигуры в данном положении.

5) Зная угловую скорость фигуры и скорость полюса, найти с помощью формулы вида (32) путём проецирования её на оси выбранной системы координат скорости других точек плоской фигуры.

План решения задач

При плоском движении

Ускорения двух любых точек А и В плоской фигуры (твёрдого тела) связаны между собой зависимостью [1]:

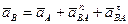, (39)

где 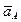– ускорение точки А (полюса);

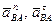– нормальное и касательное ускорения точки В при вращении фигуры вокруг полюса А.

При этом:

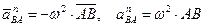; (40)

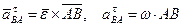, (41)

где w – угловая скорость тела,

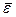– вектор углового ускорения тела, направленный перпендикулярно плоскости движения.

Вектор 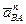всегда направлен от точки В к полюсу А,

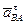– перпендикулярно отрезку АВ в сторону углового ускорения тела.

На рисунке 37 показана векторная зависимость (39), где введено обозначение 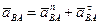– полное ускорение точки В при вращении фигуры вокруг полюса А.

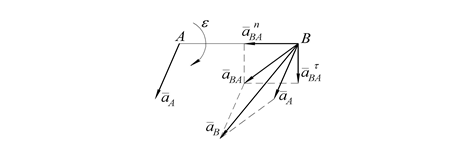
Рисунок 37 – Векторная зависимость

Таким образом, для определения ускорения произвольной точки В необходимо знать ускорение какой-либо другой точки А плоской фигуры, принимаемой за полюс, а также мгновенные угловую скорость w и угловое ускорение e фигуры. Тогда, складывая три вектора 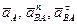(рис. 37), находим искомое ускорение точки В как сумму этих векторов.

Такой способ применим в случае, если угол поворота тела задан в виде функции о времени 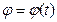, так как тогда можно определить 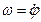и .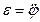

Во многих задачах зависимость 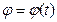неизвестна, и мгновенная угловая скорость w может быть найдена только для данного положения тела. В этом случае мгновенное угловое ускорение e тела не может быть найдено непосредственно.

Задачи на определение ускорений точек твёрдого тела, тем не менее, могут быть решены, если кроме известного ускорения полюса также будет известна траектория какой-либо другой точки тела (прямолинейная или криволинейная). Проецируя в этом случае равенство (39) на направление отрезка АВ, получаем уравнение с одним неизвестным 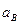(если траектория точки В прямолинейна) или 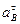(если траектория точки В криволинейна). При криволинейной траектории ускорение точки В раскладывается на нормальное и касательное ускорения, т.е.:

,

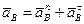где 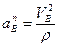(r – радиус кривизны траектории точки В).

Далее составляем второе уравнение проекций (39) на направление 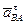, перпендикулярное к АВ. В этом уравнении будет одно неизвестное 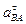, после определения которого находится угловое ускорение тела e в данный момент времени по формуле:

.

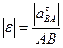В дальнейшем определение ускорений других точек тела также выполняется по формуле вида (39).

План решения задач

Тип I. Заданы скорость и ускорение одной точки плоской фигуры (или они легко находятся из условия задачи) и траектория другой точки фигуры. Требуется определить ускорения каких-либо точек фигуры.

1) Найти мгновенный центр скоростей тела и по заданной скорости точки тела и расстоянию от неё до МЦС по формуле (3.7) определить мгновенную угловую скорость w плоской фигуры. Если фигура совершает в данном положении мгновенно-поступательное движение, то w = 0.

2) Определить скорость точки тела (пусть точка В), заданная траектория которой криволинейна.

3) Найти нормальное ускорение точки В по формуле:

,

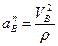где r – радиус кривизны траектории точки В.

При этом вектор 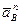направлен по нормали к траектории к центру кривизны.

4) Выбрать за полюс точку тела (например, точку А), ускорение которой известно или легко находится из условия задачи, и записать векторное выражение (39) для ускорения точки В, т.е.:

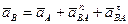. (42)

В случае криволинейных траекторий точек А и В, выражение (42) принимает вид:

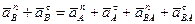. (43)

В векторных уравнениях (42) и (43) ускорения