Регуляторы. Понятие о законах регулирования

Распространенным способом синтеза САР является использование типовых регуляторов с последующей их настройкой на заданные характеристики системы.

В системах с обратной связью регулятор на основе ошибки рассогласования x(t) формирует регулирующее воздействие на объект u(t). Функциональную зависимость, связывающую эти величины, называют законом регулирования. При этом инерционность элементов регулятора не учитывают, то есть закон регулирования формулируют для установившегося или близкого к нему режима.

Различают непрерывные и дискретные регуляторы. Для непрерывных регуляторов в зависимости от способа формирования регулирующего воздействия различают следующие законы регулирования.

1. Пропорциональное регулирование (П-регулирование)

Регулирующее воздействие пропорционально рассогласованию:

.

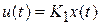Передаточная функция регулятора .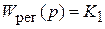

Как видно из передаточной функции, регулятор является статическим, то есть работает со статической ошибкой, это является основным недостатком регулятора. Его основными достоинствами являются простота, высокое быстродействие и устойчивость.

Обычно П-регуляторы используют в системах с малоинерционными объектами, так как для повышения точности требуется увеличивать коэффициент передачи. Чем меньше инерционность объекта, тем больше можно задать коэффициент передачи без потери устойчивости системы.

2. Интегральное регулирование (И-регулирование)

Регулирующее воздействие пропорционально интегралу рассогласования:

.

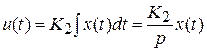Передаточная функция регулятора .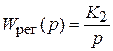

Как видно из передаточной функции, которая аналогична передаточной функции интегрирующего звена, регулятор является астатическим, то есть его статическая ошибка равна нулю, это является основным достоинством регулятора. Его основными недостатками являются низкое быстродействие и устойчивость.

Низкое быстродействие связано с тем, что в П-регуляторе требуемое значение управляющего воздействия достигается мгновенно, а в И-регуляторе на это затрачивается время Т_и = 1/K₂ (рис. 5.1).

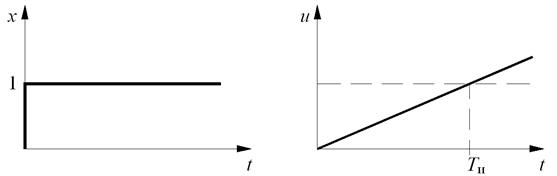
Рис. 5.1. Интегральное регулирование

Плохая устойчивость связана с тем, что интегрирующее звено, аналогично которому работает И-регулятор, вводит в систему отрицательный фазовый сдвиг –90°. Если объект не имеет самовыравнивания, то есть также является интегрирующим звеном, система становится структурно неустойчивой.

Обычно И-регуляторы используют в системах с малоинерционными объектами с самовыравниванием.

3. Пропорционально-интегральное или изодромное регулирование (И-регулирование)

Регулирующее воздействие пропорционально рассогласованию и его интегралу:

.

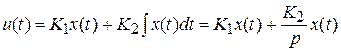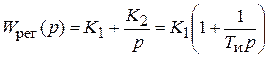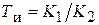Передаточная функция регулятора , где – время изодрома, то есть время удвоения пропорциональной составляющей регулирующего воздействие или время, на которое ПИ-регулятор опережает И-регулятор при ступенчатом входном воздействии (рис. 5.2).

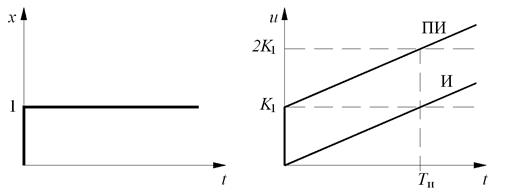
Рис. 5.2. ПИ-регулирование

Как видно из передаточной функции, которая аналогична передаточной функции изодромного звена, регулятор является астатическим, то есть его статическая ошибка равна нулю. В области низких частот ПИ-регулятор работает как И-регулятор, в области высоких – как П-регулятор, то есть высокая точность И-регулятора в статике сочетается с хорошей устойчивостью и быстродействием П-регулятора в динамике.

4. Пропорционально-дифференциальное регулирование (ПД-регулирование)

Регулирующее воздействие пропорционально рассогласованию и его производной:

.

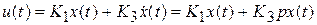Передаточная функция регулятора 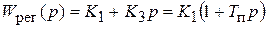, где 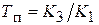– время предварения, то есть время, на которое ПД-регулятор опережает П-регулятор при линейно изменяющемся входном воздействии (рис. 5.3).

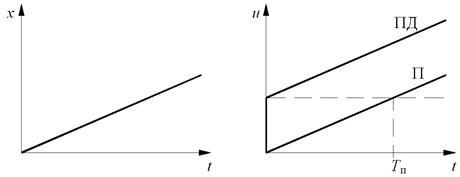
Рис. 5.3. ПД-регулирование

ПД-регулятор является статическим, потому имеет невысокую точность и помехоустойчивость за счет усиления высоких частот. Наличие дифференциальной составляющей улучшает работу в динамике, что выражается в повышении быстродействия (видно из рис. 3) и устойчивости за счет положительного фазового сдвига. В связи с этим ПД-регуляторы используют в системах с высокоинерционными объектами.

5. Пропорционально-интегрально-дифференциальное регулирование (ПИД-регулирование)

Регулирующее воздействие пропорционально рассогласованию, его интегралу и производной:

.

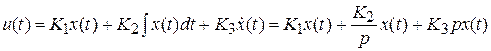Передаточная функция регулятора

.

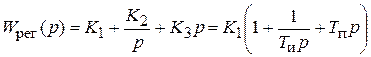ПИД-регулятор является астатическим и сочетает высокую точность И-регулятора в статике и хорошую устойчивость и быстродействие П-регулятора в динамике с положительным действием Д-составляющей. Вместе с тем для повышения помехоустойчивости следует соблюдать соотношение .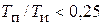

ПИД-регуляторы благодаря своим достоинствам являются наиболее распространенными наряду с ПИ-регуляторами.

Система, построенная на основе типовых регуляторов имеет структуру, показанную на рис. 5.4.

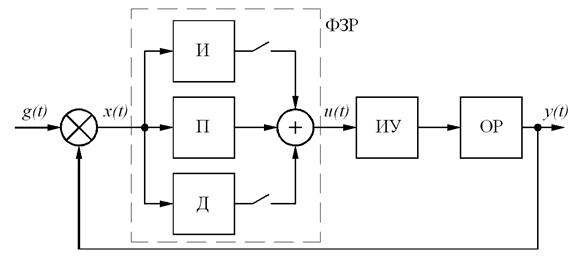
Рис. 5.4. САР на основе типового регулятора

Основой системы является формирователь закона регулирования ФЗР, состоящий из типовых блоков – пропорционального П, интегрального И и дифференциального Д, сигналы от которых суммируются. Переключатели позволяют задать требуемый закон регулирования, а также используются при настройке. Выбор закона регулирования производится в соответствии с параметрами объекта регулирования, который описывается передаточной функцией .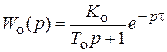

Для настройки регулятора с целью получить заданное качество системы используют различные методики. Настроечными параметрами являются коэффициент передачи регулятора K_р = K₁, время изодрома T_и и время предварения T_п (фирмы-производители регуляторов также предлагают другие параметры настройки своих моделей). В качестве примера рассмотрим расчетный и экспериментальный методы настройки.

При использовании расчетного метода задаются одним из требуемых критериев качества: колебательный переходный процесс с перерегулированием σ = 20 %; апериодический переходный процесс (σ = 0); минимальное значение интегральной оценки (I_min). Затем в соответствии с параметрами объекта регулирования и закона регулирования рассчитывают настройки регулятора, как показано в таблицах 5.1 (объекты с самовыравниванием) и 5.2 (объекты без самовыравнивания).

Таблица 5.1

Тип регулятора	Формулы для настройки
σ = 0	σ = 20 %	Imin
И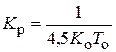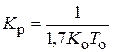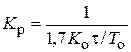
П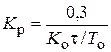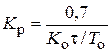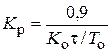
ПИ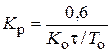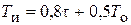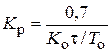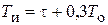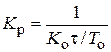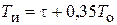
ПИД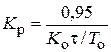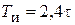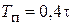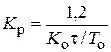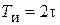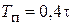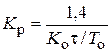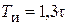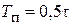

Таблица 5.2

Тип регулятора	Формулы для настройки
σ = 0	σ = 20 %	Imin
П			–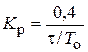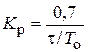
ПИ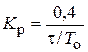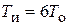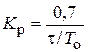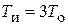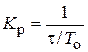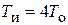
ПИД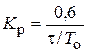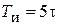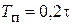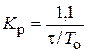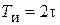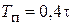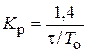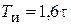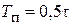

Расчетный метод применим, когда точно известны параметры объекта регулирования. Если объект плохо изучен, можно использовать экспериментальные методы настройки, например метод незатухающих колебаний. В этом случае отключают интегральную и дифференциальную составляющую и увеличивают К_р до появления на выходе системы незатухающих колебаний с периодом Т_кр, то есть до критического значения К_кр. Параметры настройки рассчитывают исходя из параметров полученного критического режима, как показано в таблице 5.3.

Таблица 5.3

Тип регулятора	Параметры настройки
П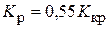
ПИ	;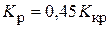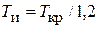
ПИД	; ;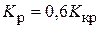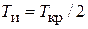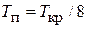

Коррекция САР

Коррекцию САР выполняют для получения системы с заданными свойствами. Для этого в систему вводят дополнительные корректирующие звенья. По способу их включения различают параллельные (включаются параллельно другим элементам системы), последовательные(включаются последовательно с другими элементами системы), встречно-параллельные (включаются в виде местных обратных связей) корректирующие звенья.

Коррекцию с помощью ЛАЧХ выполняют в следующей последовательности:

1) по заданным показателям качества строят желаемую ЛАЧХ и определяют передаточную функцию желаемой системы;

2) графики желаемой и исходной ЛАЧХ располагают в одной координатной плоскости и, сравнивая графики, определяют параметры корректирующих звеньев.

Построение желаемой ЛАЧХ выполняют по участкам.

Низкочастотный участок строится по заданным требованиям точности. Для этого рассчитывают координаты рабочей точки A_р 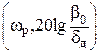. Рабочая частота – это максимальная частота входного синусоидального сигнала, при котором динамическая ошибка системы d_д ещё не должна быть больше заданной. При проектировании следящей системы угла поворота с астатизмом первого порядка:

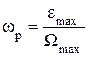
где W_max – максимальная частота вращения вала; e_max – его максимальное угловое ускорение.

Амплитуда входного сигнала определяется по формуле:

.

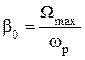Низкочастотный участок проводят через рабочую точку (или на 3 дБ выше, чтобы учесть погрешность аппроксимации ЛАЧХ ломаной). Для системы с астатизмом 1-го порядка НЧ участок имеет вид прямой со спадом –20 дБ/дек (рис. 5.5).

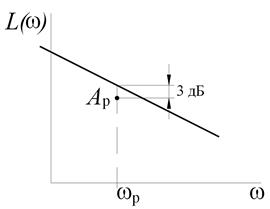
Рис. 5.5. Низкочастотная часть желаемой ЛАЧХ

Среднечастотный участок строится по заданным показателям быстродействия и запасов устойчивости. Например, если задано время регулирования t_р и запас устойчивости по фазе DF, частоту среза найдем, исходя из заданного времени переходного процесса t_p:

,

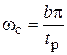где b – коэффициент, находимый из номограммы Солодовникова по допустимому перерегулированию s » 70 – DF (DF – необходимый запас по фазе). Номограмма Солодовникова показана на рис. 5.6.

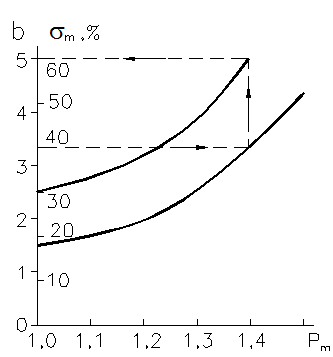
Рис. 5.6. Номограмма Солодовникова и пример определения по ней коэффициента b при σ = 40%; (Р_m – значение максимума ВЧХ)

Частоты начала и конца среднечастотного участка ЖЛАЧХ определим по уравнениям:

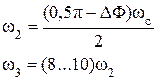
Среднечастотный участок проводится через частоту среза под наклоном –20 дБ/дек (рис. 5.7).

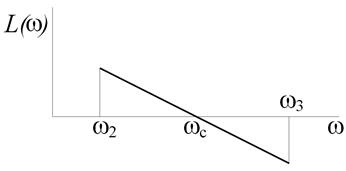
Рис. 5.7. Среднечастотная часть желаемой ЛАЧХ

НЧ и СЧ участки соединяются участком под наклоном –40 дБ/дек (если при этом рабочая точка оказывается выше графика, выбирается больший наклон).

Высокочастотный участок определяет интенсивность подавления помех и проводится параллельно высокочастотному участку исходной ЛАЧХ.

В итоге желаемая ЛАЧХ для системы с астатизмом 1-го порядка имеет вид, показанный на рис. 5.8.

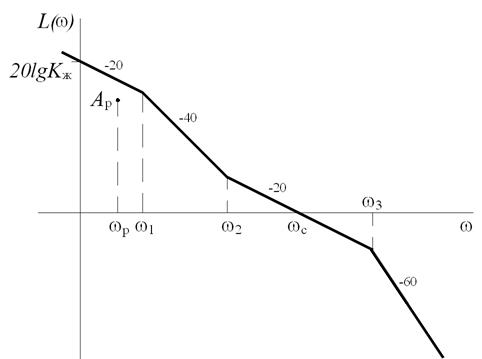
Рис. 5.8. Желаемая ЛАЧХ

По желаемой ЛАЧХ можно записать передаточную функцию желаемой системы:

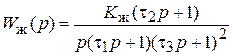, где .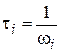

При последовательной коррекции (рис. 5.9):

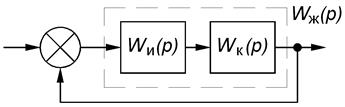
Рис. 5.9. Последовательная коррекция

,

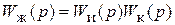где W_и(p) – передаточная функция исходной системы, W_ж(p) – передаточная функция желаемой системы, W_к(p) – передаточная функция корректирующего устройства.

.

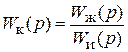При использовании ЛАЧХ:

.

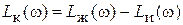При встречно-параллельной коррекции исходную систему делят на две части – изменяемую с передаточной функцией W_изм(p) и неизменяемую с передаточной функцией W_н(p) (рис. 5.10):

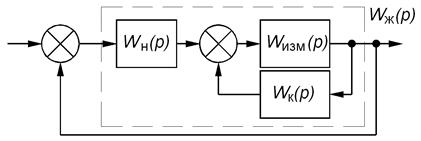
Рис. 5.10. Встречно-параллельная коррекция

.

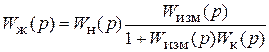Для упрощения формулы предположим, что в рабочем частотном диапазоне системы W_изм(p)W_к(p) >> 1. Тогда

.

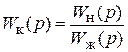При использовании ЛАЧХ:

.

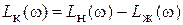Полученные таким образом характеристики корректирующих устройств являются сложными для реализации, поэтому чаще коррекцию выполняют в следующем порядке.

1. Располагают ЛАЧХ исходной и желаемой системы в одной координатной системе (рис. 5.11). Здесь предполагается, что исходная система имеет структуру, показанную на рис. 5.12 и передаточную функцию 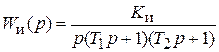. Для примера взята следящая САР угла поворота, состоящая из датчика рассогласования, усилителя, электродвигателя и редуктора.

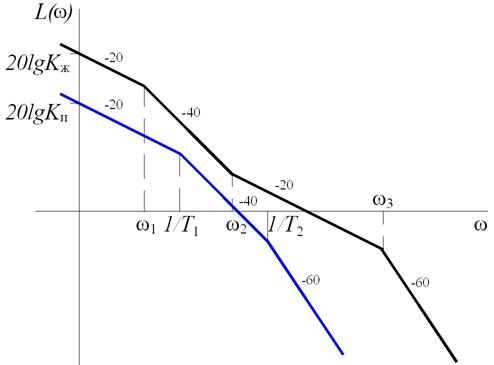
Рис. 5.11. Расположение желаемой и исходной (синяя) ЛАЧХ

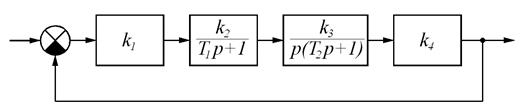
Рис. 5.12. Исходная САР

2. Увеличивают коэффициент передачи исходной системы до совпадения низкочастотных участков ЛАЧХ (рис. 5.13).

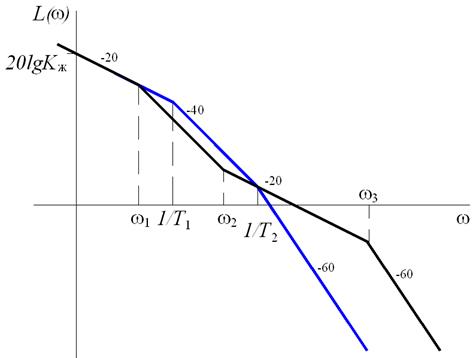
Рис. 5.13. Повышение коэффициента передачи исходной системы

3. С помощью местных обратных связей изменяют постоянные времени элементов исходной системы таким образом, чтобы получить расположение ЛАЧХ, показанное на рис. 5.14,а или 5.14, б.

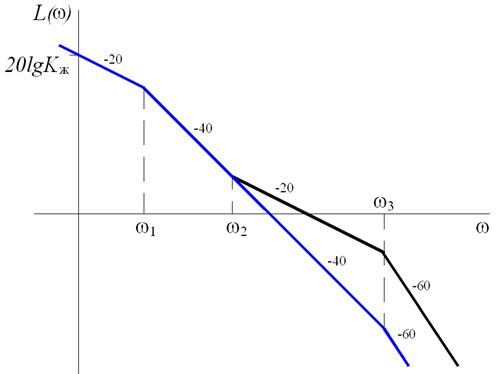
а)

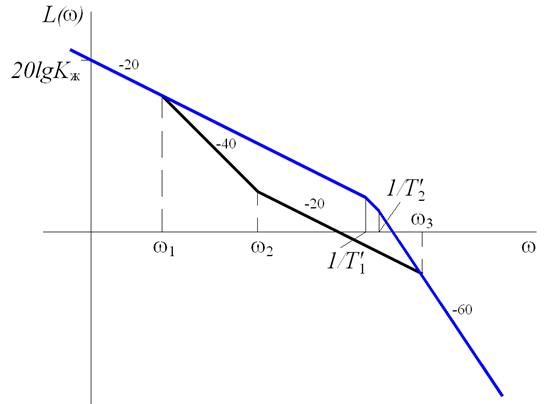
б)

Рис. 5.14. Изменение исходной ЛАЧХ местными обратными связями

В первом случае T₁ увеличивается до значения t₁, T₂ уменьшается до t₃. Во втором случае обе постоянные времени уменьшаются. Для определения новых постоянных времени воспользуемся формулами для встречно-параллельного соединения звеньев (рис. 5.15).

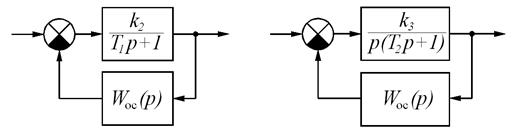
Рис. 5.15. Местные обратные связи

Для апериодического звена:

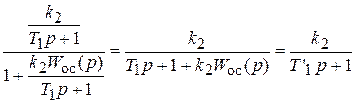
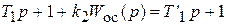
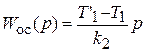
Для обратной связи используется дифференцирующее звено.

Для интегрирующего звена:

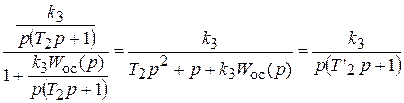
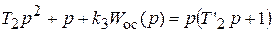
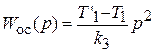
Для обратной связи используется дифференцирующее звено второго порядка.

4. Вычитанием исходной ЛАЧХ из желаемой получают ЛАЧХ последовательного корректирующего звена (рис. 5.16).

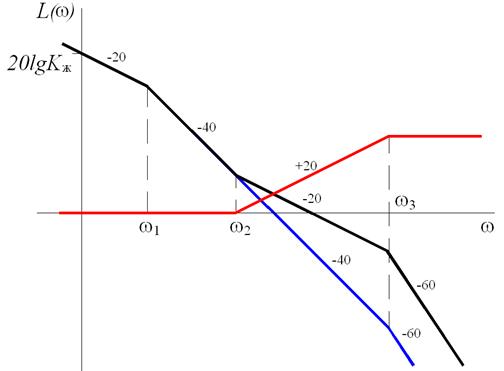
а)

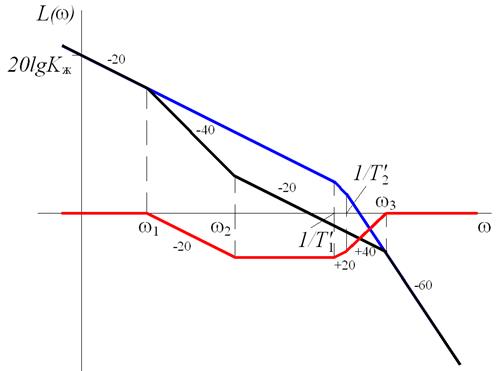
б)

Рис. 5.16. ЛАЧХ корректирующих устройств

Передаточная функция корректирующего устройства для рис. 8, а

,

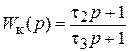для рис. 8, б

.

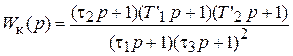Во втором случае КУ сложнее, однако, в первом варианте оно усиливает высокочастотные помехи.

Скорректированная система имеет структуру, показанную на рис. 5.17.

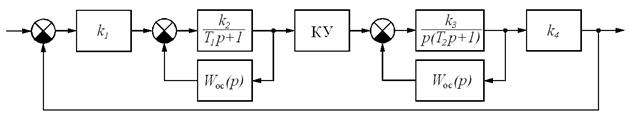
Рис. 5.17. Структурная схема скорректированной САР

Литература: [1, c. 150 – 194] , [2, c. 101 – 123], [3. с. 476 – 484]

НЕЛИНЕЙНЫЕ САУ

Типовые нелинейности

Нелинейной называется система, которая содержит хотя бы один элемент, нелинейностью которого невозможно пренебречь.

К нелинейным звеньям относятся устройства, имеющие следующие особенности характеристики.

1. Люфт (мертвый ход, петля гистерезиса).

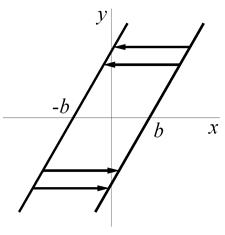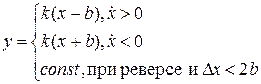Такая характеристика встречается в механических характеристиках из-за влияния зазоров (зубчатые передачи), а также в электромагнитных системах.

2. Мертвая зона (зона нечувствительности).

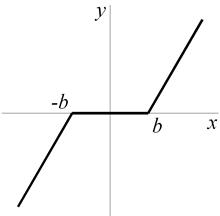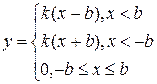b – порог чувствительности.

Характерна для большого количества элементов (например, для измерительных преобразователей).

3. Насыщение.

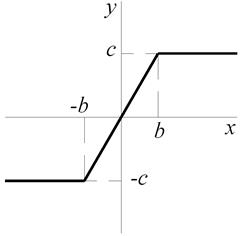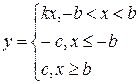Такая характеристика описывает работу усилителей, а также электромагнитных систем.

4. Релейные характеристики.

Их особенность – скачкообразное изменение выходной величины при плавном изменении входной.

4.1. Идеальное трехпозиционное реле

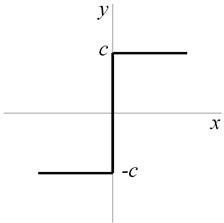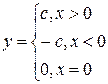4.2. Трехпозиционная характеристика с мертвой зоной.

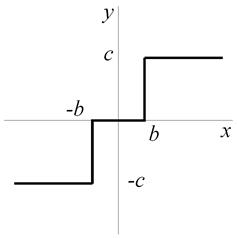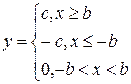4.3. Трехпозиционная характеристика с мертвой зоной и гистерезисом.

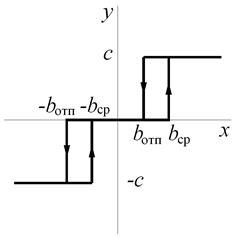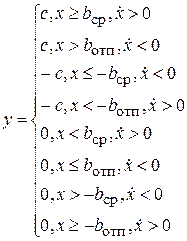4.4. Двухпозиционное реле.
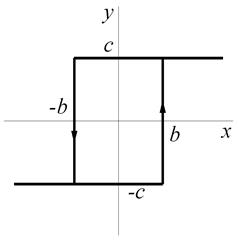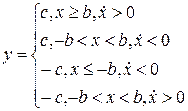