Принципы построения автоматических систем

АВТОМАТИКА

Конспект лекций

для студентов заочного отделения специальностей 1-38 01 01 «Механические и электромеханические приборы и аппараты», 1-38 02 03 «Техническое обеспечение безопасности», 1-54 01 01 «Метрология, стандартизация и сертификация», 1-38 02 01 «Информационно-измерительная техника»

Учебное электронное издание

Минск ◊ БНТУ ◊2012

УДК 681.513.3

ББК 34.9

М 54

Авторы:

В.Т. Минченя,

А.Л. Савченко,

Рецензенты:

И.А. Каштальян,

В.Г. Смирнов

Белорусский национальный технический университет

пр-т Независимости, 65, г. Минск, Республика Беларусь

Тел.(017) 232-77-52 факс (017) 232-91-37

Е-mail: …

http://www....

Регистрационный № _______

Издание предназначено в качестве учебно-методического пособия по дисциплине «Автоматика» для студентов заочного отделения специальностей 1-38 01 01 «Механические и электромеханические приборы и аппараты», 1-38 02 03 «Техническое обеспечение безопасности», 1-54 01 01 «Метрология, стандартизация и сертификация», 1-38 02 01 «Информационно-измерительная техника». Пособие содержит материалы, которые могут быть использованы при самостоятельном изучении некоторых разделов теоретического курса студентами как заочного, так и дневного отделения всех специальностей, изучающих дисциплину «Автоматика».

©БНТУ, 2012

© Минченя В.Т., Савченко А.Л., 2012

СОДЕРЖАНИЕ

ВВЕДЕНИЕ. 5

1. ИСТОРИЯ РАЗВИТИЯ АВТОМАТИКИ.. 7

2. ПРИНЦИПЫ ПОСТРОЕНИЯ АВТОМАТИЧЕСКИХ СИСТЕМ.. 13

2.1. Основные понятия и определения. 13

2.2. Обобщенная схема системы автоматического управления. 15

2.3. Фундаментальные принципы построения САУ.. 17

Принцип разомкнутого управления. 17

Принцип управления по возмущению (принцип компенсации). 20

Принцип управления по отклонению.. 22

Принцип комбинированного управления. 26

2.4. Классификация систем автоматического регулирования. 27

Системы стабилизации. 27

Программные системы.. 28

Следящие системы.. 30

3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ЛИНЕЙНЫХ САУ.. 40

3.1. Дифференциальные уравнения САУ.. 40

3.2. Динамические характеристики звеньев и САУ.. 41

Временные характеристики линейных звеньев. 43

Частотные характеристики звеньев. 44

Позиционные звенья. 45

Интегрирующие звенья. 51

Дифференцирующие звенья. 54

Звенья с запаздыванием. 56

3.3. Структурные схемы САУ.. 58

4. АНАЛИЗ КАЧЕСТВА САР. 65

4.1. Устойчивость систем автоматического регулирования. 65

Основные понятия об устойчивости. 65

Критерий устойчивости Гурвица. 67

Критерий устойчивости Михайлова. 69

Критерий устойчивости Найквиста. 71

Влияние параметров системы на устойчивость. 74

Определение области устойчивости методом D-разбиения. 76

4.2. Точность САР. Статическое и астатическое регулирование. 81

Ошибка в типовых режимах работы.. 81

Повышение точности САР. 90

4.3. Оценка качества регулирования. 93

Оценка качества по переходному процессу. 93

Частотные критерии качества. 95

Корневые критерии качества. 97

Интегральные оценки качества. 99

5. КОРРЕКЦИЯ ДИНАМИЧЕСКИХ СВОЙСТВ И СИНТЕЗ СИСТЕМ УПРАВЛЕНИЯ 101

5.1. Регуляторы. Понятие о законах регулирования. 101

5.2. Коррекция САР. 106

6. НЕЛИНЕЙНЫЕ САУ.. 116

6.1. Типовые нелинейности. 116

6.2. Методы исследования нелинейных САР. 118

7. ИМПУЛЬСНЫЕ И ЦИФРОВЫЕ САР. 125

7.1. Модели импульсных САР. 125

7.2. Анализ качества импульсных и цифровых САР. 128

8. АДАПТИВНЫЕ САР. 130

9. СИСТЕМЫ С НЕЧЕТКОЙ ЛОГИКОЙ (FUZZY LOGIC) 134

ЛИТЕРАТУРА.. 137

ВВЕДЕНИЕ

Для того чтобы различные технические устройства и системы выполняли требуемые функции необходимо организовать тот или иной процесс управления. Процесс управления может быть реализован «ручным» способом или с помощью совокупности технических средств, которые, в общем случае, называют системами автоматического управления.

Чтобы отличить управляемое от неуправляемого, обычно прибегают к понятию целесообразности, под которым понимают соответствие объекта определенному состоянию. Достижение этого состояния связано с воздействием процесса управления на объект. Управление может быть привнесено извне, а может быть присуще самому объекту. В последнем случае мы говорим о самоуправлении или автоматизме (от греч. самодействующий). Кибернетика, как правило, изучает самоуправляющиеся системы, т.е. такие, где хотя бы один элемент является самоуправляющимся, определяющим целесообразность управления объектом. Кибернетика – это наука об управлении в сложных динамических системах различной природы, где сложность понимается как наличие в системе разнородных элементов (человек, природа, техника) и разнообразных связей между ними (положительных, отрицательных, прямых, обратных и др.).В зависимости от класса объекта управления кибернетика подразделяется на техническую, организационную, экономическую, медицинскую и др.Техническая кибернетика (или теория автоматического управления) – отрасль науки, изучающая технические системы с помощью идей и методов кибернетики. Основная задача управления техническим объектом – найти и реализовать в данных условиях алгоритм управления, при котором выполняются требования, предъявляемые к процессу.Техническими средствами для реализации систем управления являются средства получения информации (датчики), ее передачи и обработки и средства регулирования (регуляторы, исполнительные механизмы, регулирующие органы).Необходимость внедрения и развитие систем автоматического управления способствовали созданию отдельного научно-технического направления, которое включает элементную базу, теоретические вопросы анализа и синтеза, вопросы проектирования и обеспечения требуемой надёжности.Вместе с тем, это отдельное направление имеет тесную связь с электроникой, электротехникой, математикой и другими разделами науки и техники.Дисциплина «Автоматика» является одной из базовых дисциплин в подготовке инженеров технических ВУЗов. Знания основ автоматики, методов анализа и синтеза систем автоматического управления и регулирования, необходимы при разработке и эксплуатации автоматического оборудования, при проектировании и расчете отдельных устройств, применяемых для автоматизации производственных процессов. Целью данной дисциплины является изучение круга вопросов, которые представляют собой разделы теории автоматического управления и регулирования. Рассматриваемые вопросы являются наиболее общими и характеризуют с единых позиций процессы, происходящие в системах автоматического управления и регулирования. В данной дисциплине предусмотрено изучение принципов построения, методов анализа и синтеза систем автоматического управления и регулирования.

Основные задачи изучения дисциплины:

– изучение методологии математического описания и структуры построения САУ и САР;

– изучение основных принципов и концепции построения систем автоматического управления;

– изучение принципов анализа и синтеза систем автоматического управления и регулирования;

– изучение основных проблем и перспектив развития теории автоматического управления (ТАУ) и регулирования (ТАР);

– изучение принципов действия основных устройств, обеспечивающих автоматизацию контроля, управления и регулирования производственными процессами в приборостроении;

После изучения дисциплины Вы должны уметь:

– выбрать и обосновать функциональную схему автоматической системы управления и регулирования;

– обоснованно выбирать структуры и схемы регулирования и управления физическими величинами;

– определять передаточные функции динамических звеньев и находить математическую модель системы в целом;

– производить исследование устойчивости, оценку качества и синтез линейных непрерывных и дискретных систем автоматического регулирования;

– производить выбор и расчет исполнительных механизмов следящих систем с учетом динамических свойств системы

ИСТОРИЯ РАЗВИТИЯ АВТОМАТИКИ

Слово «автоматика» происходит от древнегреческого «автоматос» – самодвижущийся. Термин «автоматическое» подразумевает, что управление осуществляется без вмешательства человека. Впервые сведения об автоматах появились в начале нашей эры в работах Герона Александрийского (жил где-то между 200–300 г.г. н.э.) (греческий математик и механик, изобрел автоматический театр кукол, паровую турбину, первым начал создавать программируемые устройства – вал со штырьками с намотанной на него веревкой) «Пневматика» и «Механика», где описаны автоматы, созданные самим Героном и его учителем Ктесибием (греческий писатель и механик): пневмоавтомат для открытия дверей храма, водяной орган, автомат для продажи святой воды и др. Идеи Герона значительно опередили свой век и не нашли применения в его эпоху. В средние века значительное развитие получила так называемая «андроидная» автоматика, когда механики создали ряд автоматов, подражающих отдельным действиям человека, и, чтобы усилить впечатление, изобретатели придавали автоматам внешнее сходство с человеком и называли их «андроидами», т.е. человекоподобными.Вызывает интерес конструкция так называемых водяных часов. Время измерялось с помощью капель воды, падающих с постоянной скоростью через сопло из резервуара. Чтобы обеспечить постоянную скорость истечения воды, необходимо было поддерживать постоянный уровень воды в резервуаре, а для этого требовалось автоматическое регулирование. Интересно, что задача поддержания постоянного уровня жидкости в сосуде до сих пор сохраняет актуальность, и мы занимаемся проектированием соответствующих систем регулирования.Одна из возможных конструкций водяных часов показана на рис. 1.1.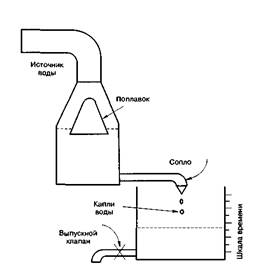

Рис. 1.1. Предполагаемая конструкция водяных часов

Плавающий клапан в верхнем сосуде, одновременно играющий роль датчика и исполнительного устройства системы регулирования, служит для поддержания постоянного уровня воды в этом сосуде. Когда уровень воды соответствует заданному значению, клапан закрывает питающую магистраль. Если же уровень меньше заданного, то клапан открывает магистраль, что приводит к повышению уровня.Вода через сопло капает в нижний сосуд, снабжённый проградуированной шкалой. Уровень воды в нём точно указывает промежуток времени с того времени, когда сосуд был пуст. Фактически накопление воды в нижнем резервуаре является операцией интегрирования (суммирования). Аналогичная процедура (суммирование) используется при численном интегрировании в цифровых компьютерах. Эта процедура использовалась 22 столетия назад, и в наши дни данный принцип лежит в основе работы современных компьютеров. Действительно, здесь трудно изобрести что-то новое. Так голландский механик и химик Корнелиус Дреббель (1572–1633) изобрёл регулятор температуры, который он использовал в своих химических опытах и в инкубаторах для выведения цыплят. Этот регулятор содержал устройство, позволявшее выпускать нагретый воздух из камеры, когда температура в ней достигала желаемого значения.В 1657 г. Х.Гюйгенс математик, физик, астроном (Гаага, Нидерланды, 1629–1695) встроил в часы маятниковый регулятор хода.Американец Уильям Генри (1729–1786) изобрёл регулятор температуры, в котором использовалась заслонка, автоматически управлявшая сгоранием топлива и, следовательно, температурой. Принцип действия датчика температуры и исполнительного устройства был основан на давлении нагретого воздуха при его расширении. Расширение воздуха приводило к закрытию заслонки и уменьшению сгорания топлива.В XVIII в. швейцарские часовщики Пьер Дро и его сын Анри создали механического художника и др.Прекрасный театр автоматов был создан в XVIII в. русским механиком-самоучкой Кулибиным. Его театр, хранящийся в Эрмитаже, помещен в «часах яичной фигуры».Но хотя отдельные автоматические регуляторы появились в давние времена, они оставались любопытными в истории эпизодами и серьезного влияния на формирования техники и теории автоматического управления не оказали. Изобретение первого в мире промышленного автоматического устройства относится к 1765 г. и принадлежит талантливому русскому механику И.И.Ползунову (Барнаул 1728–1766) (Российская империя). Этим автоматическим устройством был регулятор питания котла разработанной им двухцилиндровой паровой машины, автоматически поддерживающий уровень воды в котле независимо от интенсивности отбора пара. Предложенный в этом регуляторе принцип управления по отклонению до настоящего времени остается одним из основных принципов построения самых разнообразных автоматических устройств и систем. Усовершенствования регуляторов уровня осуществили также Саттон Томас Вуд в 1784 г. и Джеймс Бриндли в США. Главным изобретением в области управления скоростью ветряных мельниц и паровых машин считается центробежный регулятор скорости, предложенный в 1785 г. Джеймсом Уаттом (James Watt) (Шотландия, 1736–1819). (Уатт ввел первую единицу мощности – лошадиную силу, его именем названа единица мощности – Ватт). При увеличении скорости вращения машины шарики-грузы за счёт центробежной силы расходились, что, в свою очередь, приводило к перемещению втулки вверх по оси машины. При этом с помощью клапана, управляемого рычажным механизмом, уменьшалось подача пара и, следовательно, скорость вращения. Уменьшение скорости вращения приводило к обратному эффекту (рис. 1.2). Принцип работы регуляторов оказался одним и тем же, поэтому этот принцип регулирования иногда называют принципом Ползунова-Уатта.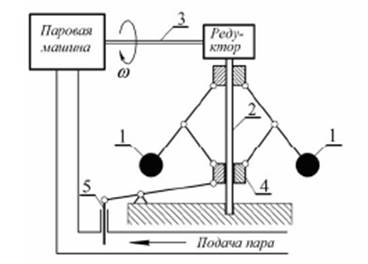 Рис. 1.2. Центробежный регулятор Уатта Регулятор состоит из двух грузов 1, подвешенных на шарнирах вдоль оси вертикального вала 2, связанного через редуктор с валом паровой машины, Рычаги грузов соединены с втулкой 4, которая может перемещаться вдоль вала 2. Втулка 4, в свою очередь, соединена рычагом с заслонкой 5, положение которой определяет сечение отверстия, через которое пар поступает из котла в цилиндр машины. При пуске паровой машины ее выходной вал 3 приходит во вращение с круговой скоростью ω, а каждый из грузов начинает испытывать воздействие двух сил: силы упругости рычага F (или ее вертикальной F_в и горизонтальной F_г составляющих) и силы веса P. (рис. 1.3). 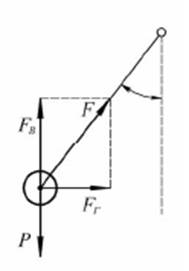Рис. 1.3. Схема сил, действующих на грузы в процессе работы машины Если величина веса P, угол α и передаточное число редуктора подобраны такими, что при этом F_в > P, то грузы начнут смещаться вверх и в стороны до тех пор, пока не наступит состояние динамического равновесия, когда F_в =P . В результате этого заслонка 5 принимает некоторое положение, соответствующее заданной скорости.Известны изобретения регуляторов давления для паровых котлов которые сделали Дени Папен (1647–1712), Роберт Делал в 1799 г. и Мэтью Мюррей в 1799 г.В 1808 г. Ж.Жаккаром было создано первое программное устройство управления ткацким станком от перфокарты (для воспроизведения узоров на коврах). Начиная со второй половины ХIХ века большую роль в развитии автоматики стали играть потребности зарождавшейся промышленной электротехники. Вместе с тем применение электричества чрезвычайно расширилось возможности построения сложных автоматических устройств. Электрические автоматические устройства начинают проникать буквально во все отрасли техники. Одним из первых электрических автоматов был электромагнитный регулятор частоты вращения вала паровой машины, разработанный в 1854 г. русским механиком и электротехником К.И.Константиновым (1819-1871).Однако во многих случаях разработанные регуляторы вместо того, чтобы поддерживать постоянное значение выходной переменной, позволяли ей совершать небольшие колебания относительно заданного значения. Этот эффект часто называли «рысканием». Чтобы устранить подобную неустойчивость, потребовалось создание математических моделей физических устройств, т.е. уравнений, решение которых описывало бы поведение этих устройств. В результате появились современные математические методы моделирования, анализа и синтеза систем управления. В разработку этих методов внесли свой вклад очень многие учёные. Пьер Симон Лаплас (1749–1827) изобрёл преобразование (названное впоследствии его именем), являющееся основой большинства методов анализа и синтеза систем управления. Брук Тейлор (1685–1731) – английский математик, именем которого названа найденная им формула, выражающая приращение функции в виде ряда, расположенного по возрастающим степеням приращения независимой переменной (ряды Тейлора).Джеймс Клерк Максвелл (1831–1879) – математическое моделирование и анализ.Основы научного подхода к проектированию автоматических устройств были заложены знаменитым русским ученым и инженером И.А.Вышнеградским (1830–1895) (впервые в университете ввел для студентов курсовое и дипломное проектирование), создал научные основы контуирования машин)), работа которого «Об общей теории регуляторов», изданная в 1876 г., положила начало теории автоматического управления.Исключительное значение в развитии теории автоматического управления имели труды А.М.Ляпунова (1857–1918, Ярославль, Российская империя, создал теорию устойчивости равновесия и движения механических систем с конечным числом параметров) об устойчивости движения. В 1892 г. появилась его работа «Общая задача об устойчивости движения», определившая целую эпоху в развитии ТАУ.Большое значение для формирования автоматики как науки имела работа великого русского ученого Н.Е.Жуковского «Теория регулирования хода машин», изданная в 1909 г., а также труды словацкого инженера А.Стодолы (1903), швейцарского математика А.Гурвица (1985 г.) и англичанина Эдварда Джона Рауса (1831–1907) (1877), Оливера Хевисайда (1850–1925) – математический анализ; Чарльза П. Стейнметца (1865–1923) – анализ частотных характеристик с помощью комплексных переменных; В начале 30-х годов теория автоматического регулирования (ТАР) обогатилась частотным аппаратом исследования. В 1932 г. появилась работа Гарри Найквиста (1889–1976), а в 1938–39 г.г. работы А.В.Михайлова (Критерий Михайлова), в которых предложены частотные критерии устойчивости систем автоматического регулирования. Идеи заложенные в этих работах получили свое дальнейшее развитие в трудах В.В.Солодовникова, Я.З.Цыпкина и др. В 1946 г. Хендрик У. Боде (1905–1982) (диаграмма Боде); и Л.Мак-Кол показали возможность применения логарифмических частотных характеристик при анализе свойств систем регулирования. В 50-е годы ХХ века В.В.Солодовников завершил формирование частотных методов анализа и синтеза САУ; в трудах А.А.Ляпунова, А.И.Лурье, А.М.Летова, М.А.Айзермана, В.М.Попова разработана теория нелинейных систем.С появление первых ЭВМ (1945 –США, 1951 –СССР, Лебедев С.А.) создаются сложные системы регулирования, экстремальные и оптимальные системы регулирования. В 60-е годы прошлого века Я.З.Цыпкин разработал основы теории дискретных систем. Г.В.Щипановым, В.С.Кулебакиным, Б.Н.Петроваым создана теория инвариантных систем, а Л.С.Понтрягин, А.А.Фельдбаум и А.А.Красовский разработали принципы экстремального управления и теорию оптимальных систем. С конца ХХ века началось внедрение в управление микропроцессоров и микроЭВМ. Появились сложные системы управления производственными процессами, развиваются новые разделы ТАУ, такие как динамика сложных систем, моделирование сложных систем и т.п. В качестве математического аппарата широко используется пространство состояния.Этот список ни в коей мере не является исчерпывающим как в персональном плане, так и в плане достижений в отдельных областях. Он лишь призван дать Вам сведения о том, какие идеи и в какое время разрабатывали перечисленные выше учёные. Список современных учёных, внёсших весомый вклад в развитие теории автоматического управления, был бы слишком длинным и, конечно, далеко не бесспорным. Следует отметить, что окончательное формирование автоматики в самостоятельную научную дисциплину относится к 40-вым годам. В 1960 г. в Москве состоялся Первый Международный конгресс по вопросам автоматического управления.

В настоящее время созданы и продолжают разрабатываться самоприспосабливающие, самонастраивающиеся сиcтемы. Известно, что наиболее cамонастраивающейся и самоприспосабливающей системой является живой организм, в связи с чем сформировалась отрасль кибернетики – бионика, изучающая процессы управления в живых организмах с тем, чтобы все лучшее что создала природа в процессе эволюции использовать при создании автоматических систем в технике.

В заключение отметим, что термин «автоматическое управление» следует отличать от термина «автоматизированное управление», под которым понимается управление с обязательным участием человека.

Литература: [1, c. 3, 8 – 10], [2, c. 9 –12]

Системы стабилизации

Система стабилизации – система, алгоритм функционирования которой содержит предписание поддерживать значение регулируемой величины постоянным. В этих случаях задающее воздействие g(t) = const, то есть g(t) = g°.

Уравнение стабилизирующей САР y(t) = c + kDx, где Dx – отклонение управляемой величины от заданной; k – коэффициент передачи системы.

Покажем на примере САР частоты вращения ДПТ (рис. 2.14).

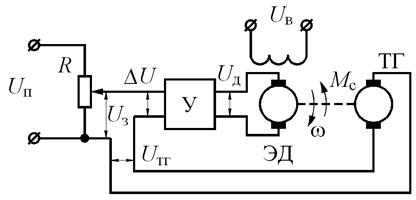
Рис. 2.14. Стабилизирующая САР

ω – частота вращения вала двигателя – регулируемая величина; М_с – момент нагрузки – возмущающее воздействие. Требуемый закон изменения регулируемой величины зависит от особенности ЭД. В данном случае требуется, чтобы ω = const = ω°. Основной причиной отклонения ω является изменение момента нагрузки на валу двигателя и U_п. Для изменения фактической ω используют ЧЭ – тахогенератор ТГ. U_тг = k_тгω.

R – потенциометр, выполняет функцию ЗУ.

DU = U_з– U_тг = U_з – k_тгω.

В правильно спроектированной САУ напряжение на входном усилителе при частоте ω = ω° ΔU ≈ 0.

Из уравнения U_з – k_тгω ≈ 0; ω = U_з/k_тг.

Скорость вращения ω пропорциональна U_з следовательно, если U_з = const, то и ω = const если k_тг = const.

Программные системы

Это системы регулирования, алгоритм которых содержит предписание изменять регулируемую величину в соответствии с заранее заданным законом. В данных системах g(t) = g°(t) – заранее известная функция времени или иногда некоторой другой величины.

Уравнение системы y = F(t), где F(t) – заданная функция времени. Чтобы получить программную систему, необходимо в стабилизирующей системе непрерывно изменять задающее воздействие так, чтобы в каждый момент времени регулируемая величина соответствовала заданному значению.

Чтобы изменять ЗВ необходимо перед ЗУ поставить программный элемент, схема которого показана ниже.

Рис. 2.15 – Общая схема устройства выработки программы управления

ДНП – датчик независимой переменной; ФП – функциональный преобразователь; ПЭ – промежуточный элемент (усиление, преобразование); ИЭ – исполнительный элемент, непосредственно воздействующий на объект назначения (задающее устройство САР).

Пример. Программная система регулирования температуры в камере.

Задающим устройством является потенциометр П, подвижный контакт которого перемещается кулачковым КМ. Потенциометр и чувствительный элемент (терморезистор ТР) включены в мост, напряжение с выхода которого усиливается усилителем У и питает нагревательный элемент НЭ. В роли ДНП выступает форма рабочей поверхности кулачка, а сам КМ с электродвигателем ЭД объединяют функции ФП и ИЭ.

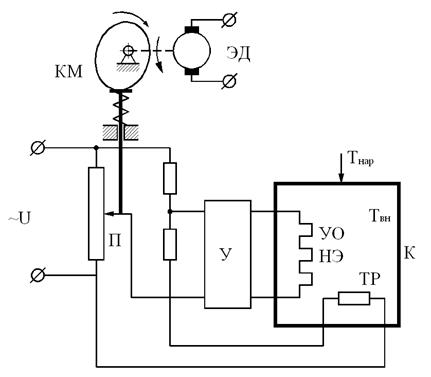
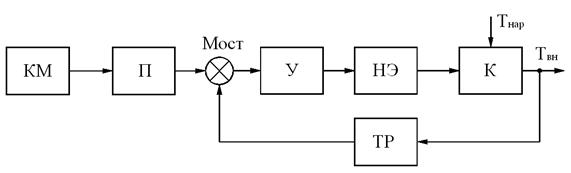
Рис. 2.16. Программная САР температуры

Точность задания программы с помощью кулачков соответствует 0,1…0,5 % (относительная погрешность). При более высоких требованиях используют электрические функциональные преобразователи; наибольшая точность достигается при использовании функциональных преобразователей дискретного типа.

Следящие системы

Это система, алгоритм которой содержит предписание изменять регулируемую величину по неизвестному заранее закону.

В зависимости от физической природы различают:

– системы воспроизводства угла;

– частоты вращения;

– момента;

– электрических величин;

Во всех перечисленных случаях входная величина может быть различной. Чаще всего используют воздействие g(t) в виде напряжения или угла поворота.

Следящие системы воспроизведения угла предназначены для поворота некоторой оси (исполнительной) по закону, определяемой другой командной осью.

Такая ситуация используется при дистанционном измерении различных величин, в автоматических потенциометрах, самопишущих приборах. По принципу действия системы практически не отличаются от стабилизирующих и программных и представляют собой замкнутые САР. В следящих системах роль задающего устройства выполняет либо человек-оператор, либо отдельные устройства.

Регулируемый объект в явном виде отсутствует. В следящих системах воспроизведения угла поворота угол поворота исполнительной оси часто отдельно не измеряется, а используются так называемые датчики рассогласования. Эти датчики вырабатывают электрический сигнал, пропорциональный углу рассогласования системы (рис. 2.17).

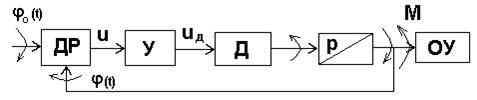
Рис. 2.17. Следящая САР угла поворота

В качестве датчиков рассогласования используют: механический дифференциал, потенциометрические датчики, вращающиеся трансформаторы, сельсинные пары.

Рассмотрим систему на потенциометрических датчиках (рис. 2.18).

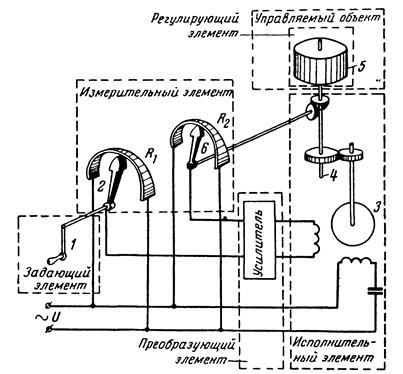
Рис. 2.18. Следящая САР на потенциометрах

Если движок R₁ повернуть на α₁ ¹ α₂, то на входе усилителя появится сигнал рассогласования, который усиливается, и двигатель через редуктор компенсирует это рассогласование, перемещая движок потенциометра R₂ на такой же угол.

Такая же система применяется в автоматических потенциометрах для измерения ЭДС (рис. 2.19).

Рис. 2.19. Автоматический потенциометр

ТП – термопара; УПТ – усилительно-преобразующий элемент.

Для контура с напряжениями Uк, Ех и Uвх: Uвх = Ех – Uк

Система должна отслеживать изменения Ех с термопары. Если Ех ¹ Uк, то имеем напряжение на двигателе, и вал двигателя перемещает движок потенциометра в сторону возникшего рассогласования, а так как с движком потенциометра связано и перо, то на бумаге получим отметку величины рассогласования системы.

Такая же система применяется в автоматических потенциометрах для измерения сопротивления. В этом случае вместо термопары устанавливается терморезистор, а в качестве сравнивающего устройства используется мостовая схема (рис. 2.20).

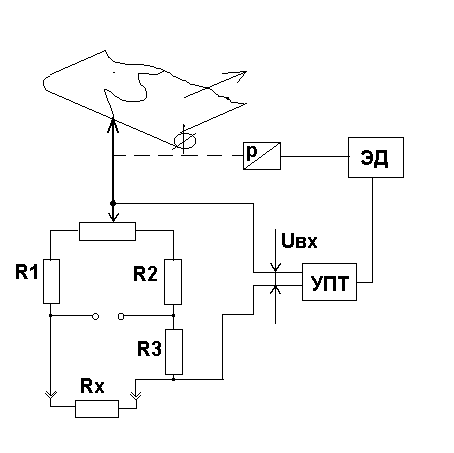
Рис. 2.20. Автомаитческий потенциометр

Следящие системы с механическим дифференциалом

Здесь в качестве датчика угла рассогласования используется механический дифференциал (рис. 2.21).

Рис. 2.21.САР угла поворота с механическим дифференциалом

Следящие системы на сельсинах и вращающихся трансформаторах (синхронные передачи)

В дистанционных САУ для передачи данных об углах поворота вала используются сельсины.

Сельсин (англ. selsуп = sеlf + sупсhгоnizing – самосинхронизирующийся) – электрическая машина, имеющая на статоре (роторе) смещенные в пространстве на 120° и соединенные звездой три обмотки, называемые обмоткой синхронизации, или трехфазной обмоткой, а на роторе (статоре) – однофазную обмотку. Сельсины предназначены:

2 для осуществления поворотов или синхронного вращения малонагруженного исполнительного вала от механически не связанного с ним командного вала, т. е. в дистанционных системах управления, для передачи на расстояние угловых перемещений или синхронного вращения;

2 для использования в качестве датчиков угла поворота в системах автоматики, для преобразования угла рассогласования двух механически не связанных валов в электрическую величину.

Простота устройства, однотипность датчика и приемника, способность к самосинхронизации, малая погрешность, устойчивость работы при колебаниях напряжения в сети питания относятся к основным преимуществам систем синхронной связи на сельсинах.

По конструктивному исполнению сельсины подразделяются на контактные и бесконтактные.

Основным в конструкции любого сельсина является равномерное распределение трех обмоток синхронизации по окружности статора или ротора и смещение их осей относительно друг друга на 120°. Это необходимо для того, чтобы результирующий магнитный поток обмотки синхронизация, равный геометрической сумме потоков трех обмоток, мог поворачиваться относительно статора (ротора) при перераспределении токов между тремя обмотками.

Большой недостаток контактных сельсинов – наличие контактных колец и щеток, которые увеличивают момент трения, уменьшают точность работы и ухудшают надежность. Указанные недостатки устранены в бесконтактных сельсинах.

В системах автоматики используются две принципиально отличающиеся системы синхронной передачи угла: индикаторная и трансформаторная.

Индикаторная система синхронной связи применяется там, где момент сопротивления на ведомой оси отсутствует или ось нагружена шкалой или стрелкой. Здесь сельсин-приемник самостоятельно отрабатывает угол, задаваемый сельсином-датчиком.

Трансформаторная система синхронной связи применяется там, где на ведомой оси имеется значительный момент сопротивления. Сельсин-приемник отрабатывает угол с помощью механически связанного с ним двигателя.

Простейшая индикаторная система синхронной связи для дистанционной "передачи угла" состоит как минимум из двух сельсинов. Сельсины соединяются по схеме приведенной на рис. 2.22. В индикаторном режиме однофазные обмотки обоих сельсинов являются первичными или обмотками возбуждения. Сельсин, вал ротора которого является командным, называется сельсин-датчик (СД). Сельсин, вал которого является исполнительными называется сельсин-приемник (СП). Углы a₁, a₂ есть отклонения осей обмоток ротора СД и СП от вертикали или от оси обмоток Е_д1 и Е_п1 соответственно статоров СД и СП.

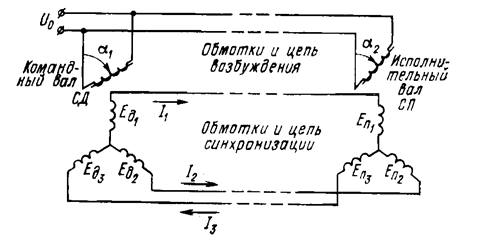
Рис. 2.22. Индикаторная схема синхронной связи

Обмотки возбуждения СД и СП подключаются к сети переменного тока. Концы одноименных фаз соединяются между собой. Намагничивающая сила, создаваемая обмотками возбуждения, имеет синусоидальное распределение по окружности ротора (статора). Тогда пульсирующий с частотой сети поток возбуждения СД и СП наведет в обмотках синхронизации синфазные ЭДС, отличающиеся по амплитуде:

ЕД1 = Еcosα1,		EП1 = Еcosα2,
EД2 = Еcos(α1 – 120o),		EП2 = Еcos(α2 – 120o),
EД3 = Еcos(α1 + 120o),		EП3 = Еcos(α1 + 120o),

откудаследует, что при a₁ = a₂, Е_дj = Е_пj (j = 1, 2, 3) токи в линиях связи отсутствуют и система находится в покое. Такое расположение роторов сельсинов называется согласованным. Появление угла рассогласования

q = a_д – a_п ¹ 0

вызовет токи в цепи синхронизации (см. рис.3):

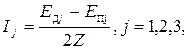
где Z – полное сопротивление одной из трех обмоток синхронизации. Токи I_j вызовут пульсирующие потоки в обмотках синхронизации, которые, взаимодействуя с потоками возбуждения, создают так называемый синхронизирующий момент, стремящийся уменьшить угол рассогласования q. Следует отметить, что одинаковый по величине, но противоположный по направлению синхронизирующий момент возникает как в сельсине-датчике, так и в сельсине-приемнике. Следовательно, если все обмотки СД и СП соединены правильно, при вращении ротора СД ротор СП будет вращаться в ту же сторону.

Сельсины в индикаторном режиме часто применяются для визуального снятия показаний стрелки, закрепленной на валу СП. Сельсинная пара в этом случае является указателем или индикатором (отсюда происхождение названия режима) относительного положения удаленных от мест наблюдения предметов: телекамеры, кинокамеры, поворота антенн, ворот шлюза и т. д.

При малых углах рассогласования (до 10°…15°) синхронизирующий момент практически пропорционален синусу угла рассогласования:

Мс(q) = Мс.max.sinq

(1)

где М_с – синхронизирующий момент; М_{с max} – максимальный синхронизирующий момент; a_д – угол поворота ротора сельсина датчика; a_п – угол поворота сельсина приемника.

М_с(0) = М_с(180) = 0, но положение сельсинов при q = 180° является неустойчивым. Благодаря этому, сельсинная пара в индикаторном режиме обеспечивает синхронизацию угла в пределах одного оборота. Величина

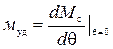(2)

называется удельным синхронизирующим моментом, который может определяться экспериментально из снятой кривой М_с(q).

На основании формул (1) и (2) легко получить выражение, справедливое с точностью до 1%.

М_с(q) = М_удq,

– 0,24 рад £ q £ 0,24 рад

Если на валу СП имеется момент нагрузки М_н, то процесс синхронизации будет всегда заканчиваться при

М_с = М_н = М_удq = М_уд(a₁ – a₂),

откуда

a2=a1 – Dq,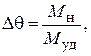

(3)

где Δq – абсолютная статическая ошибка сельсинного датчика, которая для одного и того же М_н тем меньше, чем больше М_уд.

Точность отработки угла сельсинов-приемников характеризуется статической ошибкой. Величину статической ошибки сельсинной пары в индикаторном режиме принято характеризовать средней максимальной ошибкой Dq_m, которая определяется как полусумма абсолютных значений максимальных ошибок для двух противоположных направлений вращения в пределах одного оборота.

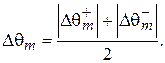
Погрешность в статическом режиме определяется путем поворота ротора датчика сначала по часовой стрелке на 360°, а затем против часовой тоже на 360°. Измерения производят либо непрерывно с помощью приборов, либо через 1° или через 10° в зависимости от требуемой точности определения погрешности.

Точность работы сельсинов-приемников в индикаторном режиме определяют следующие основные факторы:

2 момент сопротивления, у большинства сельсинов он равен моменту трения М_т;

2 добротность сельсина:

Д = М_уд/М_т;

– магнитная несимметрия – неравенство магнитных сопротивлений на пути его потока возбуждения при разных положения ротора;

– электрическая несимметрия – неравенство сопротивлений фаз обмоток синхронизации се