Пропускная способность каналов связи.
Для описания каналов связи используется характеристика средней скорости передачи информации в единицу времени с заданной верностью. Существует максимально возможная (предельная) скорость передачи, которая называется пропускной способностью канала С. Это фундаментальное понятие определяет потенциальные возможности системы связи, использующей данный канал. В реальной системе средняя скорость передачи информации всегда меньше пропускной способности канала. В теории информации К. Шенноном доказана теорема, согласно которой для источника без избыточности при скорости передачи меньшей, чем пропускная способность канала можно найти такой способ кодирования-декодирования, при котором возможна передача сообщений по каналу с помехами со сколь угодно малой ошибкой.
Любая физическая среда характеризуется фундаментальными ограничениями по максимальной скорости передачи информации. Этот предел - предел Шеннона - определяется двумя параметрами: полосой пропускания и соотношением сигнал/ шум. Полоса пропускания линии - это разность максимальной (верхней) и минимальной (нижней) частот сигнала, способного распространяться в линии связи. Соотношение сигнал/ шум это характеристика не столько самой линии связи, сколько системы "передатчик + канал связи + приемник". Поэтому при описании линий связи пользуются такими характеристиками, как коэффициент затухания сигнала на единицу длины линии и уровень помех (шумов).
Предел Шеннона.
Количество информации, передаваемой без искажений в единицу времени, ограничено емкостью канала (не электрической). Информационная емкость (пропускная способность) канала в случае его поражения белым (гауссовым) шумом 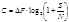 (бит/сек),
(бит/сек),
где DF - передаваемая полоса частот, S - средняя мощность сигнала, N - средняя мощность шума.
Мощности сигнала и шума имеют естественные физические ограничения. Мощность сигнала связана с параметрами передатчика. Снижение уровня шума требует применения дорогих линий связи с эффективным экранированием и малошумящей аппаратуры. Влияние мощностей на пропускную способность канала связи определяется логарифмической зависимостью. Так, при исходном отношении сигнал/шум =100 (типичный случай) повышение мощности передатчика в 2 раза даст около 15% увеличения пропускной способности канала связи.
Соотношение Найквиста.
Аналогичным пределу Шеннона является соотношение Найквиста, которое также определяет пропускную способность канала, но без учета шумов:
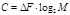
где М- количество различимых состояний информационного параметра.
Если для кодирования используется более двух состояний, то пропускная способность линии повышается, т.к. за один такт работы передатчика передается несколько бит данных. Например, слово из нескольких бит можно кодировать в одном такте одновременным изменением комбинации фазы и амплитуды.
Число изменений информационного параметра несущего сигнала в секунду измеряется в бодах (baud). Жан Эмиль Бодо (Франция) создал телеграфный аппарат в 1874г., конструкция которого практически без изменений использовалась более 100 лет. Пропускная способность канала связи в битах в секунду в общем случае не совпадает с числом бод.
Если сигнал имеет более двух различимых состояний, то пропускная способность в битах/сек будет выше числа бод. Например, если информационными параметрами являются фаза и амплитуда синусоиды, причем различаются 4 состояния фазы (0, 90, 180 и 2700) и два значения амплитуды, то информационный сигнал может иметь 8 различимых состояния. В этом случае модем, работающий со скоростью 2400 бод (несущая частота 2400Гц) передает информацию со скоростью 7200 бит/сек, т.к. при одном изменении сигнала передается 3 бита информации (8=23).
Преобразования сигнала в каналах связи.Кодирование и модуляция
Преобразование первичного информационного сигнала в высокочастотный сигнал необходимо для согласования сигнала с каналом, т.е. реализации условияVC£VK.
Преобразование дискретного сообщения в сигнал осуществляется в виде кодирования и модуляции. В простейшем случае сигнал согласуют с каналом по всем трём параметрам, т.е. добиваются выполнения условий:Tс<TkFс<FkDс<Dс
При этом объём сигнала полностью "вписывается" в объём канала.
Однако условие согласования канала может выполняться и тогда, когда одно или два из частичных неравенств не выполнены. Это означает, что можно производить "обмен" длительности на ширину спектра или ширину спектра на динамический диапазон и т.д. Пусть, например, записанный на плёнку телефонный сигнал, имеющий ширину спектра 3 кГц, необходимо передать через канал, полоса пропускания которого 300 Гц. Это можно осуществить, воспроизводя сигнал со скоростью, в 10 раз меньше той, с которой он был записан. При этом все частоты исходного сигнала уменьшатся в 10 раз, и во столько же раз увеличится время передачи. Принятый сигнал также записывается на плёнку, а затем, воспроизведя его со скоростью, в 10 раз большей, можно восстановить исходный сигнал Аналогично можно передать сигнал быстрее, если полоса пропускания канала шире спектра сигнала.
Значительно больший интерес представляет возможность обмена динамического диапазона на полосу пропускания. Так, используя широкополосные помехоустойчивые виды модуляции, можно передать сообщение с динамическим диапазоном, например 60 дБ, по каналу, в котором сигнал превышает помеху всего лишь на 20 дБ. Но при этом используется полоса пропускания канала в несколько раз более широкая, чем спектр сообщения.
Преобразование дискретного сообщения в сигнал обычно осуществляется в виде двух операций - кодирования и модуляции. Кодирование – преобразование сообщения в последовательность кодовых символов, а модуляция – преобразование этих символов в сигналы, пригодные для передачи по каналу. С помощью кодирования и модуляции источник сообщений согласуется с каналом.
Простейшим примером дискретного сообщения является текст. Любое сообщение состоит из конечного числа элементов; текст – из букв, цифр, знаков препинания. Их совокупность называется алфавитом источника сообщения. Так как число элементов в алфавите конечно, то их можно пронумеровать и тем самым свести передачу сообщения к передаче последовательности чисел. Обычно моменты отсчётов выбираются на оси времени равномерно.
Квантование - представление бесконечного множества значений, которое может принимать аналоговый сигнал, набором ограниченного множества.

Операция квантования сводится к тому, что вместо данного мгновенного значения (уровня) передаваемого сообщения передают ближайшие значения по установленной цифровой шкале дискретных уровней. Дискретные значения по шкале уровней чаще всего выбираются равномерно. Само собой разумеется, что при квантовании вносится погрешность, так как истинное значение заменяют округлённым значением. Величина этой погрешности при равномерном квантовании не превосходит половины шага квантования и может быть сведена до допустимого уровня.
Дискретизированныйсигнал принимает отличные от нуля значения только в определенные моменты времени. Дискретизированный сигнал может быть получен как из исходного непрерывного, так и из квантованного сигнала.
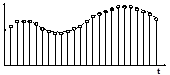
Дискретизация по времени позволяет преобразовать непрерывные сообщения в дискретный (во времени) сигнал, который после квантования превращается в цифровой. Достоинством цифровых способов передачи является возможность применения кодов, как для повышения помехоустойчивости, так и для сокращения избыточности источника.
В настоящее время широкое применяется система с импульсно - кодовой модуляцией (ИКМ). В этой системе непрерывное сообщение сначала подвергается дискретизации по времени и квантованию по уровню, а затем полученная последовательность уровней (цифр) кодируется (обычно двоичным кодом). Каждому уровню присваивается кодовая комбинация, состоящая из п символов 1 или 0. Полученная последовательность двоичных символов передаётся по каналу связи одним из методов дискретной модуляции. Весовые коэффициенты 0 и 1 и могут передаваться отрезками колебаний различных частот, отрезками колебаний с отличающимися начальными фазами или постоянным током с разной амплитудой или полярностью. Это обеспечивает простоту аппаратуры.
Рассмотрим источник дискретного сообщения. Пусть сообщение выражено при помощи некоторых символов, например, букв печатного текста. Если далее эти буквы преобразуются в другие символы или последовательности из них по заранее установленному и известному при передаче и приеме правилу, то говорят, что сообщение дискретного источника кодируется.
Набор символов (букв), над которым определена последовательность символов на выходе дискретного источника, называется алфавитом. Число символов в алфавите называется объемом алфавита.
Отрезок кодовой последовательности (комбинации) называется блоком. Число символов (элементов) в блоке называется значностью или длиной блока.
Блок, выделенный по определенному признаку и рассматриваемый как одно целое, называется информационным словом. Словом, например, является кодовая последовательность (комбинация). Совокупность (множество) всех кодовых комбинаций, возможных при заданном правиле кодирования, образует код.
Блоки системы связи, в которых осуществляется кодирование, называются кодерами.
Коды, у которых все кодовые комбинации имеют одинаковую длину, называются равномерными. Неравномерные коды содержат кодовые комбинации неравной длины. Равномерное кодирование характеризуется простотой алгоритмов и аппаратуры кодеков и декодеров; неравномерное кодирование отличается большей эффективностью.
Одной из задач кодирования является задача согласования алфавита, из которого построены дискретные сообщения с кодовым алфавитом выходных комбинаций.
Кодирование позволяет решить также задачу устранения избыточности источника сообщения и тем самым повысить скорость передаваемой информации. Примерами кодов, решающими эту задачу (задачу эффективного кодирования), являются коды Шеннона- Фано и Хаффмена. Эти коды являются неравномерными. Для повышения достоверности передачи дискретной информации применяют помехоустойчивые коды. В отличие от простых, у которых все возможные кодовые комбинации используются для передачи информации, помехоустойчивые коды строятся так, что для передачи используется лишь часть от общего числа возможных комбинации. Благодаря этому появляется возможность обнаруживать и исправлять ошибки. Способность кода обнаруживать и исправлять ошибки достигается также и тем, что, наряду с информационными, по каналу связи передаются проверочные символы.
