Понятие корреляционной зависимости и ее направленности
Будем говорить, что между двумя признаками Х и У существует корреляционная зависимость (взаимосвязь), при которой с изменением одного признака изменяется и другой, но каждому значению признака Х могут соответствовать разные, заранее непредсказуемые значения признака У, и наоборот.
Для различия направленности влияния одного признака на другой введены понятия положительной и отрицательной связи.
Если с увеличением (уменьшением) одного признака в основном увеличиваются (уменьшаются) значения другого, то такая корреляционная связь называется прямой или положительной.
Если с увеличением (уменьшением) одного признака в основном уменьшаются (увеличиваются) значения другого, то такая корреляционная связь называется обратной или отрицательной.
2. Корреляционные поля и их использование в предварительном анализе корреляционной связи
При постановке вопроса о корреляционной зависимости между двумя статистическими признаками Х и У проводят эксперимент с параллельной регистрацией их значений.
Пример 8.1.
Определить, зависит ли результат прыжка в длину с разбега (признак Х) от величины конечной скорости разбега (признак У). Для ответа на этот вопрос параллельно с регистрацией результата Х каждого прыжка спортсмена или группы спортсменов регистрируют и величину конечной скорости разбега Y . Пусть они таковы:
Таблица 5
| I | ||||||||
| xi ( см ) | ||||||||
| yi ( м/с ) | 10,7 | 10,5 | 10,1 | 9,8 | 10,1 | 10,5 | 9,1 | 9,6 |
Представим таблицу 5 в виде графика в прямоугольной системе координат, где на горизонтальной оси будем откладывать длину прыжка (Х), а на вертикальной — величину конечной скорости разбега в этом прыжке ( Y ).
function PlayMyFlash(cmd){ Corel_.TPlay(cmd); } 
№1 !!! №2 !!! №3 !!! №4 !!! №5!!! №6 !!! №7 !!! №8!!!
Рис. 8. График корреляционного поля.
Будем называть корреляционным полем зону разброса таким образом полученных точек на графике. Визуально анализируя корреляционное поле на рисунке 8, можно заметить, что оно как бы вытянуто вдоль какой-либо прямой линии. Такая картина характерна для так называемой линейной корреляционной взаимосвязи между признаками. При этом можно в общем предположить, что с увеличением конечной скорости разбега увеличивается и длина прыжка, и наоборот. Т.е. между рассматриваемыми признаками наблюдается прямая (положительная) взаимосвязь.
Наряду с этим примером из множества других возможных корреляционных полей можно выделить следующие (рис.9-11):
На рисунке 9 тоже просматривается линейная взаимосвязь, но с увеличением значений одного признака, уменьшаются значения другого, и наоборот, т.е. связь обратная или отрицательная. Можно предположить, что на рисунке 11 точки корреляционного поля разбросаны около какой-то кривой линии. В таком случае говорят, что между признаками существует криволинейная корреляционная связь.
В отношении корреляционного поля, изображенного на рисунке 10, нельзя сказать, что точки располагаются вдоль какой-то прямой или кривой линии, оно имеет сферическую форму. В этом случае говорят, что признаки Х и Y не зависят друг от друга.
Кроме этого по корреляционному полю можно примерно судить о тесноте корреляционной связи, если эта связь существует. Здесь говорят: чем меньше точки разбросаны около воображаемой усредненной линии, тем теснее корреляционная связь между рассматриваемыми признаками.
Визуальный анализ корреляционных полей помогает разобраться в сущности корреляционной взаимосвязи, позволяет высказать предположение о наличии, направленности и тесноте связи. Но точно сказать, имеется связь между признаками или нет, линейная связь или криволинейная, тесная связь (достоверная) или слабая (недостоверная), с помощью этого метода нельзя. Наиболее точным методом выявления и оценки линейной взаимосвязи между признаками является метод определения различных корреляционных показателей по статистическим данным.
3. Коэффициенты корреляции и их свойства
Часто для определения достоверности взаимосвязи между двумя признаками(Х, У) используютнепараметрический (ранговый) коэффициент корреляции Спирмена 
и параметрический коэффициент корреляции Пирсона 
. Величина этих показателей корреляционной связи определяется по следующим формулам:
(1)
где: dx — ранги статистических данных признака х;
dy — ранги статистических данных признака у.
(2)
где: 
— статистические данные признака х,
— статистические данные признака у.
Эти коэффициенты обладают такими мощными признаками:
1. На основании коэффициентов корреляции можно судить только о прямолинейной корреляционной взаимосвязи между признаками. О криволинейной связи с их помощью ничего сказать нельзя.
2. Значения коэффициентов корреляции есть безразмерная величина, которая не может быть меньше -1 и больше +1, т.е.
3. 
4. Если значения коэффициентов корреляции равны нулю, т.е. 
= 0 или 
= 0, то связь между признаками х, у отсутствует.
5. Если значения коэффициентов корреляции отрицательные, т.е. < 0 или < 0, то связь между признаками Х и Y обратная.
6. Если значения коэффициентов корреляции положительные, т.е. > 0 или y> 0 , то связь между признаками Х и Y прямая (положительная).
7. Если коэффициенты корреляции принимают значения +1 или -1, т.е. = ± 1 или = ± 1, то связь между признаками Х и Y линейная (функциональная).
8. Только по величине коэффициентов корреляции нельзя судить о достоверности корреляционной связи между признаками. Эта достоверность еще зависит от числа степеней свободы.
k = n - 2, (3)
где: n — число коррелируемых пар статистических данных признаков Х и Y.
Чем больше n , тем выше достоверность связи при одном и том же коэффициенте корреляции.
Кроме перечисленных общих свойств у рассматриваемых коэффициентов корреляции имеются и различия. Главное их отличие состоит в том, что коэффициент Пирсона ( 
может быть использован только в случае нормальности распределения признаков Х и Y , коэффициент Спирмена ( ) может быть использован для признаков с любым видом распределения. Если рассматриваемые признаки имеют нормальное распределение, то целесообразнее определять наличие корреляционной связи с помощью коэффициента Пирсона ( ), т.к. в этом случае он будет иметь меньшую погрешность, чем коэффициент Спирмена ( ).
Пример 8.2.
Определить с помощью рангового коэффициента корреляции Спирмена существует ли взаимосвязь между результатами прыжка в длину с разбега (X) и конечной скоростью разбега (Y) группы спортсменов (данные примера 8.1, табл. 5).
В формуле (1) dx и dy ранги статистических данных, т.е. места вариант в их ранжированной совокупности. Если в совокупности несколько одинаковых данных, то их ранги равны и определяются как среднее значение от мест, занимаемых этими вариантами. Например,
| Данные xi | |||||||||
| Ранги dx | 4,5 | 4,5 | 4,5 | 4,5 | 7,5 | 7,5 |
| 3 + 4 + 5 + 6 | 7 + 8 | |||
Пользуясь этим правилом, определим ранги данных таблицы 5. Для удобства все запишем в виде таблицы 6.
Таблица 6
| | dx | | dy | dx - dy |  |
| 9,1 | 1 - 1 = 0 | 02 = 0 | |||
| 9,6 | 2 - 2 = 0 | 02 = 0 | |||
| 9,8 | 3 - 3 = 0 | 02 = 0 | |||
| 10,1 | 4 - 4 = 0 | 02 = 0 | |||
| 10,5 | 6,5 | 5 - 6,5 = - 1,5 | (- 1,5)2 = 2,25 | ||
| 10,5 | 6,5 | 6 - 6,5 = - 0,5 | (- 0,5)2 = 0,25 | ||
| 10,3 | 7 - 5 = 2 | 22 = 4 | |||
| 10,7 | 8 - 8 = 0 | 02 = 0 | |||
 (dx-dy) = 0 |  |
В данном случае имеем 8 пар значений, т.е. 8 коррелируемых пар. Значит n = 8. Подставив полученное в формулу (1), будем иметь:
Вывод:
а) т.к. значение коэффициента корреляции положительное (0,92 > 0), то между признаками Х и Унаблюдается прямая связь, т.е. с увеличением скорости разбега (признак У) увеличивается длина прыжка (признак Х), и наоборот — с уменьшением скорости разбега уменьшается длина прыжка. Достоверность коэффициента корреляции Спирмена определяется по таблице критических значений рангового коэффициента корреляции 
.
б) т.к. полученное значение коэффициента корреляции = 0,9 больше табличного значений = 0,88, соответствующего уровню b = 99%, то уверенность в правильности вывода (а) больше 99%. Такая достоверность позволяет распространить вывод (а) на всю генеральную совокупность, т.е. на всех прыгунов в длину.
Если не производится предварительной проверки рассматриваемых совокупностей на нормальность распределения, то , в случае недостоверности коэффициента корреляции Пирсона, следует проверить наличие связи еще и по коэффициенту Спирмена.
Пример 8.3.
Ранговым коэффициентом корреляции можно выявлять взаимосвязи между переменными, имеющими любые статистические распределения. Но если эти переменные имеют нормальное распределение (Гаусса), то более точно связь можно установить с помощью нормированного (Бравэ-Пирсона) коэффициента корреляции.
Предположим, что в нашем примере и — отвечают закону нормального распределения, и проверим наличие связи между результатами тестаX и Y c помощью расчета нормированного коэффициента корреляции.
Из формулы (1) видно, что для вычисления необходимо найти средние значения признаковX, Y и отклонения каждого статистического данного от его среднего 
. Зная эти значения, можно найти суммы 
по которым не сложно вычислить
По данным таблице 5 заполним таблицу 7:
Таблица 7
| |  |  | |  |  |  |
| 962 = 9216 | 10,7 | 0,6 | 0,62 = 0,36 | 96 · 0,6 = 57,6 | ||
| 262 = 676 | 10,5 | 0,4 | 0,42 = 0,16 | 26 · 0,4 = 10,4 | ||
| 10,3 | 0,2 | 0,04 | 5,4 | |||
| - 4 | 9,8 | - 0,3 | 0,09 | 1,2 | ||
| 10,1 | 0,00 | 1,0 | ||||
| 10,5 | 0,4 | 0,16 | 3,2 | |||
| - 92 | 9,1 | - 1,0 | 1,00 | 9,2 | ||
| - 64 | 9,6 | - 0,5 | 0,25 | 32,0 | ||
 |  = 23262 |  | = 2,06 | = 201 |
Подставив сумму столбца 7 в числитель формулы (1), а суммы столбцов 3 и 6 в знаменатель, получим:
Вывод:
а) т.к. значение коэффициента корреляции положительное (0.92>0), то между Х и Yнаблюдается прямая связь, т.е. с увеличением скорости разбега (признакY) увеличивается длина прыжка (признак Х) и наоборот — с уменьшением скорости разбега уменьшается длина прыжка. Очень важно знать уверенность в правильности полученного вывода.
Для этого по таблице критических значений нормированного коэффициента корреляции определим достоверность найденного коэффициента корреляции. Здесь число степеней свободы согласно формуле (3) будет:
k = n - 2 = 8 - 2 = 6.
По таблице критических значений нормированного коэффициента корреляции для k = 6 величина 
= 0,71 соответствует уверенности в 95% ( b = 100% - a ), а 
= 0,83 соответствует уверенности в 99%;
б) т.к. полученное значение коэффициента корреляции = 0,94 больше табличного значения = 0,83, соответствующего уровню 
= 99%, то уверенность в правильности вывода (а) больше 99%. В области спорта такая уверенность достаточна, поэтому полученный вывод (а) можно распространять на всю генеральную совокупность (на всех прыгунов в длину).
Ход работы
ЗАДАЧА 1.
По результатам тестирования группы по ОФП определить визуально с помощью корреляционного поля существует ли взаимосвязь между показателями индекса Кетле (Х) и становой силы (Y) у студентов группы __________________ (n=7) , если данные таковы:
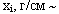
Решение:
Представим данные тестирования в виде графика в прямоугольной системе координат:
Вывод:
ЗАДАЧА 2.
Определить наличие взаимосвязи между показателями индекса Кетле (X) и становой силы (Y) у студентов группы _________ с помощью расчета рангового коэффициента корреляции Спирмена.
Решение:
1. Занести результаты тестирования в рабочую таблицу и сделать соответствующие расчеты: 
2. Рассчитать ранговый коэффициент корреляции по формуле:
.
Вывод:
ЗАДАЧА 3.
Определить наличие взаимосвязи между показателями индекса Кетле(Х) и становой силы (Y ) у студентов группы ________ с помощью расчета нормированного коэффициента корреляции Бравэ-Пирсона.
Решение:
2. Занести результаты тестирования в рабочую таблицу и сделать соответствующие расчеты:
2 . Рассчитать нормированный коэффициент корреляции по формуле:
k = n – 2 =
Вывод:
Контрольные вопросы
1. Какая связь между переменными называется функциональной? Привести ее пример из области спорта и физической культуры.
2. Какая взаимосвязь между признаками называется статистической? Привести примеры.
3. Какая связь между переменными называется корреляционной? Пояснить примерами.
4. Цель применения корреляционного анализа.
5. Корреляционные поля и цель их построения.
6. Перечислить и пояснить на примерах свойства коэффициентов корреляции.
7. В чем отличие расчета рангового коэффициента корреляции от нормированного?