Тема 1. основы теории измерений

ПРЕДМЕТ СПОРТИВНОЙ МЕТРОЛОГИИ

Слово "метрология" в переводе с древнегреческого означает "наука об измерениях" (метрон — мера, логос — слово, наука).
Основной задачей общей метрологии является обеспечение единства и точности измерений. Спортивная метрология как научная дисциплина представляет собой часть общей метрологии. К ее основным задачам относятся:

1. Разработка новых средств и методов измерений.
2. Регистрация изменений в состоянии занимающихся под влиянием различных физических нагрузок.
3. Сбор массовых данных, формирование систем оценок и норм.
4. Обработка полученных результатов измерений с целью организации эффективного контроля и управления учебно-тренировочным процессом.

Однако как учебная дисциплина спортивная метрология выходит за рамки общей метрологии. Так, в физическом воспитании и спорте помимо обеспечения измерения физических величин, таких как длина, масса и т.д., подлежат измерению педагогические, психологические, биологические и социальные показатели, которые по своему содержанию нельзя назвать физическими. Методикой их измерений общая метрология не занимается и, поэтому, были разработаны специальные измерения, результаты которых всесторонне характеризуют подготовленность физкультурников и спортсменов.
Использование методов математической статистики в спортивной метрологии дало возможность получить более точное представление об измеряемых объектах, сравнить их и оценить результаты измерений.
В практике физического воспитания и спорта проводят измерения в процессе систематического контроля (фр. проверка чего-либо), в ходе которого регистрируются различные показатели соревновательной и тренировочной деятельности, а также состояние спортсменов. Такой контроль называют комплексным.
Это дает возможность установить причинно-следственные связи между нагрузками и результатами в соревнованиях. А после сопоставления и анализа разработать программу и план подготовки спортсменов.
Таким образом, предметом спортивной метрологии является комплексный контроль в физическом воспитании и спорте и использование его результатов в планировании подготовки спортсменов и физкультурников.
Систематический контроль за спортсменами позволяет определить меру их стабильности и учитывать возможные погрешности измерений.

Тема: Основы теории измерений
Цель:научиться осуществлять корректную постановку задач измерения,
выбирать единицы, средства и методы измерения, определять их точность.

Теоретические сведения

Измерением (в широком смысле слова) называют установление соответствия между изучаемыми явлениями, с одной стороны, и числами, с другой.
Чтобы результаты разных измерений можно было сравнивать друг с другом, они должны быть выражены в одних и тех же единицах. В 1960 г. на Международной генеральной конференции по мерам и весам была принята Международная система единиц, получившая сокращенное название СИ.
СИ в настоящее время включает семь независимых друг от друга основных единиц, из которых в качестве производных выводят единицы остальных физических величин. Производные единицы определяются на основе формул, связывающих между собой физические величины.
Например, единица длины (метр) и единица времени (секунда) — основные единицы, а единица скорости (метр за секунду [м/с]) — производная. Совокупность выбранных основных и образованных с их помощью производных единиц для одной или нескольких областей измерения называется системой единиц (табл. 1).

Таблица 1

Основные единицы СИ

Единица

Величина

Размерность

Название

Обозначение

			русское	международное
Длина	L	Метр	м	m
Масса	M	Килограмм	кг	kg
Время	T	Секунда	с	S
Сила эл. тока	I	Ампер	А	A
Температура	q	Кельвин	К	K
Кол-во вещ-ва	N	Моль	моль	mol
Сила света	G	Канделла	Кд	cd

Для образования кратных и дольных единиц должны использоваться специальные приставки (табл. 2).

Таблица 2

Множители и приставки

Множители

Приставка

1 000 000=106	Мега	М
1 000=103	Кило	к
100=102	Гекто	Г
10=101	Дека	Д
0,1=10-1	деци	d
0,01=10-2	санти	с
0,001=10-3	милли	m
0,000 001=10-6	микро	m

Все производные величины имеют свои размерности.
Размерностью называется выражение, связывающее производную величину с основными величинами системы при коэффициенте пропорциональности, равном единице. Например, размерность скорости равна 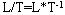, а размерность ускорения равна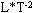
Никакое измерение не может быть выполнено абсолютно точно. Результат измерения неизбежно содержит погрешность, величина которой тем меньше, чем точнее метод измерения и измерительный прибор.
Основная погрешность —это погрешность метода измерения или измерительного прибора, которая имеет место в нормальных условиях их применения.
Дополнительная погрешность —это погрешность измерительного прибора, вызванная отклонением условий его работы от нормальных.
Величина D А=А-А0, равная разности между показанием измерительного прибора (А) и истинным значением измеряемой величины (А0), называется абсолютной погрешностьюизмерения. Она измеряется в тех же единицах, что и сама измеряемая величина.
Относительная погрешность —это отношение абсолютной погрешности к значению измеряемой величины:

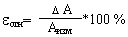
В тех случаях, когда оценивается не погрешность измерения, а погрешность измерительного прибора, за максимальное значение измеряемой величины принимают предельное значение шкалы прибора. В таком понимании наибольшее допустимое значение D Па, выраженное в процентах, определяет в нормальных условиях работы класс точности измерительного прибора.
Систематическойназывается погрешность, величина которой не меняется от измерения к измерению. В силу этой своей особенности систематическая погрешность часто может быть предсказана заранее или в крайнем случае обнаружена и устранена по окончании процесса измерения.
Тарированием (от нем. tarieren) называется проверка показаний измерительных приборов путем сравнения с показаниями образцовых значений мер (эталонов* ) во всем диапазоне возможных значений измеряемой величины.
Калибровкой называется определение погрешностей или поправка для совокупности мер (например, набора динамометров). И при тарировании, и при калибровке к входу измерительной системы вместо спортсмена подключается источник эталонного сигнала известной величины. Например, тарируя установку для измерения усилий, на тензометрической платформе поочередно помещают грузы весом 10, 20, 30 и т.д. килограммов.
Рандомизацией (от англ. random — случайный) называется превращение систематической погрешности в случайную. Этот прием направлен на устранение неизвестных систематических погрешностей. По методу рандомизации измерение изучаемой величины производится несколько раз. При этом измерения организуют так, чтобы постоянный фактор, влияющий на их результат, действовал в каждом случае по-разному. Скажем, при исследовании физической работоспособности можно рекомендовать измерять ее многократно, всякий раз меняя способ задания нагрузки. По окончании всех измерений их результаты усредняются по правилам математической статистики.
Случайные погрешностивозникают под действием разнообразных факторов, которые ни предсказать заранее, ни точно учесть не удается.
Стандарт —нормативно-технический документ, устанавливающий комплекс норм, правил, требований к объекту стандартизации и утвержденный компетентным органом — Государственным комитетом по стандартизации. В спортивной метрологии объектом стандартизации являются спортивные измерения.

Шкала наименований (номинальная шкала)

Это самая простая из всех шкал. В ней числа выполняют роль ярлыков и служат для обнаружения и различения изучаемых объектов (например, нумерация игроков футбольной команды). Числа, составляющие шкалу наименований, разрешается менять местами. В этой шкале нет отношений типа "больше — меньше", поэтому некоторые полагают, что применение шкалы наименований не стоит считать измерением. При использовании шкалы наименований могут проводится только некоторые математические операции. Например, ее числа нельзя складывать и вычитать, но можно подсчитывать, сколько раз (как часто) встречается то или иное число.

Шкала порядка

Есть виды спорта, где результат спортсмена определяется только местом, занятым на соревнованиях (например, единоборства). После таких соревнований ясно, кто из спортсменов сильнее, а кто слабее. Но насколько сильнее или слабее, сказать нельзя. Если три спортсмена заняли соответственно первое, второе и третье места, то каковы их различия в спортивном мастерстве, остается неясным: второй спортсмен может быть почти равен первому, а может быть существенно слабее его и быть почти одинаковым с третьим. Места, занимаемые в шкале порядка, называются рангами, а сама шкала называется ранговой или неметрической. В такой шкале составляющие ее числа упорядочены по рангам (т.е. занимаемым местам), но интервалы между ними точно измерить нельзя. В отличие от шкалы наименований шкала порядка позволяет не только установить факт равенства или неравенства измеряемых объектов, но и определить характер неравенства в виде суждений: "больше — меньше", "лучше — хуже" и т.п.
С помощью шкал порядка можно измерять качественные, не имеющие строгой количественной меры, показатели. Особенно широко эти шкалы используются в гуманитарных науках: педагогике, психологии, социологии. К рангам шкалы порядка можно применять большее число математических операций, чем к числам шкалы наименований.

Шкала интервалов

Это такая шкала, в которой числа не только упорядочены по рангам, но и разделены определенными интервалами. Особенность, отличающая ее от описываемой дальше шкалы отношений, состоит в том, что нулевая точка выбирается произвольно. Примерами могут быть календарное время (начало летоисчисления в разных календарях устанавливалось по случайным причинам), суставной угол (угол в локтевом суставе при полном разгибании предплечья может приниматься равным либо нулю, либо 180о), температура, потенциальная энергия поднятого груза, потенциал электрического поля и др.
Результаты измерений по шкале интервалов можно обрабатывать всеми математическими методами, кроме вычисления отношений. Данные шкалы интервалов дают ответ на вопрос "на сколько больше?", но не позволяют утверждать, что одно значение измеренной величины во столько-то раз больше или меньше другого. Например, если температура повысилась с 10о до 20о по Цельсию, то нельзя сказать, что стало в два раза теплее.

Шкала отношений

Эта шкала отличается от шкалы интервалов только тем, что в ней строго определено положение нулевой точки. Благодаря этому шкала отношений не накладывает никаких ограничений на математический аппарат, используемый для обработки результатов наблюдений.
В спорте по шкале отношений измеряют расстояние, силу, скорость и десятки других переменных. По шкале отношений измеряют и те величины, которые образуются как разности чисел, отсчитанных по шкале интервалов. Так, календарное время отсчитывается по шкале интервалов, а интервалы времени — по шкале отношений.
При использовании шкалы отношений (и только в этом случае!) измерение какой-либо величины сводится к экспериментальному определению отношения этой величины к другой подобной, принятой за единицу. Измеряя длину прыжка, мы узнаем во сколько раз эта длина больше длины другого тела, принятого за единицу длины (метровой линейки в частном случае); взвешивая штангу, определяем отношение ее массы к массе другого тела — единичной гири "килограмма" и т.п. Если ограничиться только применением шкал отношений, то можно дать другое (более узкое, частное) определение измерению: измерить какую-либо величину — значит найти опытным путем ее отношение к соответствующей единице измерения.
В таблице 3 приведены сводные сведения о шкалах измерения.

Таблица 3

Шкалы измерений.

Шкала	Основные операции	Допустимые математические процедуры	Примеры
Наименований	Установление равенства	Число случаев Мода Корреляция случайных событий (тетра- и полихорические коэффициенты корреляции)	Нумерация спортсменов в команде Результаты жеребьевки
Порядка	Установление соотношений "больше" или "меньше"	Медиана Ранговая корреляция Ранговые критерии Проверка гипотез непараметрической статистикой	Место, занятое на соревнованиях Результаты ранжирования спортсменов группой экспертов
Интервалов	Установление равенства интервалов	Все методы статистики кроме определения отношений	Календарные даты (время) Суставной угол Температура тела
Отношений	Установление равенства отношений	Все методы статистики	Длина, сила, масса, скорость и т.п.

Ход работы

ЗАДАЧА 1.
Определить в единицах СИ:
а) мощность (N) электрического тока, если его напряжение U=1кВ, сила I=500 mA;
б) среднюю скорость (V) объекта, если за время t=500 мс им пройдено расстояние S=10 см;
в) силу тока (I), протекающего в проводнике с сопротивлением 20 кОм, если к нему приложено напряжение 100 мВ.
Решение:

N=U*I; N =

V=S/t; V =

I=U/R; I =

Вывод:

ЗАДАЧА 2.
Найти точное значение становой силы, если показание станового динамометра равно Fизм=140 кГ, абсолютная погрешность составляет
D F= ± 3 кГ.
Решение:

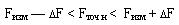Вывод:

ЗАДАЧА 3.
Определить, что измерено точнее пальпаторным методом: пульс покоя за 1 мин (р1=72 уд.) или за 10 с (р2=11 уд.), если абсолютная погрешность измерения 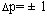уд.
Решение:

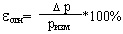e 1=

e2=

Вывод:

ЗАДАЧА 4.
Определить точное значение показателя становой силы у исследуемого, если максимальное значение шкалы станового динамометра Fmax=450 кГ, класс точности прибора КТП=1,5%, а показанный результат Fизм=210 кГ.
Решение:

или

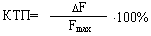
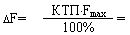
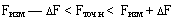
Вывод:

ЗАДАЧА 5.
Рандомизировать показания своей частоты сердечных сокращений в покое, измерив ее трижды за 15 с.
Р1= ; р2= ; р3= .
Решение:


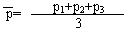
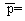
Вывод:

Контрольные вопросы

1. Предмет и задачи спортивной метрологии.
2. Понятие об измерении и единицах измерения.
3. Шкалы измерений.
4. Основные, дополнительные, производные единицы СИ.
5. Размерность производных величин.
6. Понятие о точности измерений и погрешностях.
7. Виды погрешностей (абсолютная, относительная, систематическая и случайная).
8. Понятие о классе точности прибора, тарировке, калибровке и рандомизации.